TEORIA DELLA PRODUZIONE

L’imprenditore si assume il compito di organizzare i fattori produttivi e affronta il rischio della produzione: rischio tecnico (es. guasto degli impianti) e rischio economico (es. mancata vendita del prodotto). Il compenso per il rischio è il profitto.

L'economista definisce produzione qualsiasi modificazione o trasformazione che aumenti la utilità di ciò che è a disposizione dei soggetti.

Si distinguono vari tipi di trasformazione:

● Trasformazione materiale

Ad es. un lingotto di metallo viene fuso per creare un gioiello; lamiere e altri componenti vengono prodotti e assemblati per ottenere un'automobile

● Trasformazione nel tempo

Tutte le operazioni di magazzinaggio, conservazione in celle frigorifere, inscatolamento, essiccazione, salatura, liofilizzazione, permettono ad un prodotto deperibile di essere consumato in un momento successivo (formaggi, insaccati, frutta secca ecc.)

● Trasformazione nello spazio

Tutte le operazioni di trasporto modificano la posizione dei beni nello spazio

● Trasformazione nel modo

Tutte le operazioni svolte dai commercianti che acquistano merce sfusa dal grossista, la mettono a disposizione in piccole porzioni o in esemplari singoli vicino alla abitazione dei clienti, offrono servizi di consulenza, possono essere considerate "trasformazioni nel modo"

L’imprenditore ha di fronte delle scelte:

▸ Quali tecnologie produttive adottare

▸ Quali prodotti offrire

▸ Quale quantità di prodotto immettere nel mercato (prezzo-quantità)

Il fine dell’imprenditore è massimizzare i profitti

Osserviamo la figura 0603060951, con lo schema dei rapporti tra famiglie e imprese in un sistema economico semplificato:

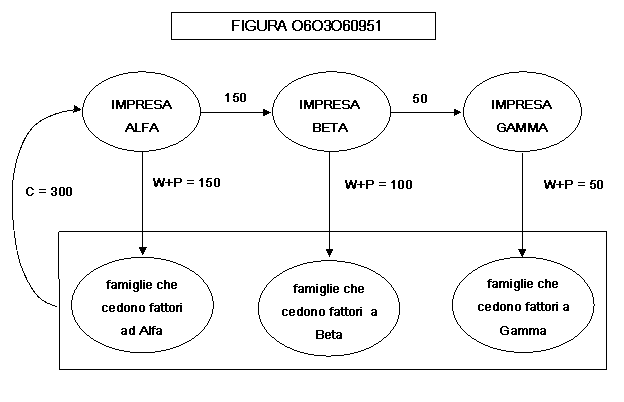
L’impresa Alfa produce automobili, utilizzando lamiere che paga lire 150 all’impresa Beta.

L’impresa Beta produce lamiere, utilizzando minerale che paga lire 50 all’impresa Gamma

L’impresa Gamma produce minerale senza utilizzare beni strumentali acquistati da altre imprese

I beni finali prodotti dal sistema economico consistono in auto per un valore di 300 lire, che costituiscono l’incasso dell’impresa Alfa (freccia verticale dalle famiglie all’impresa Alfa)

Ciascuna impresa, una volta pagato il valore dei beni intermedi utilizzati, distribuisce tutto il rimanente alle famiglie che hanno preso parte alla produzione, sotto forma di flusso W+P di

● salari

● profitti

● stipendi

● interessi

● royalties (compensi per i brevetti utilizzati)

● rendite (compenso ai proprietari dei terreni, delle miniere e delle altre risorse naturali utilizzate)

Tra le famiglie che hanno preso parte alla produzione includiamo ovviamente anche quelle degli imprenditori.

Possiamo subito vedere che i flussi W+P dalle imprese alle famiglie sono pari a 150+100+50 = 300, e cioè hanno lo stesso valore del prodotto finale, costituito da automobili (300).

Ma in questo grafico è anche vero che la produzione eguaglia la domanda aggregata (in questo caso la sola domanda delle famiglie).

Per “valore aggiunto” di una impresa si intende la differenza tra il ricavo o il costo dei beni strumentali non durevoli impiegati. Tutto il valore aggiunto di una impresa va alle famiglie. Il valore aggiunto di ciascuna impresa è quindi pari al flusso verticale posto sotto di essa.

Come si vede, in una economia chiusa, tre sono i concetti equivalenti che danno lo stesso valore:

▸ Valore dei beni finali prodotti

▸ Somma dei valori aggiunti

▸ Domanda aggregata

In sintesi, tutto il valore dei beni finali prodotti dalle imprese nell’unità di tempo (mese, anno, etc.) viene distribuito alle famiglie sotto forma di flusso W+P di salari, stipendi, profitto, royalties, rendite.

Le grandezze della teoria della produzione

back to index

PT_L(5) “Prodotto totale ottenuto con 5 unità di fattore lavoro, tenendo fisso il fattore capitale”

Il fattore lavoro è variabile e può assumere i valori 1, 2, 3, … ecc., mentre il fattore capitale è fisso (es. K = 7).

PT_K(5) “Prodotto totale ottenuto con 5 unità di fattore capitale, tenendo fisso il fattore lavoro”

Il fattore capitale è variabile e può assumere i valori 1, 2, 3, … ecc., mentre il fattore lavoro è fisso (es. L = 7).

PMA_L(5) “Prodotto marginale ottenuto con l’ultima di 5 unità di fattore lavoro impiegato, tenendo fisso il fattore capitale”

PMA_K(5) “Prodotto marginale ottenuto con l’ultima di 5 unità di fattore capitale impiegato, tenendo fisso il fattore lavoro”

PMAP_L(5) “Prodottività marginale ponderata della 5^ unità di fattore lavoro impiegato, tenendo fisso il fattore capitale”

PMAP_K(5) “Prodottività marginale ponderata della 5^ unità di fattore capitale impiegato, tenendo fisso il fattore lavoro”

PME_L(5) “Prodotto medio ottenuto con 5 unità di fattore lavoro impiegato, tenendo fisso il fattore capitale”

PME_K(5) “Prodotto medio di 5 unità di fattore capitale impiegato, tenendo fisso il fattore lavoro”

K Quantità di fattore capitale impiegato

L Quantità di fattore lavoro impiegato

CT(5) “Costo totale di 5 unità di prodotto”

Costo totale sostenuto per produrre n unità di prodotto

= CME(5) ⋅ 5

CMA(5) “Costo marginale della 5^ unità di prodotto”

= CT(5) – CT(4)

CME(5) “Costo medio di 5 unità di prodotto”

CTF(5) “Costo totale fisso di 5 unità di prodotto”

Costo dei fattori fissi impiegati per produrre 5 unità di prodotto

CTV(5) “Costo totale variabile di 5 unità di prodotto”

Costo dei fattori variabili impiegati per produrre 5 unità di prodotto

CMEF(5) “Costo medio fisso di 5 unità di prodotto”

CMEV(5) “Costo medio variabile di 5 unità di prodotto”

CTL(5) “Costo totale di lungo periodo di 5 unità di prodotto”

CTFL(5) “Costo totale fisso di lungo periodo di 5 unità di prodotto”

CTVL(5) “Costo totale variabile di lungo periodo di 5 unità di prodotto”

CMEL(5) “Costo medio di lungo periodo di 5 unità di prodotto”

CMEFL(5) “Costo medio fisso di lungo periodo di 5 unità di prodotto”

CMEVL(5) “Costo medio variabile di lungo periodo di 5 unità di prodotto”

RT(5) “Ricavi totali di 5 unità di prodotto”

Ricavi totali ottenuti dalla vendita di 5 unità di prodotto

= RME(5) ⋅ prezzo di vendita di 5 unità

RME(5) “Ricavo medio di 5 unità di prodotto”

RMA(5) “Ricavo marginale della 5^ unità di prodotto”

= RT(5) – RT(4)

PRT(5) “Profitto totale di 5 unità di prodotto”

Profitto ottenuto dalla vendita di 5 unità di prodotto

= RT(5) – CT(5)

= PRME(5) ⋅ 5

PRMA(5) “Profitto marginale della 5^ unità di prodotto

Aumento dei profitti totali ottenuto a seguito della vendita della 5^ unità di prodotto

= PRT(5) – PRT(4)

= RMA(5) – CMA(5)

PRME(5) “Profitto medio di 5 unità di prodotto

La funzione di produzione

back to index

La tecnologia è l’insieme di tutti i processi produttivi disponibili per produrre un certo prodotto PT (output) a partire da una data quantità di fattori

Una tecnologia è rappresentata da una funzione di produzione.

La funzione di produzione è la relazione che collega un gruppo di grandezze che rappresentano la quantità di fattori impiegati alla grandezza che rappresenta il prodotto che con esse si ottiene.

Dati n fattori la funzione di produzione viene presentata nei testi di economia con il simbolismo:

PT = f(F₁, F₂, …, F_n)

dove F₁,…, F_n sono i fattori impiegati (input) e PT è la quantità di prodotto ottenuta (output).

Malgrado i fattori di produzione siano numerosi gli economisti, per semplicità, li raggruppano in tre categorie:

▸ Natura

▸ Beni strumentali

▸ Lavoro

Mettendo insieme natura e beni strumentali sotto la dicitura “K” (capitale fisico) e aggiungendo “L” (lavoro) essi studiano una funzione di produzione semplificata, con soli due fattori, capitale K e lavoro L:

PT = f(K,L)

In questa espressione PT si definisce “output” e la combinazione di K ed L utilizzata per produrlo si definisce “input”.

La funzione può assumere la forma di una formula matematica del più vario tipo:

PT = K + L

PT = 3K + 2L

PT = 2K² + 2L³

Una funzione di produzione molto conosciuta è la funzione di Cobb-Douglas:

PT = a ⋅ L^b ⋅ K^c b + c = 1

Una funzione di produzione può essere visualizzata in un grafico come quello sottostante.

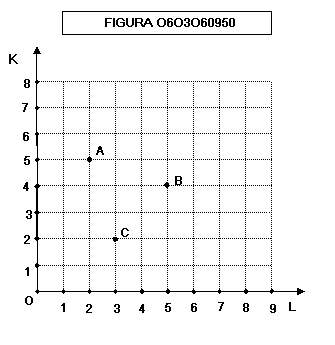
In tale grafico il fattore lavoro può essere indifferentemente misurato in numero di lavoratori occupati o in ore-lavoro.

In tale grafico, ogni punto rappresenta una combinazione di capitale K e di lavoro L:

A = 5 unità di capitale + 2 unità di lavoro

B = 4 unità di capitale + 5 unità di lavoro

C = 2 unità di capitale + 3 unità di lavoro

Data una funzione di produzione a coefficienti flessibili, ad ogni punto è associato una determinato output, cioè il prodotto ottenuto dalla combinazione di fattori rappresentata dal punto.

Consideriamo ad un esempio la funzione di produzione:

PT = 3K + 2L

avremo allora:

A ➙ PT = 3 ⋅ 5 + 2 ⋅ 2 = 19

B ➙ PT = 3 ⋅ 4 + 2 ⋅ 5 = 22

C ➙ PT = 3 ⋅ 2 + 2 ⋅ 3 = 12

e potremo visualizzare questi valori sul grafico 0603060952:

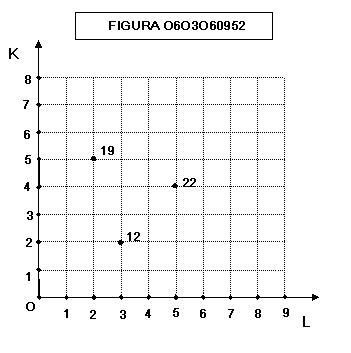
oppure (solo per alcune coppie di valori che scegliamo) in una tabella:

TAB. 0603022051
K	L	PT
1	2	7
1	3	9
2	2	10
2	3	12
3	4	17
3	5	19
4	5	22
5	6	27
6	7	32
8	10	44

La visualizzazione tramite tabella o grafico è necessaria quando la relazione tra input e output è ottenuta da misurazioni empiriche e non si riesce a trovare una formula matematica che le esprima con precisione.

La funzione di produzione indica, per ciascuna combinazione di capitale e lavoro, l’output ottenibile con la tecnica più efficiente disponibile nel momento considerato. Le tecniche meno efficienti non sono quindi considerate.

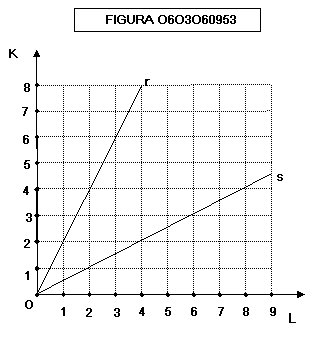
Nel grafico della funzione di produzione (figura 0603060953) una retta che passa per l’origine individua tutte le combinazioni che hanno in comune la stessa proporzione tra capitale e lavoro. Ad es. la retta r individua tutte le combinazioni in cui la quantità di capitale è doppia di quella di lavoro (cosiddetti metodi di produzione “capital-intensive”, tipici dei paesi industrializzati), mentre la retta s individua tutte le combinazioni in cui la quantità di lavoro è doppia di quella di capitale (cosiddetti metodi di produzione “labour-intensive”, tipici dei paesi sottosviluppati). Rapporti differenti (linee differenti) individuano differenti processi o metodi di produzione. Un processo o metodo di produzione consiste in un dato rapporto in cui vengono combinati i fattori.

Non necessariamente la tecnologia consente di produrre con qualsiasi combinazione di fattori (ad es. è impossibile produrre scarpe con solo lavoro e zero beni strumentali come cuoio). Esistono funzioni di produzione dette “a coefficienti fissi”, che non permettono di ottenere un output per qualsiasi combinazione produttiva (es. è possibile produrre una scarpa con 1 kg di cuoio e 1 ora di lavoro ma non con 1 grammo di cuoio e 10 ore di lavoro). Tra di esse vi sono quelle che consentono di adottare solo un numero finito di processi produttivi: ad esempio, nel grafico di figura 0603060954, le uniche combinazioni attuabili sono quelle lungo le rette r,s,t,u, cioè rispettivamente il metodo di produzione che utilizza due unità di capitale per una unità di lavoro, il metodo che utilizza due unità di lavoro per ogni unità di capitale, il metodo che utilizza una unità di lavoro per ogni unità di capitale e il metodo che utilizza tre unità di capitale per ogni unità di lavoro.

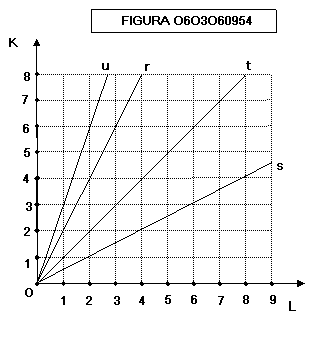
Nei testi di economia vengono prevalentemente studiate funzioni a coefficienti flessibili: anche noi supporremo che ogni punto del grafico rappresenti una combinazione attuabile, che fornisce un determinato output.

Funzioni di produzione omogenee

back to index

Quando si verifica la condizione:

f(n ⋅ K , n ⋅ K) = n^α ⋅ f(K , L)

si ha una funzione omogenea di grado α (con α che può assumere i valori 1, 2, …)

Una funzione omogenea di grado 1 sarà pertanto una funzione del tipo:

f(n ⋅ K , n ⋅ K) = n¹ ⋅ f(K , L) = n ⋅ f(K , L)

Con una tale funzione, se raddoppiamo, triplichiamo ecc. la quantità di tutti i fattori, la quantità di prodotto raddoppia triplica ecc.

Le funzioni omogenee non sono le sole che possono presentare un tale fenomeno: ma le funzioni non omogenee lo presentano solo per determinate combinazioni di fattori e non per altre, oppure possono mostrare una variazione della proporzionalità in relazione ai livelli di produzione.

Le economie esterne

back to index

● Esternalità positive:

guadagni che una attività produttiva o di consumo fa realizzare ad un altro produttore o consumatore, ma che non si riesce a farsi pagare.

Chiameremo le esternalità positive realizzate dal produttore economie esterne di produzione e le esternalità positive realizzate dal consumatore economie esterne di consumo.

Esempio: le coltivazioni di alberi da frutta di un agricoltore favoriscono la produzione di miele di un altro agricoltore

Esempio: il fatto che una bella ragazza frequenti una palestra o uno stabilimento balneare giova agli affari dell'impresa che gestisce la palestra o lo stabilimento balneare

Esempio: Il fatto che lo stato fornisca cure mediche e istruzione alla popolazione favorisce le imprese, che hanno lavoratori più istruiti e meno assenze per malattia

● Esternalità negative:

Danni economici che una attività produttiva o di consumo provoca ad un'altro produttore o consumatore, ma che non si è tenuti a pagare.

Chiameremo le esternalità negative realizzate dal produttore diseconomie esterne di produzione e le esternalità positive realizzate dal consumatore diseconomie esterne di consumo.

Esempio: Una discoteca provoca rumori e schiamazzi notturni che disturbano gl occupanti di un appartamento e ne riducono persino il valore

Esempio: Una impresa che immette fumi nell'atmosfera costringe le famiglie a lavare più frequentemente tende e abiti, e quindi ad una maggiore spesa per detersivi

Le economie interne (tra cui i rendimenti di scala)

back to index

Nel lungo periodo l’impresa può variare la quantità di tutti i fattori impiegati.

Se i costi medi di una impresa diminuiscono all’aumentare della quantità prodotta si dice che essa va incontro ad economie di scala.

Viceversa, se i costi medi di una impresa aumentano all’aumentare della quantità prodotta, si dice che essa va incontro a diseconomie di scala.

Gli economisti distinguono le economie esterne e diseconomie esterne, da un lato, influenzate da fattori per cui l’impresa paga un costo ed economie interne e diseconomie interne, influenzate da fattori per cui l’impresa non paga un costo o non riceve un risarcimento. Di queste ultime parleremo più avanti.

Tra le economie interne gli studiosi hanno preso in esame i rendimenti di scala, cioè i casi in cui l’impresa aumenta tutti i fattori della stessa proporzione (es. ne raddoppia, triplica, ecc. la quantità), ottenendo una variazione della produzione che può essere proporzionale, più che proporzionale o meno che proporzionale.

Mentre i rendimenti di scala sono un caso di economie di scala dovute a fattori tecnici, esistono economie di scala dovute a fattori non tecnici (es. monetari).

In sintesi, abbiamo il seguente prospetto, che ci aiuta ad inquadrare i rendimenti di scala all’interno della categoria delle economie di produzione:

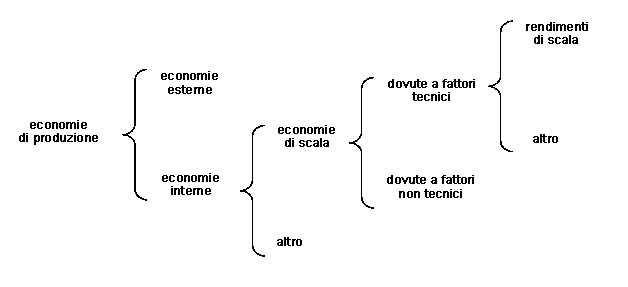
Come si è già detto, il fenomeno dei rendimenti di scala si presenta nel lungo periodo quando i fattori vengono variati tutti nella stessa proporzione. Esso si presenta quando l’impresa si muove lungo una linea che passa per l’origine, come quelle già mostrate in fig. 0603060953

Si hanno rendimenti di scala crescenti se la produzione cresce più che proporzionalmente al crescere dei fattori.

Si hanno rendimenti di scala costanti se la produzione cresce proporzionalmente al crescere dei fattori

Si hanno rendimenti di scala decrescenti se la produzione cresce meno che proporzionalmente al crescere dei fattori.

Ad esempio si può verificare che una funzione del tipo:

PT = 2L + K

ha rendimenti di scala costanti

Una funzione di produzione omogenea di grado α presenta rendimenti decrescenti di scala se α < 1, rendimenti crescenti di scala se α > 1 e rendimenti costanti di scala se α = 1

La esistenza di rendimenti crescenti di scala è dovuta a indivisibilità tecniche e/o manageriali. Generalmente, mentre è possibile raddoppiare la scala per la maggior parte dei processi, può non essere possibile dimezzarla.

Consideriamo ad esempio la tabella 0603052031 che mostra tre processi:

TABELLA 0603052031
Processo	Scala	Lavoro	Capitale	Output (PT)
A	piccola	1	1	1
B	media	50	50	100
C	grande	100	100	400

In tutti e tre i processi la proporzione dei fattori è 1 : 1, ma i rendimenti sono crescenti: passando dal processo A al processo B i fattori vengono moltiplicati per 50 mentre il prodotto risulta moltiplicato per 100; passando dal prodotto B al prodotto C i fattori vengono raddoppiati, mentre il prodotto quadruplica.

Se supponiamo – come accade nella realtà – che il processo di scala media non può essere utilizzato per produrre meno di 100 unità e il processo di grande scala non può essere utilizzato per produrre meno di 400 unità una impresa che sta crescendo non potrà utilizzare il processo B fino a che non sarà arrivata a produrre 100 unità e non potrà utilizzare il processo C fino a che non sarà arrivata a produrre 400 unità.

Una delle ragioni per cui i processi di grande scala risultano più efficienti risiede nella specializzazione del lavoro che essi consentono di attuare.

In una piccola macelleria, una sola persona, per macellare un bovino, deve compiere 100 distinte operazioni, cambiando di volta in volta strumenti.

In una grande macelleria, che macella 100 bovini anziché un bovino al giorno, possono essere impiegate 100 persone, ciascuna delle quali potrà specializzarsi in una sola operazione, che essa compirà più velocemente rispetto al lavoratore della piccola macelleria.

La specializzazione del lavoro è tipica delle società moderne e industrializzate ed è andata aumentando a partire dal medioevo.

La specializzazione del lavoro comporta a sua volta un incremento degli scambi nel sistema: ciascun membro del sistema economico si specializza in una sola attività e deve ricevere dagli altri tutto ciò che egli non produce.

Un’altra importante causa di aumento di produttività del lavoro è la meccanizzazione o automazione. Più grande è la scala del processo produttivo, più conveniente è introdurre l’uso di macchine, che sono normalmente costose e vanno ammortizzate su grandi volumi di produzione. Un esempio tipico è l’industria automobilistica, dove il crescere delle dimensioni delle cause produttrici ha permesso l’introduzione della catena di montaggio.

Graficamente, se la funzione di produzione è omogenea e a rendimenti costanti di scala essa si presenta come nel grafico di figura 0603031651:

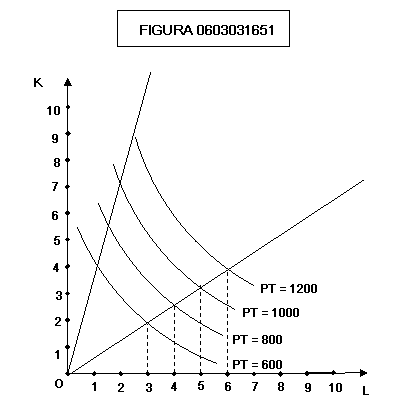
Se la funzione di produzione è omogenea e a rendimenti crescenti di scala essa si presenta come nel grafico di figura 0603031653:

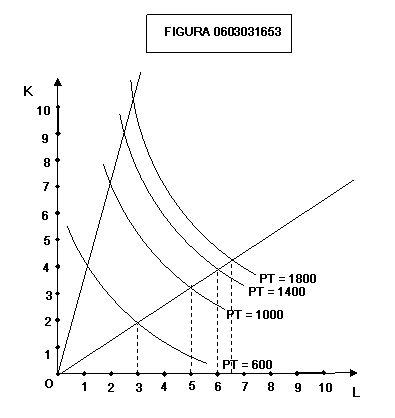
Se la funzione di produzione è omogenea e a rendimenti crescenti di scala essa si presenta come nel grafico di figura 0603031655:

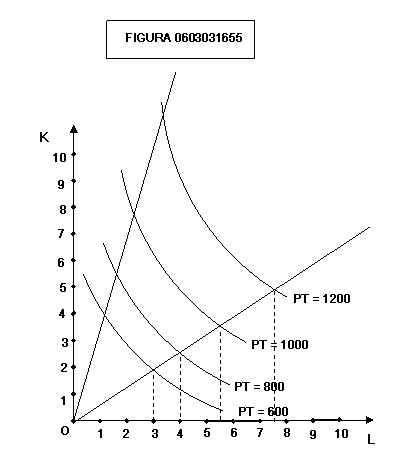
Il caso più frequente dovrebbe essere quella dei rendimenti costanti: se tutti i fattori vengono applicati in quantità crescenti, ma sempre nella medesima proporzione, non vi è alcuna ragione per attendersi che il prodotto cresca in misura diversa.

Le ragioni per cui una impresa va incontro a rendimenti crescenti o decrescenti di scala saranno esaminate più avanti, quando si parlerà dei costi di lungo periodo.

L’isoquanto

back to index

Un isoquanto è l’insieme dei punti che rappresentano combinazioni che forniscono lo stesso prodotto totale (figura 0603061000):

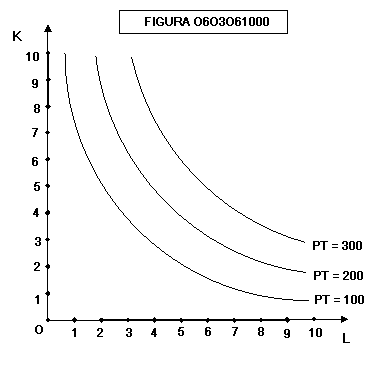
Gli isoquanti sono tracciati tenendo conto della funzione di produzione della impresa. Quando la funzione di produzione dell’impresa cambia gli isoquanti si spostano

Ad esempio, se il progresso tecnico consente di mettere a punto tecniche di produzione più efficienti, uno stesso isoquanto si sposta verso l’origine (figura 0603061001):

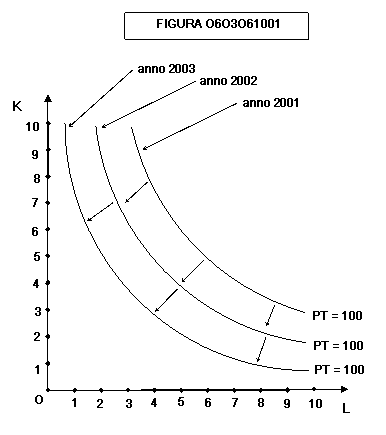
La forma normale dell’isoquanto è convessa verso l’origine a causa della legge del rendimento decrescente del fattore variabile (figura 0603061002):

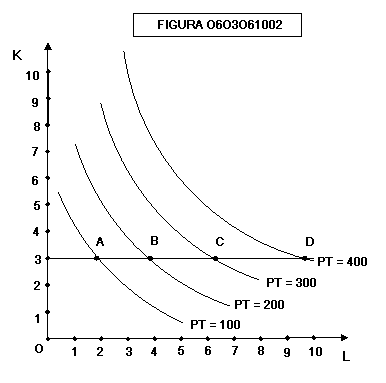
Come vedremo, se un fattore viene lasciato fisso (es. K = 3 nel grafico) e viene costantemente aumentato il fattore variabile (es. ad un terreno agricolo di estensione fissa vengono aggiunti sempre più fertilizzante e manodopera) arriverà il momento che quantità successive di fattore variabile produrranno incrementi sempre minori della produzione. Questo è proprio ciò che si vede dal grafico: i segmenti AB, BC, CD sono via via più lunghi e questo vuol dire che, per passare da 100 a 200 a 300 a 400 unità prodotto necessita una quantità sempre maggiore di fattore variabile (lavoro).

Eccezionalmente gli isoquanti potrebbero avere anche altre forme (figure 0603061003 e fig. 0603061004):

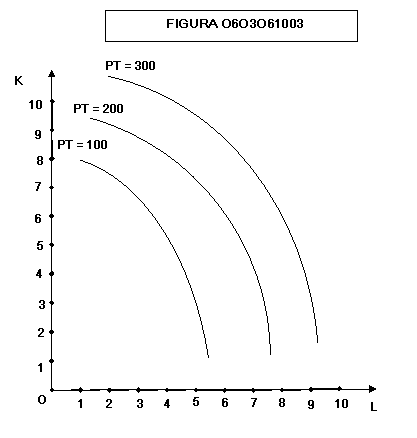
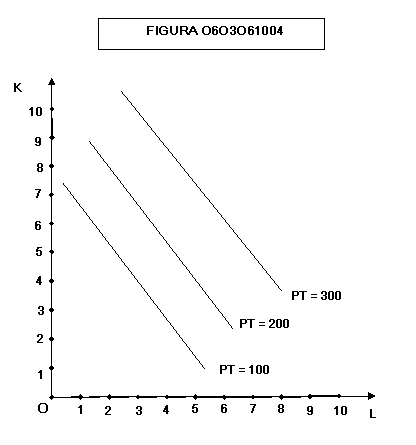
ma gli economisti si occupano prevalentemente di quelli indicati nel primo grafico.

Per “processo produttivo” o “metodo produttivo” intendiamo un processo che combina i fattori in una data proporzione.

A diverse proporzioni nella combinazione dei fattori corrispondono, secondo l’economista, diversi metodi produttivi (fig. 0603061005):

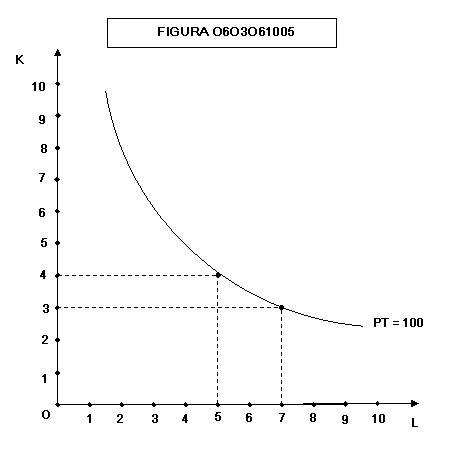
Come vediamo dalla figura 0603061005, la stessa quantità di prodotto può essere ottenuta utilizzando 4 unità di capitale e 5 unità di lavoro oppure 3 unità di capitale e 7 unità di lavoro. Si tratta di due diversi metodi o processi produttivi.

Nella figura 0603031615 le linee che partono dall’origine corrispondono a diversi processi produttivi: i punti di ogni linea rappresentano combinazioni in cui capitale e lavoro sono combinati sempre nella stessa proporzione. Ad esempio la linea r è quella delle combinazioni in cui la quantità di lavoro è doppia di quella di capitale, mentre la linea s è quella delle combinazioni in cui la quantità di capitale è doppia di quella del lavoro.

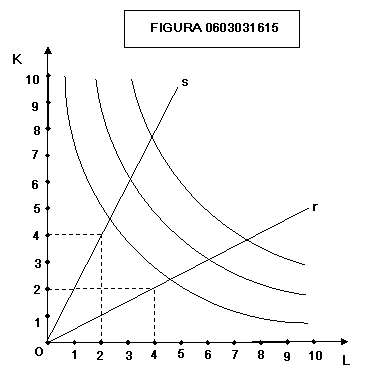
Esistono infinite linee che attraversano uno stesso isoquanto, e questo significa che una stessa quantità di prodotto può essere ottenuta con una varietà infinita di tecniche produttive.

Un metodo di produzione A è tecnicamente efficiente rispetto ad un altro metodo B se A usa meno di almeno un fattore e non di più degli altri fattori rispetto al metodo B. Per esempio, dei due metodi:

A : 2L + 3K = 1 unità di prodotto

B : 3L + 3K = 1 unità di prodotto

il metodo B è chiaramente il meno efficiente.

Ci sono invece dei metodi non confrontabili:

C : 2L + 3K = 1 unità di prodotto

D : 3L + 2K = 1 unità di prodotto

In questo caso non possiamo concludere né che C sia più efficiente di D né il contrario. Entrambi i metodi vanno perciò considerati efficienti.

La forma completa dell’isoquanto è mostrata nella figura 0603061006. Oltre le linee tratteggiate si può vedere che i processi produttivi diventano inefficienti perché impiegano, rispetto alle combinazioni indicate dai punti, più capitale e più lavoro per produrre la stessa quantità di prodotto. Noi limiteremo pertanto lo studio degli isoquanti alla parte contenuta tra le linee tratteggiate.

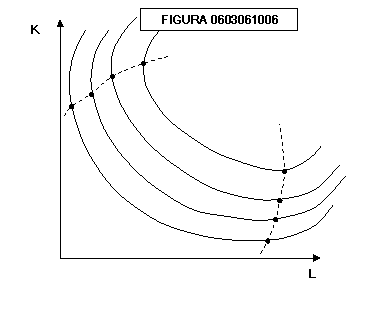
La pendenza dell’isoquanto

back to index

La pendenza finita dell’isoquanto relativa all’arco AB viene chiamata “saggio marginale di sostituzione” e indica la quantità di capitale necessaria per sostituire una unità di lavoro:

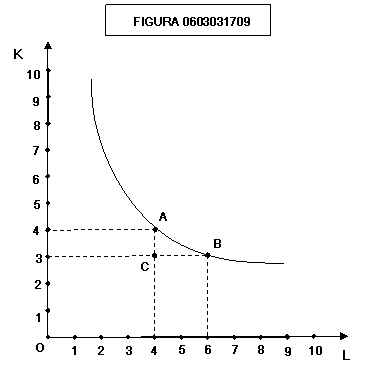
Nel grafico di figura 0603031709 si vede come, per spostarsi da A a B o da B ad A occorre sostituire due unità di lavoro con una unità di capitale o viceversa.

Si definisce “saggio marginale di sostituzione tecnica del fattore lavoro al fattore capitale” (più brevemente, “saggio marginale di sostituzione di L a K”) è il rapporto tra una quantità di fattore capitale e della quantità di fattore lavoro che è in grado di sostituirla fornendo lo stesso output. Nella figura essa è data dal rapporto CA/CB

Il saggio marginale di sostituzione tecnica del lavoro al capitale SMS_L,K sarà pertanto:

Il saggio marginale di sostituzione del lavoro al capitale equivale al rapporto tra l’incremento di prodotto ottenuto con la quantità di lavoro CB e l’incremento di prodotto ottenuto con la quantità di capitale CA:

L’isocosto

back to index

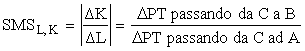
Un isocosto è l’insieme dei punti che rappresentano combinazioni capitale-lavoro che hanno per l’imprenditore lo stesso costo totale (CT) (fig. 0603061007):

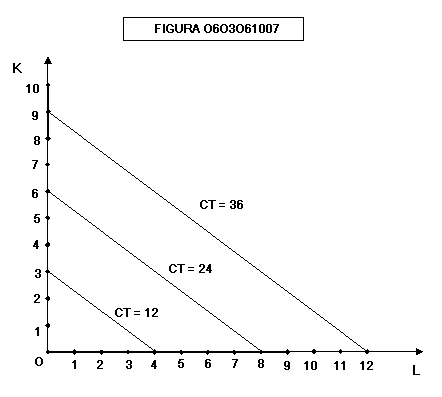
Gli isocosti sono tracciati supponendo che una unità di fattore capitale costi 4 € e che una unità di fattore lavoro costi 3 €

Come si puo vedere, se consideriamo un costo maggiore, l’isocosto si sposta verso destra parallelamente a se stesso.

Effetto sull’isocosto di un cambiamento dei prezzi dei fattori

back to index

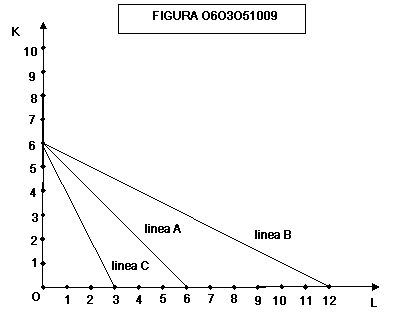
Nella figura 0603051009 la linea A è stata tracciata supponendo che l’imprenditore disponga di una somma di 12 €, che una unità di capitale abbia un prezzo di 2 € e che una una unità di lavoro abbia un prezzo di 2 €.

La linea B è stata tracciata supponendo che il prezzo del lavoro si dimezzi a 1 €

La linea C è stata tracciata supponendo che il prezzo del lavoro raddoppi a 4 €

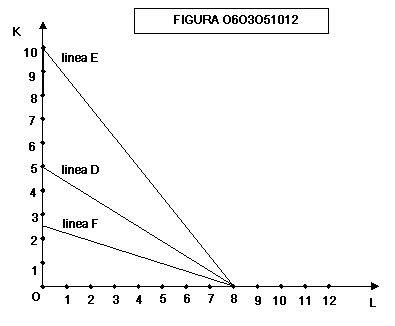
Nella figura 0603051012 la linea D è stata tracciata supponendo che l’imprenditore disponga di una somma di 40 €, che una unità di capitale abbia un prezzo di 8 € e che una una unità di lavoro abbia un prezzo di 5 €.

La linea E è stata tracciata supponendo che il prezzo del capitale si dimezzi a 4 €

La linea C è stata tracciata supponendo che il prezzo del lavoro raddoppi a 16 € (in questo caso l’imprenditore potrà acquistare solo 2,5 unità di fattore capitale).

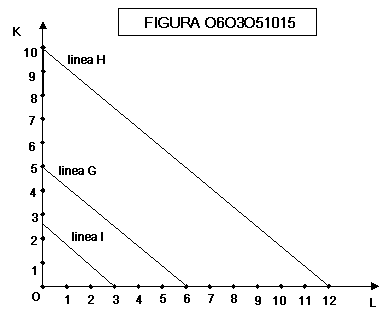
Nella figura 0603051015 la linea G è stata tracciata supponendo che l’imprenditore disponga di una somma di 30 €, che una unità di capitale costi 6 € e che una unità di lavoro costi 5 €

Se il prezzo del capitale e del lavoro raddoppiano si passa dalla linea G alla linea I

Se il prezzo del capitale e del lavoro dimezzano si passa dalla linea G alla linea H

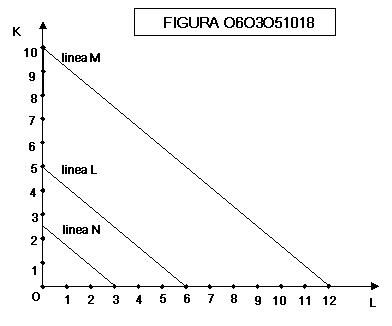
Nella figura 0603051018 la linea L è stata tracciata supponendo che l’imprenditore disponga di una somma di 30 €, che una unità di capitale costi 6 € e che una unità di lavoro costi 5 €

Se la somma a disposizione dell’imprenditore raddoppia (60 €) si passa dalla linea L alla linea M

Se la somma a disposizione dell’imprenditore dimezza (15 €) si passa dalla linea L alla linea N

La pendenza dell’isocosto

back to index

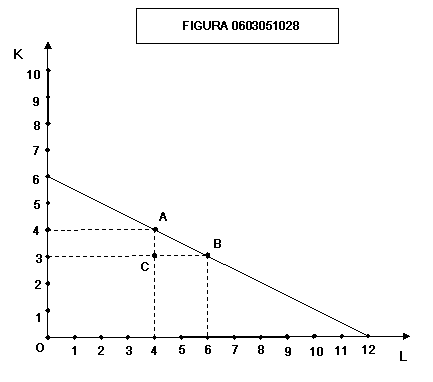
Nella figura 0603051028 l’isocosto è stato tracciato supponendo che l’impresa disponga di 24 €, che il prezzo di una unità di capitale sia di 4 € e che il prezzo di una unità di lavoro sia di 2 €.

La pendenza dell’isocosto è data dal rapporto

Il valore assoluto di questo rapporto equivale a quello tra il costo di una unità di lavoro e quello di una unità di capitale:

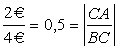
L’equilibrio dell’imprenditore determinato mediante isoquanto e isocosto

back to index

Con l’isocosto e l’isoquanto viene studiato il comportamento dell’impresa che ha un obiettivo che può essere formulato in due modi:

▸ Dato un budget fisso (cioè data una certa somma) massimizzare il prodotto (cioè ottenere il prodotto maggiore possibile)

▸ Dato un prodotto che si vuole ottenere, minimizzare i costi (cioè sostenere i costi più bassi possibili)

In entrambi i casi si parla di “combinazione ottima dei fattori” per indicare la combinazione capitale-lavoro che permette di raggiungere uno dei due obiettivi.

Noi ci riferiremo al problema nella prima forma: dato un isocosto, determinare il punto di massima produzione

Supponendo quindi che nella figura 0603051049 l’imprenditore disponga di una somma tale per cui il suo isocosto è quello mostrato, egli dovrà scegliere il punto dell’isocosto che gli fornisce il massimo prodotto totale.

Egli scarterà il punto D, che gli fornisce solo 100 unità di prodotto.

Scarterà anche i punti B e C perché gli forniscono solo 200 unità di prodotto

Scarterà anche il punto E, perché non è raggiungibile con la somma di cui dispone.

Il punto scelto sarà pertanto il punto A, in cui l’isocosto ha tangenza con uno degli isoquanti.

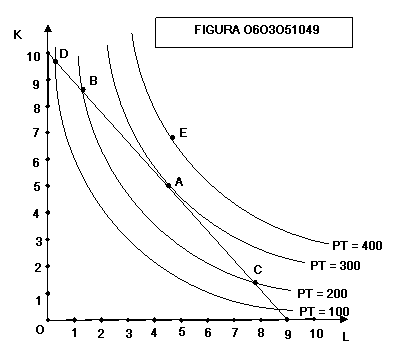
Ricordiamo che questa è una analisi di lungo periodo, perché nel caso del breve periodo la figura 0603051459 mostra come, dato un isoquanto, l’imprenditore, che utilizza 3 unità di fattore fisso, ha la sola scelta, per produrre il massimo possibile, di impiegare 6 unità di fattore variabile.

Nella figura 0603051503 possiamo vedere l’effetto, sulla scelta dell’imprenditore, di un aumento del prezzo del fattore lavoro:

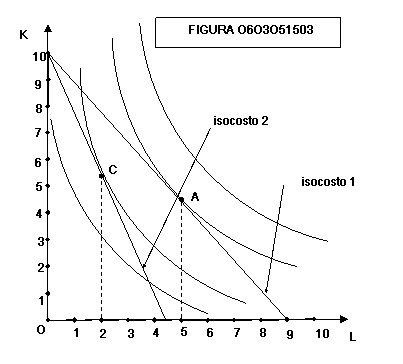
Mentre l’isocosto prima della variazione di prezzo (isocosto 1) individuava il punto di equilibrio A, il nuovo isocosto (isocosto 2) è ruotato verso l’origine ed è ora tangente al punto C, che è il nuovo punto di equilibrio. A seguito di un aumento di prezzo l’impresa ha ridotto l’impiego del fattore lavoro da 5 unità a 2 unità.

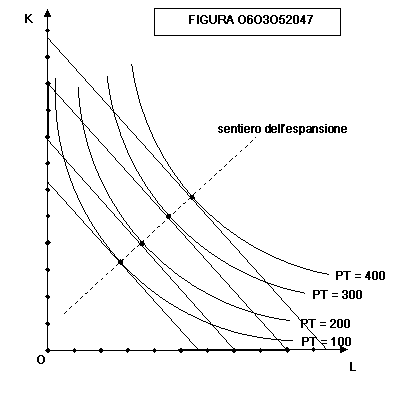
La linea che, nel lungo periodo, unisce tutti i punti si equilibrio toccati da una impresa che aumenta la produzione prende il nome di “sentiero dell’espansione (dell’output)”. Si tenga presente che questa linea non è necessariamente retta.

La legge della eguaglianza delle produttività marginali ponderate

back to index

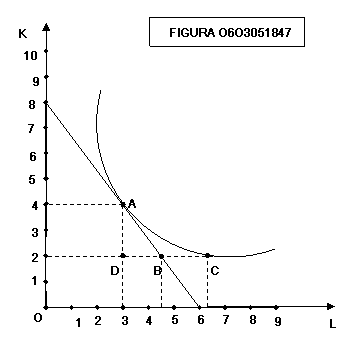
Come si può vedere dalla figura 0603051847 la pendenza dell’isoquanto e la pendenza dell’isocosto differiscono.

La pendenza dell’isocosto è pari a

La pendenza dell’isoquanto è pari a

Abbiamo già notato come il valore assoluto del rapporto è pari al rapporto tra la quantità di prodotto ottenuta passando dal punto D al punto C e la quantità di prodotto ottenuta passando dal punto D al punto A:

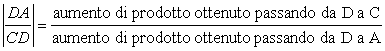
Ma l’aumento di prodotto ottenuto passando da D a C è la produttività marginale del lavoro PMA_L, mentre l’aumento di prodotto ottenuto passando da D ad A non è altro che la produttività marginale del capitale PMA_K. Possiamo così scrivere:

e cioè:

Se consideriamo archi più piccoli di AC per calcolare la pendenza finita, il punto C si avvicina al punto B. Considerando archi sempre più piccoli, BD e CD tenderanno quindi a coincidere. Per archi infinitamente piccoli sull’isoquanto la differenza tra la lunghezza di BD e di CD sarà trascurabile, e potremo quindi scrivere:

Dalla eguaglianza così ottenuta:

si ricava:

e cioè:

PMAP_L = PMAP_K

Questa è la condizione di equilibrio dell’imprenditore, ed è nota come legge dell’eguaglianza delle produttività marginali ponderate.

Brevissimo, breve, lungo, lunghissimo periodo

back to index

● Il periodo brevissimo (o “periodo di cassa” o “periodo di magazzino”) non consente all’impresa di variare alcun fattore

Perciò se aumenta la domanda dei consumatori l’impresa non è in grado di aumentare la produzione e l’unica cosa che può fare è alzare i prezzi

● Nel periodo breve non tutti i fattori possono essere variati: almeno un fattore è fisso e non aumentabile. Gli altri prendono il nome di “fattori variabili”.

Un tipico fattore fisso nel breve peruiodo sono gli impianti (capitale). Una volta installati gli impianti (capannoni, macchinari ecc.) l’imprenditore può solo decidere quanti lavoratori impiegare, perché la dotazione di capitali nel breve periodo è fissa.

● Nel periodo lungo tutti i fattori possono variare, ma non la tecnologia

Nel periodo lungo anche i fattori naturali possono essere aumentati tramite nuove invenzioni (dal legno al carbone, dal carbone al petrolio, dal petrolio all’energia atomica, dall’energia atomica all’energia di fusione e all’energia solare ecc.)

● Nel periodo lunghissimo varia anche la tecnologia

Non esiste una misura precisa di tali periodi: in un settore industriale il periodo breve potrebbe essere addirittura di anni (nel settore energetico la messa in funzione di una nuova diga o centrale richiede diversi anni) o di poche settimane (una panetteria può ordinare e farsi istallare un nuovo forno in alcune settimane).

I dati dell’impresa Alfa

back to index

● Funzione di produzione:

● Funzione di domanda:

Domanda = 100 – Prezzo ⋅ 10

(si tratta dell’equazione della curva di domanda dell’impresa mostrata in figura 0603080922)

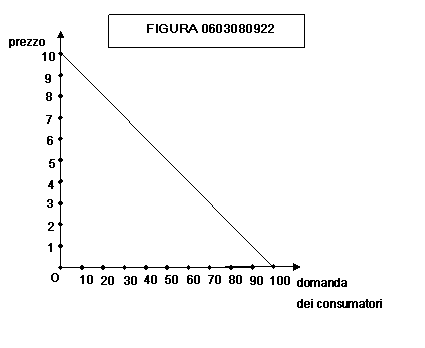
● Quantità di fattore fisso impiegata nel breve periodo: K = 5

● Costo di una unità di fattore lavoro: 4 €

● Costo di una unità di fattore capitale: 8 €

Calcoliamo l’isoquanto dell’impresa Alfa

back to index

Il grafico dell’isoquanto può essere calcolato a partire dalla formula della funzione di produzione:

da cui:

Se in questa formula diamo a PT un valore costante (es. PT = 100) otteniamo l’isoquanto dei punti che forniscono PT = 100:

In questa formula K è la variabile dipendente (asse verticale) e L è la variabile indipendente (asse orizzontale).

Otteniamo così la tabella 0603061008:

TAB. 0603061008
L	K
1	33,3
2	23,6
3	19,3
4	16,7
5	14,9
6	13,7
7	12,6
8	11,8
9	11,1
10	10,5

Per capire il procedimento, calcoliamo ad esempio il valore di K relativo ad L = 5 ed ad un livello di produzione PT = 100

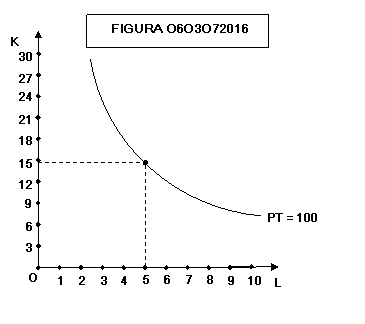
La formula da utilizzare è:

Troncando 14,94 alla prima cifra decimale si ottiene il valore 14,9 della tabella.

Calcoliamo, relativamente al breve periodo, il prodotto totale PT, il prodotto marginale PMA e il prodotto medio PME dell’impresa Alfa

back to index

Per “prodotto totale di n unità del fattore L” o “produttività totale di n unità del fattore L” PT_L(n) si intende, nel breve periodo, il prodotto ottenuto con n unità di L impiegando una quantità fissa di K. Essa si calcola a partire dalla funzione di produzione, sostituendovi i valori di K ed L (vedi esempio più avanti).

Il prodotto medio PME_L(n) si ottiene dividendo il prodotto totale PT_L(n) per n

Per “prodotto marginale di un fattore” o “produttività marginale di un fattore” si intende la variazione della produzione in corrispondenza di una variazione dell’impiego del fattore:

dove f è la funzione di produzione, K^̅ è un livello fisso di fattore capitale e ∆L è una variazione del fattore lavoro.

La nozione matematica di prodotto marginale considera variazioni ∆L molto piccole, vicine allo zero. Utilizzando un foglio elettronico normalmente, per ottenere la nozione matematica di prodotto marginale, si utilizzano variazioni dell’ordine di 0,00000000001.

La definizione matematica precisa è quella di “derivata parziale della funzione di produzione rispetto al lavoro”:

che si legge: “limite, per ∆L che tende a zero, del rapporto tra la variazione di f e della variazione di L”

Nei testi didattici di economia, invece, viene considerato ∆L = 1, in modo che la formula diventa:

Conformemente a questa formula, nei testi didattici il prodotto marginale di un dato fattore viene definito come “l’incremento che si ottiene nella produzione per effetto dell’aggiunta di una unità del fattore considerato” oppure come

“la variazione dell’output risultante da una variazione (molto piccola) del fattore stesso, mantenendo tutti gli altri fattori costanti”.

Noi utilizzeremo quest’ultima formula per calcolare il prodotto marginale

Consideriamo il breve periodo, in cui il fattore K è fisso (K = 5)

TABELLA 0603042018
K	L	PT_L(L)	PT_L(L–1)	PMA_L(L)	PME_L(L)
5	1	15,00	0,00	15,00	15,00
5	2	21,15	15,00	6,15	10,57
5	3	25,95	21,15	4,80	8,65
5	4	30,00	25,95	4,05	7,50
5	5	33,45	30,00	3,45	6,69
5	6	36,60	33,45	3,15	6,10
5	7	39,60	36,60	3,00	5,65
5	8	42,30	39,60	2,70	5,28
5	9	45,00	42,30	2,70	5,00
5	10	47,40	45,00	2,40	4,74

Calcoliamo ad esempio PT_L(5) tenendo fermo K = 5, tenendo presente che per ottenere la corrispondenza con la tabella vanno utilizzati valori di divisioni, moltiplicazioni o radici troncati a due cifre:

Per calcolare PMA_L(5) si può utilizzare la formula:

PMA_L(5) = PT_L(5) – PT_L(4) = 33,45 – 30 = 3,45

Per calcolare PME_L(5) utilizziamo la formula:

Nella tabella 0603072105 calcoliamo invece i valori relativi al capitale, e cioè PT_K, PMA_K, PME_K:

TABELLA 0603072107
K	L	PT_K(K)	PT_K(K–1)	PMA_K(K)	PME_K(K)
5	1	15,00	12,00	3,00	3,00
5	2	21,15	16,92	4,23	4,23
5	3	25,95	20,76	5,19	5,19
5	4	30,00	24,00	6,00	6,00
5	5	33,45	26,76	6,69	6,69
5	6	36,60	29,28	7,32	7,32
5	7	39,60	31,68	7,92	7,92
5	8	42,30	33,84	8,45	8,46
5	9	45,00	36,00	9,00	9,00
5	10	47,40	37,92	9,48	9,48

Calcoliamo ad esempio PT_K(5) tenendo fermo L = 4, tenendo presente che per ottenere la corrispondenza con la tabella vanno utilizzati valori di divisioni, moltiplicazioni o radici troncati a due cifre:

Per calcolare PMA_K(5) si può utilizzare la formula:

PMA_K(5) = PT_K(5) – PT_K(4) = 30 – 24 = 6

Per calcolare PME_K(5) utilizziamo la formula:

back to index

Nel breve periodo esistono fattori fissi che non possono variare, e fattori variabili. I costi dei fattori fissi prendono il nome di “costi fissi”.

Esempi di costi fissi sono:

▸ Le spese per il pagamento di interessi

▸ Le spese pubblicitarie

▸ Le spese di sorveglianza

▸ Le spese di pulizia dei locali

▸ Gli ammortamenti degli impianti, le spese per il deperimento e la riparazione degli edifici, le spese per la conservazione dei terreni ecc.

Per “ammortamento” di un determinato bene strumentale durevole gli economisti intendono le somme che rappresentano il logorio annuale di tale bene. In pratica, per poter rimpiazzare un bene strumentale acquistato, l’impresa deve accantonare, per ogni anno della sua vita utile, una somma di denaro che consenta, quando il bene non produrrà più, di acquistare un bene analogo. Queste somme annuali sono considerate il valore del logorio del bene strumentale, e chiamate ammortamenti. Esse sono costi fissi, che l’impresa paga sia che sfrutti l’impianto sia che non lo sfrutti.

Possiamo anche definire gli ammortamenti il costo annuale di un bene strumentale durevole: esso si ottiene all’incirca dividendo il costo del bene per il numero di anni durante i quali esso risulterà utile.

▸ Le spese di amministrazione generale (retribuzioni del personale di ufficio, degli addetti ai magazzini, del personale di sorveglianza ecc.)

▸ I costi di assicurazione ed i fitti, i canoni di locazione finanziaria (es. leasing degli impianti).

Il costo totale dei fattori fissi prende il nome di “costo totale fisso”. Esso non varia al variare della quantità prodotta.

Il costo medio dei fattori fissi prende il nome di “costo medio fisso”. Esso diminuisce all’aumentare della quantità prodotta, perché viene a ripartirsi su un numero via via maggiore di unità.

Il costo totale dei fattori variabili prende il nome di “costo totale variabile”.

Sono esempi di costi per fattori variabili i salari, il costo delle materie prime utilizzate, dell’energia elettrica, dei combustibili, delle riparazioni ordinarie ecc. I costi variabili dipendono direttamente dal volume di produzione.

Il costo medio dei fattori variabili prende il nome di “costo medio variabile”.

Il costo totale è la somma dei costi totali fissi e dei costi totali variabili

Il costo medio è la somma dei costi medi fissi e dei costi medi variabili.

Il costo marginale è la variazione del costo totale conseguente alla variazione della quantità prodotta:

dove PT è una determinata quantità di prodotto.

La nozione matematica di costo marginale considera variazioni ∆PT molto piccole, vicine allo zero. Utilizzando un foglio elettronico normalmente, per ottenere la nozione matematica di costo marginale, si utilizzano variazioni dell’ordine di 0,00000000001.

La definizione matematica precisa è quella di “derivata della funzione di costo rispetto alla quantità prodotta”:

che si legge: “limite, per ∆PT che tende a zero, del rapporto tra la variazione di CT e della variazione di PT”

Nei testi didattici di economia, invece, viene considerato ∆PT = 1, in modo che la formula diventa:

Conformemente a questa formula, nei testi didattici il costo marginale di un dato fattore viene definito come “l’incremento dei costi totali per effetto della produzione di una unità in più di prodotto”

Noi utilizzeremo quest’ultima formula per calcolare il costo marginale

Consideriamo il breve periodo, in cui il fattore K è fisso (K = 5)

TABELLA 0603042101
PT	K	L	CT(PT)	CT(PT–1)	CTF(PT)	CTV(PT)	CMA(PT)	CME(PT)	CMEF(PT)	CMEV(PT)
5	5	0,11	40,44	40,28	40,00	0,44	0,15	8,08	8,00	0,08
10	5	0,44	41,76	41,44	40,00	1,76	0,32	4,17	4,00	0,17
15	5	1,00	44,00	43,48	40,00	4,00	0,52	2,93	2,66	0,26
20	5	1,77	47,08	46,40	40,00	7,08	0,68	2,35	2,00	0,35
25	5	2,77	51,08	50,24	40,00	11,08	0,83	2,04	1,60	0,44
30	5	4,00	56,00	54,92	40,00	16,00	1,08	1,86	1,33	0,53
35	5	5,44	61,76	60,52	40,00	21,76	1,23	1,76	1,14	0,62
40	5	7,11	68,44	67,00	40,00	28,44	1,44	1,71	1,00	0,71
45	5	9,00	76,00	74,40	40,00	36,00	1,59	1,68	0,88	0,80
50	5	11,11	84,44	82,68	40,00	44,44	1,75	1,68	0,80	0,88

Eseguiamo alcuni calcoli esemplificativi, tenendo presente che per ottenere la corrispondenza con la tabella vanno utilizzati valori di divisioni, moltiplicazioni o radici troncati a due cifre:

● Calcoliamo ad esempio CT(10)

Per far questo abbiamo bisogno di sapere quanto lavoro impiega l’imprenditore per produrre 10 unità di prodotto, tenendo conto che vengono utilizzate 5 unità di capitale (fattore fisso).

Per saperlo, occorre anzitutto risolvere rispetto ad L la formula della funzione di produzione:

ottenendo:

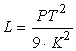
Quindi occorre sostituire in tale formula i valori dati di PT e di K, ottenendo:

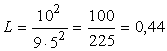
Il costo del lavoro impiegato per produrre 10 unità di prodotto è quindi pari a 0,44 ⋅ 4 = 1,76

Il costo del capitale impiegato per produrre 10 unità di prodotto è invece pari a 5 ⋅ 8 = 40

Il costo totale di 10 unità di prodotto è quindi di 41,76

● Calcoliamo ad esempio CTF(10)

Tenendo conto che vengono impiegate 5 unità di fattore fisso, ciascuna delle quali costa 8 € abbiamo che CTF(10) = 40 €

● Calcoliamo ad esempio CTV(10)

Tenendo conto che vengono impiegate 0,44 unità di lavoro (vedi sopra il calcolo di CT(10)) ciascuna del costo di 4 € abbiamo che CTV(10) = 0,44 ⋅ 4 = 1,76 €

● Calcoliamo ad esempio CMA(10)

Poiché CMA(10) = CT(10) – CT(9) e sappiamo che CT(10) = 41,76, occorre calcolare CT(9) con lo stesso sistema utilizzato per CT(10), ottenendo:

CT(9) = 41,44

e quindi:

CMA(10) = CT(10) – CT(9) = 41,76 – 41,44 = 0,32

● Calcoliamo ad esempio CME(10)

Il costo medio di 10 unità di prodotto è dato da:

● Calcoliamo ad esempio CMEF(10)

Tenendo conto che (vedi sopra) CTF(10) è pari a 5 ⋅ 8 = 40 € abbiamo:

● Calcoliamo ad esempio CMEV(10)

Tenendo conto che (vedi sopra) CTV(10) è pari a 1,76 € abbiamo:

Il profitto normale e l’extraprofitto

back to index

La nozione di costo per l’economista è alquanto differente di quella dell’addetto alla contabilità. L’economista considera un costo anche le spese che l’imprenditore risparmia grazie a fattori di sua proprietà (es. proprietà dei locali in cui esercita una impresa di ristorazione).

L’insieme dei ricavi che l’imprenditore potrebbe ottenere cedendo ad altre imprese l’uso dei fattori di sua proprietà che egli impiega nella propria impresa costituisce un insieme di costi che va sotto il nome di “profitto normale”.

Tra tali costi possiamo ricordare:

● Costi legati al lavoro dell’imprenditore nell’impresa. Per ogni ora di lavoro dirigenziale svolta dall’imprenditore viene contabilizzato un costo pari a quanto egli riceverebbe lavorando come direttore generale presso imprese di terzi

● Costi legati all’impiego di capitali dell’imprenditore. Viene contabilizzato un costo pari agli interessi che l’imprenditore ricaverebbe dando in prestito tali capitali a terzi

● Costi legati all’impiego di risorse naturali o beni immobili (es. edifici) di proprietà dell’imprenditore. Viene contabilizzato un costo pari al canone di locazione che l’imprenditore potrebbe ricavare cedendo a terzi l’uso di tali beni

● Costi legati all’impiego di beni strumentali di proprietà dell’imprenditore. Se l’imprenditore utilizza la propria auto per spostamenti aziendali si contabilizza un costo pari a ciò che potrebbe ottenere noleggiando l’auto a terzi.

● Costi legati all’impiego di brevetti di proprietà dell’imprenditore. Se l’imprenditore utilizza brevetti su proprie invenzioni viene contabilizzato un costo pari a quanto egli potrebbe ricavare concedendo a terzi lo sfruttamento dell’invenzione.

Tutto ciò che l’impresa guadagna oltre il profitto normale viene chiamato “extraprofitto” e coincide con la nozione comune di “profitto” a cui siamo abituati a pensare.

Calcoliamo, relativamente al breve periodo, il ricavo totale RT, il ricavo marginale RMA, il ricavo medio RME dell’impresa Alfa

back to index

Il ricato totale è dato dalla moltiplicazione:

Numero di unità vendute ⋅ prezzo di vendita

e cioè:

RT = PT ⋅ p

Il prezzo varia al variare della quantità prodotta dalla impresa, perché le famiglie accetteranno una data quantità solo al prezzo che esse ritengono conveniente, e aumenteranno i loro acquisti solo se il prezzo scende (vedi figura 0603080935):

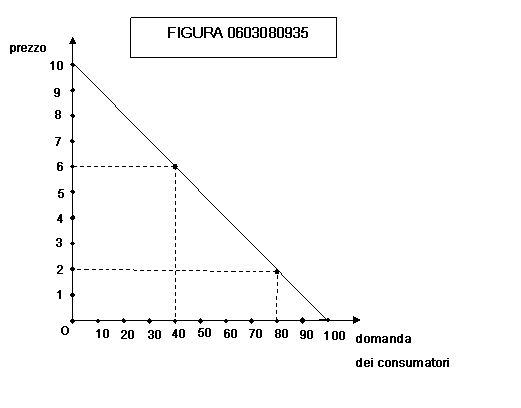
Dalla figura si vede che l’impresa potrà vendere 40 unità ad un prezzo di 6 €, realizzando un ricavo totale RT(60) = 240 €, ma potrà vendere 80 unità al prezzo più basso di 2 € realizzando un ricavo totale più basso RT(80) = 160 €

Il ricavo marginale è la variazione del costo totale conseguente alla variazione della quantità prodotta:

dove PT è una determinata quantità di prodotto.

La nozione matematica di ricavo marginale considera variazioni ∆PT molto piccole, vicine allo zero. Utilizzando un foglio elettronico normalmente, per ottenere la nozione matematica di ricavo marginale, si utilizzano variazioni dell’ordine di 0,00000000001.

La definizione matematica precisa è quella di “derivata della funzione di ricavo rispetto alla quantità prodotta”:

che si legge: “limite, per ∆PT che tende a zero, del rapporto tra la variazione di RT e della variazione di PT”

Nei testi didattici di economia, invece, viene considerato ∆PT = 1, in modo che la formula diventa:

Conformemente a questa formula, nei testi didattici il ricavo marginale di un dato fattore viene definito come “l’incremento dei ricavi totali per effetto della produzione di una unità in più di prodotto”

Noi utilizzeremo quest’ultima formula per calcolare il ricavo marginale

Consideriamo il breve periodo, in cui il fattore K è fisso (K = 5)

TABELLA 0603042236
PT	p	RT(PT)	RT(PT–1)	RMA(PT)	RME(PT)
5	9,50	47,50	38,40	9,10	9,50
10	9,00	90,00	81,90	8,10	9,00
15	8,50	127,50	120,40	7,10	8,50
20	8,00	160,00	153,90	6,10	8,00
25	7,50	187,50	182,39	5,11	7,50
30	7,00	210,00	205,89	4,11	7,00
35	6,50	227,50	224,39	3,11	6,50
40	6,00	240,00	237,89	2,11	6,00
45	5,50	247,50	246,39	1,11	5,50
50	5,00	250,00	249,89	0,11	5,00

Eseguiamo alcuni calcoli esemplificativi, tenendo presente che per ottenere la corrispondenza con la tabella vanno utilizzati valori di divisioni, moltiplicazioni o radici troncati a due cifre:

● Calcoliamo ad esempio RT(10)

Per far questo abbiamo bisogno di sapere qual è il prezzo al quale i consumatori sono disposti ad acquistare 10 unità di prodotto.

Data la funzione di domanda dei consumatori:

Domanda = 100 – Prezzo * 10

risolvendo per il prezzo otteniamo:

da cui, inserendo il valore della domanda (10) otteniamo:

Moltiplicando il prezzo unitario di 9 € per la quantità di unità vendute (10 unità) otteniamo un ricato totale RT(10) = 90 €

● Calcoliamo ad esempio RMA(10)

Poiché RMA(10) = RT(10) – RT(9), calcoliamo, come visto sopra, i due valori:

RT(10) = 90

RT(9) = 81,90

e dalla loro differenza otteniamo:

RMA(10) = 90 – 81,9 = 8,10

● Calcoliamo ad esempio RME(10)

Il ricavo medio di 10 unità di prodotto è dato da:

Calcoliamo, relativamente al breve periodo, il profitto totale PRT, il profitto marginale PRMA, il profitto medio PRME dell’impresa Alfa

back to index

Il profitto marginale è la variazione del profitto totale conseguente alla variazione della quantità prodotta:

dove PT è una determinata quantità di prodotto.

La nozione matematica di profitto marginale considera variazioni ∆PT molto piccole, vicine allo zero. Utilizzando un foglio elettronico normalmente, per ottenere la nozione matematica di profitto marginale, si utilizzano variazioni dell’ordine di 0,00000000001.

La definizione matematica precisa è quella di “derivata della funzione di profitto rispetto alla quantità prodotta”:

che si legge: “limite, per ∆PT che tende a zero, del rapporto tra la variazione di PRT e della variazione di PT”

Nei testi didattici di economia, invece, viene considerato ∆PT = 1, in modo che la formula diventa:

Conformemente a questa formula, nei testi didattici il profitto marginale di un dato fattore viene definito come “l’incremento dei profitti totali per effetto della produzione di una unità in più di prodotto”

Noi utilizzeremo quest’ultima formula per calcolare il profitto marginale

Consideriamo il breve periodo, in cui il fattore K è fisso (K = 5)

TABELLA 0603042249
PT	RT	CT	PRT	RMA	CMA	PRMA	PRME
5	47,50	40,44	7,06	9,10	0,15	8,95	1,41
10	90,00	41,76	48,24	8,10	0,32	7,78	4,82
15	127,50	44,00	83,50	7,10	0,52	6,58	5,56
20	160,00	47,08	112,92	6,10	0,68	5,42	5,64
25	187,50	51,08	136,42	5,11	0,83	4,28	5,45
30	210,00	56,00	154,00	4,11	1,08	3,03	5,13
35	227,50	61,76	165,74	3,11	1,23	1,88	4,73
40	240,00	68,44	171,56	2,11	1,44	0,67	4,28
45	247,50	76,00	171,50	1,11	1,59	-0,48	3,81
50	250,00	84,44	165,56	0,11	1,75	-1,64	3,31

Eseguiamo alcuni calcoli esemplificativi, tenendo presente che per ottenere la corrispondenza con la tabella vanno utilizzati valori di divisioni, moltiplicazioni o radici troncati a due cifre:

Per calcolare il profitto totale di 10 unità PRT(10) sottraiamo al ricavo totale di 10 unità il costo totale di 10 unità:

PRT(10) = RT(10) – CT(10) = 90 – 41,76 = 48,24

Per calcolare il profitto marginale della decima unità PRMA(10) sottraiamo al ricavo marginale della decima unità RMA(10) il costo marginale della decima unità CMA(10):

PRMA(10) = RT(10) – CMA(10) = 8,10 – 0,32 = 7,78

Il profitto medio di 10 unità PRME(10) si ottiene dalla formula:

Le curve di breve periodo della impresa tipica e i loro rapporti

back to index

Analizziamo la situazione dell’impresa nel breve periodo (cosiddetta “analisi di breve periodo”).

La legge dei rendimenti decrescenti dei fattori dice che nel breve periodo ad incrementi del fattore o fattori variabili corrisponderanno incrementi sempre minori (= meno che proporzionali) della produzione. Un esempio tipico si ha con le risorse naturali che, nel periodo breve non sono aumentabili: aumentando la flotta dei pescherecci aumenta di poco o al limite non aumenta il pescato.

Come si vede dalla figura 0603051136 la legge dei rendimenti decrescenti si riferisce all’andamento della produttvità marginale a partire dal punto A. Normalmente una impresa che nel breve periodo vuole espandere la produzione si trova oltre il punto A, anche se in qualche caso imprese con grandi impianti non utilizzati possono per lungo tempo operare in una situazione di rendimenti crescenti (zona prima del punto A).

La legge dei rendimenti decrescenti dei fattori non ha a che fare con la disponibilità limitata di risorse naturali, perché esse possono essere aumentate nel lungo periodo.

Dal rendimento (= produttività marginale) decrescente del fattore variabile deriva, come si vede dalla figura 0603051136 l’andamento prima più che proporzionale poi meno che proporzionale e infine decrescente del grafico del prodotto totale. Fino al punto B la produzione cresce a ritmo crescente; dal punto B al punto C la produzione aumenta a ritmo decrescente; dal punto C in poi la produzione diminuisce.

A partire dal punto B (cioè oltre il settimo lavoratore impiegato o, a seconda delle unità di misura scelte, della settima ora di lavoro impiegata) il prodotto totale non aumenta, ma anzi inizia a diminuire.

Dal rendimento (= produttività marginale) decrescente del fattore variabile deriva anche, nel breve periodo, la tipica forma dei costi “a scodella”.

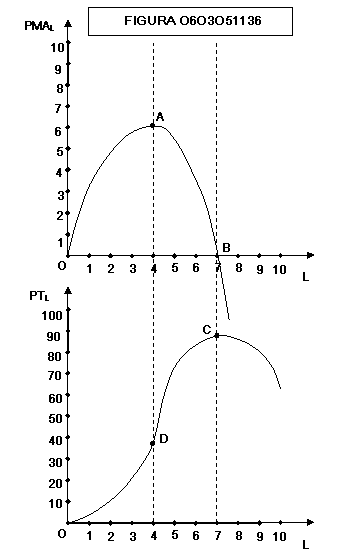
Per spiegare la legge dei rendimenti decrescenti del fattore variabile facciamo l’esempio di un cantiere edile dove sono impiegati dieci operai. Volendo espandere la produzione (per esempio, accelerare la costruzione di uno stabile), vengono impiegati via via altri oprai. La produzione allora manifesta un andamento crescente, ma il ritmo con cui cresce è progressivamente declinante: la produzione del cantiene aumenta in misura meno che proporzionale rispetto all’aumento degli operai occupati. Ciò si verifica perché, all’aumentare delle unità lavorative in uno stesso posto di lavoro, ci si allontana gradatamente dalla “dimensione ottima”: il lavoro diviene più difficilmente gestibile, i controlli sono più sporadici e così via Si perde, insomma, una certa razionalizzazione della produzione. Se nel cantiene venissero impiegati ulteriori operai, prima o poi si arriverebbe a un punto di “saturazione”. I lavoratori utilizzati finirebbero per ostacolarsi nello svolgimento delle proprie mansioni, creando le premesse per un rallentamento della produzione. Da una crescita della produzione, sia pure a ritmo decrescente, si passerebbe a una diminuzione della produzione. E’ questa la fase in cui la produttività marginale diviene prima nulla, poi negativa.

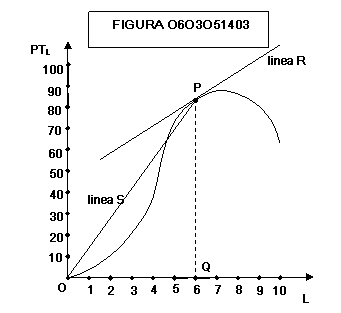
La nozione matematica di prodotto marginale PMA_L(6) relativo ad una produzione ottenuta con 6 unità di prodotto è la pendenza della linea R tangente nel punto P.

La nozione matematica di prodotto medio PME_L(6) ottenuto con l’impiego di 6 unità di fattore lavoro è la inclinazione della linea S, che unisce l’origine al punto P

Dalla figura 0603051209 possiamo vedere che anche il prodotto o produttività media, per la stessa legge dei rendimenti marginali decrescenti dei fattori è prima crescente poi decrescente fino a diventare negativo

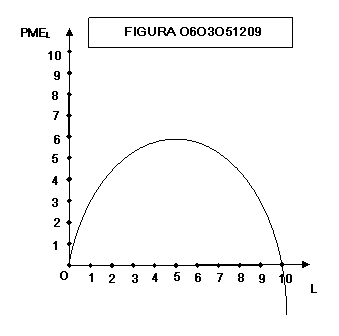
Dal rendimento (= produttività marginale) decrescente del fattore variabile deriva anche, nel breve periodo, la tipica forma dei costi a scodella e la conseguente forma della linea di costo totale (fig. 0603051152).

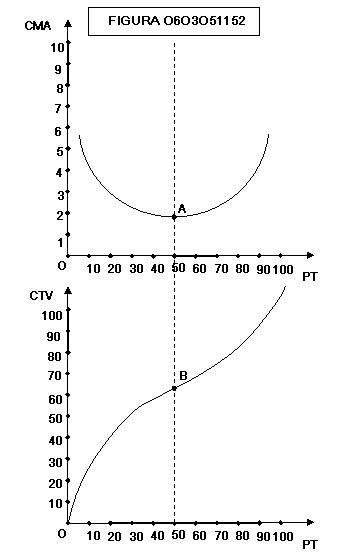
Come si vede dalla figura 0603051152 se i costi marginali decrescenti (a sinistra della linea tratteggiata) i costi crescono meno che proporzionalmente rispetto alla produzione (la pendenza della linea di costo è decrescente), mentre se i costi marginali sono crescenti (a destra della linea tratteggiata) i costi crescono più che proporzionalmente rispetto alla produzione (pendenza crescente della linea di costo).

Se, per ogni livello di produzione PT sommiamo il costo totale fisso col costo totale variabile otteniamo il grafico di figura 0603051355:

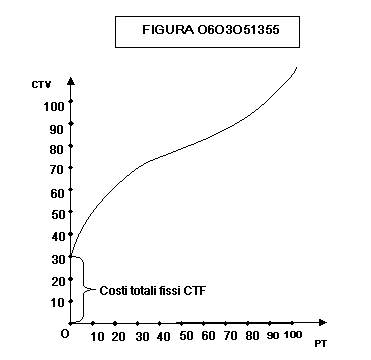
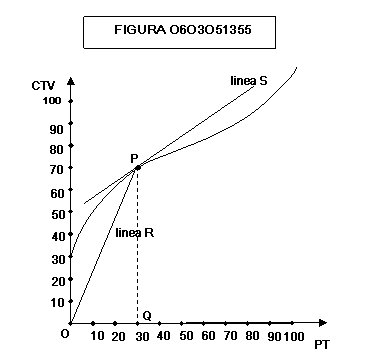
La nozione matematica di costo marginale relativo ad un prodotto OQ di 30 unità è data dalla pendenza della retta S, mentre la nozione matematica di costo medio relativo a 30 unità di prodotto è data dalla pendenza della retta R (fig. 060305 1355).

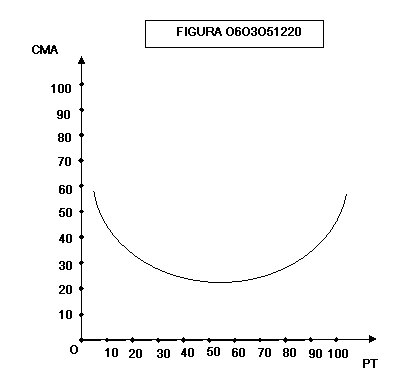
Le figura 0603051220 mostra l’andamento del costo medio fisso: aumentando le unità prodotte i costi fissi vengono ripartiti su un numero sempre maggiore di unità e quindi diminuiscono.

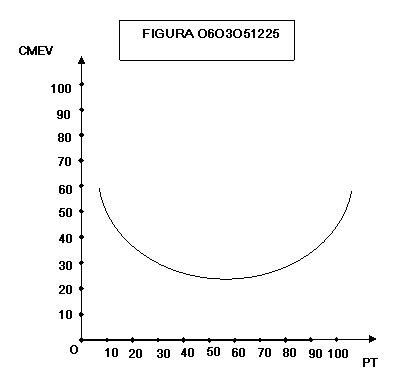
La figura 0603051225 mostra l’andamento del costo medio variabile: anch’esso, per la legge dei rendimenti decrescenti del fattore variabile, ha una forma a scodella.

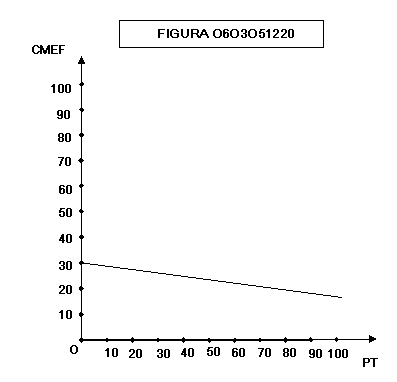
Anche la curva del costo marginale (fig. 0603051220) per la legge dei rendimenti decrescenti del fattore variabile ha forma a scodella.

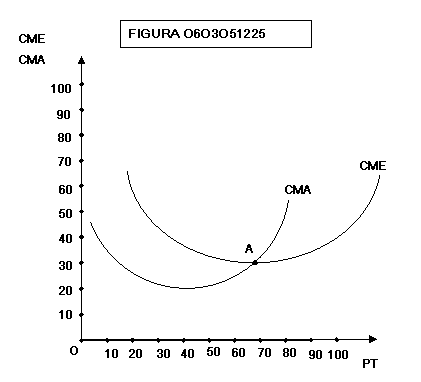
L’esatta posizione reciproca delle due curve CMA e CME è mostrata nella figura 0603051225. Come si può vedere, in tutti i punti in cui il costo medio è sopra il costo marginale il costo medio decresce; in tutti i punti in cui il costo medio è al disotto del costo marginale il costo medio cresce; Nel punto in cui i due costi sono uguali, il costo medio tocca un valore minimo.

Le curve di costo di lungo periodo dell’impresa tipica

back to index

Nel lungo periodo si suppone che tutti i fattori produttivi diventino variabili.Mentre il costo totale di breve periodo viene ottenuto considerando, per ciascun livello produttivo una sola combinazione di fattori, quella che l’imprenditore è costretto a scegliere avendo un fattore fisso (almeno nel caso in cui esista un solo fattore variabile), nel caso dei costi totali di lungo periodo il costo, per ciascun livello di produzione, è dato dalla combinazione ottima dei fattori.

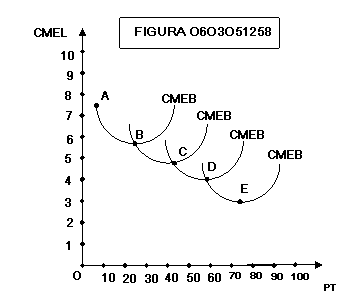
La curva di costo medio di lingo periodo CMEL è ottenuta dalle curve di costo medio di breve periodo, che in questo paragrafo chiameremo CMEB.

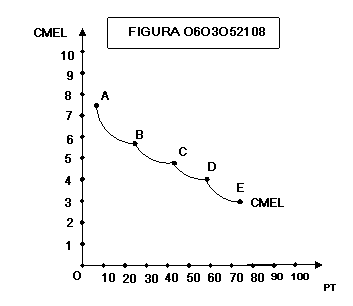
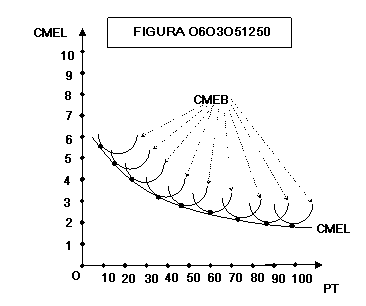
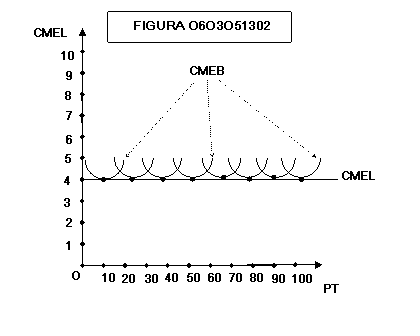
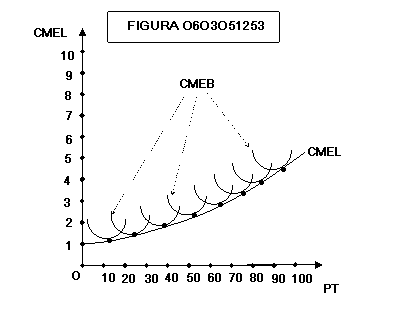
La figura 0603051258 e la figura 0603052108 mostrano come la curva CMEL dei costi medi di lungo periodo sia costituita dai tratti discendenti delle curve di costo di breve periodo. All’aumentare del numero delle curve di costo di breve periodo considerato si ottengono le figure 0603051250, 0603051302 e 0603051253 rispettivamente per il caso di rendimenti di scala decrescenti, costanti e crescenti.

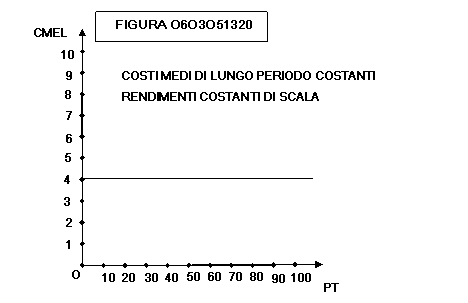
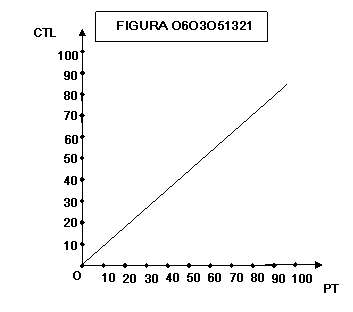
Le figure 0603051320 e 0603051321 mostrano come una impresa che nel lungo periodo incontra rendimenti costanti di scala (il prodotto cresce in proporzione alla crescita della quantità impiegata dei fattori) ha una curva di costo medio di lungo periodo CMEL costante (parallela all’asse orizzontale), che corrisponde ad un andamento rettilineo dei costi totali CTL

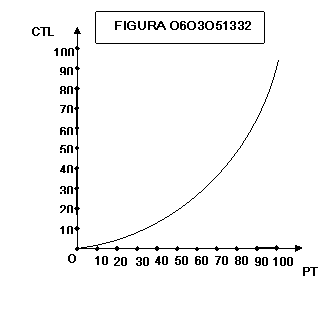
Le figure 0603051329 e 0603051330 mostrano come una impresa che nel lungo periodo incontra rendimenti crescenti di scala (il prodotto cresce più che proporzionalmente rispetto alla crescita della quantità impiegata dei fattori) ha i costi medi di lungo periodo CMEL che diminuiscono, ciò che corrisponde ad un andamento rettilineo dei costi totali CTL a pendenza via via decrescente

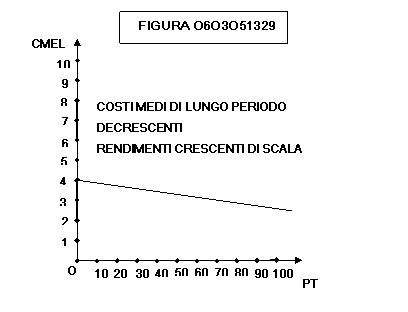
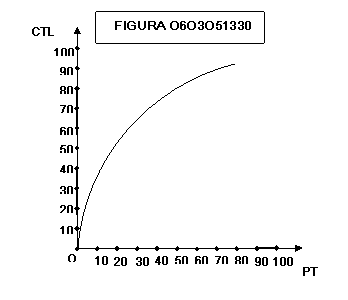
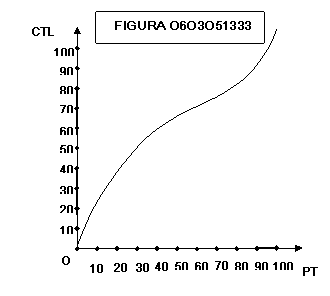
Le figure 0603051331 e 0603051332 mostrano come una impresa che nel lungo periodo incontra rendimenti decrescenti di scala (il prodotto cresce meno che proporzionalmente rispetto alla crescita della quantità impiegata dei fattori) ha i costi medi di lungo periodo CMEL che aumentano, ciò che corrisponde ad un andamento dei costi totali CTL a pendenza via via crescente.

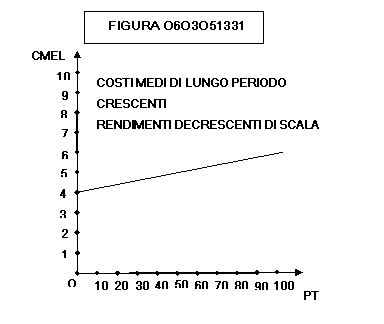
Si noti che i costi totali partono dall’origine, a differenza che nel caso di breve periodo, perché tutti i fattori possono essere variati, e quindi ad una produzione zero non ci sono fattori fissi, cosicché il costo è zero.

Le curve di costo di lungo periodo dell’industria concorrenziale

back to index

Nel lungo periodo, se il prezzo è superiore ai costi delle imprese, nuove imprese entreranno nel mercato facendo aumentare la produzione e diminuire il prezzo.

Se il prezzo diviene invece inferiore ai costi delle imprese, le imprese ultramarginali usciranno dal mercato facendo diminuire la produzione ed aumentare il prezzo.

Entrambi questi meccanismi garantiscono che il costo medio di lungo periodo sia pari al costo medio.

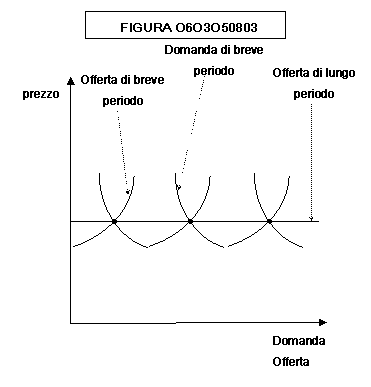
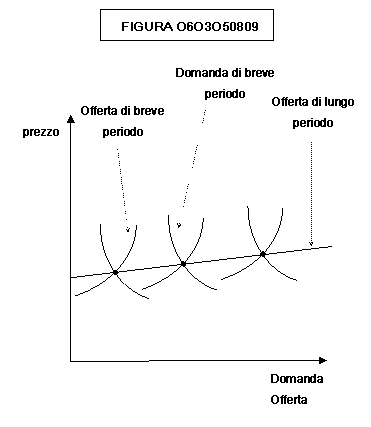
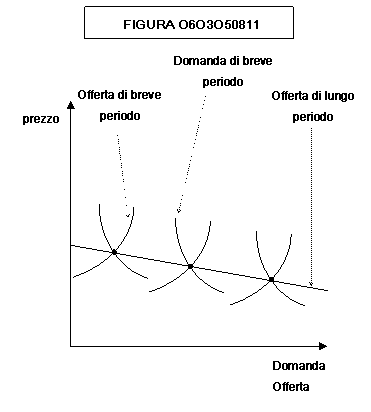
Nelle figure 0603060803, 0603060809, 0603060811 vengono mostrate le curve di offerta di lungo periodo rispettivamente per una industria a costi costanti, crescenti o decrescenti. Mano a mano che aumenta la domanda sia la curva di offerta che la curva di domanda di breve periodo si spostano, dando luogo ai punti che formano la curva di offerta di lungo periodo.