❍ LE
UTILITA’
Utilità (primo
significato) è la qualità di un bene che è in grado di soddisfare un bisogno
Utilità (secondo
significato) è il grado di soddisfazione del bisogno ottenuto tramite il
consumo di un bene o di un servizio
Utile è
il bene capace di soddisfare un bisogno
Utilità totale (UT) è la somma di tutte le utilità ricavate dalle dosi
consumate
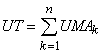
che si legge: “sommatoria, per k che varia da 1 ad n di UMAk
UTn si
legge: “Utilità totale ricavata dal consumo di n dosi di bene”
Utilità marginale è l’utilità fornita dall’ultima dose di bene
consumata
UMAn = UTn – UTn-1
UMAn si
legge: “Utilità marginale ricavata dal consumo della n-esima dose di bene”
Utilità media è
l’utilità che si ricava in media da ogni dose di n consumate
![]()
UMEn si
legge: “Utilità media ricavata dal consumo di n dosi di bene”
Utilità marginale ponderata
(UMAP) è
l’utilità che fornisce ciascun centesimo di € speso per acquistare una
determinata dose
![]()
UMAPn si
legge: “Utilità marginale ponderata riferita alla n-esima dose di bene”
Come si è già detto nelle lezioni introduttive, il concetto di
“utilità” è diverso rispetto all’uso comune. Per l’economista "bene utile”
non significa “bene il cui consumo è particolarmente vantaggioso per gli
interessi di una persona”. Anche la droga che un drogato paga, o la figurina
che il bambino acquista all’edicola, o il gel per i capelli sono utili per
l’economista. Il ciottolo in cui il selvaggio crede sia contenuto il sortilegio
che guarirà dalla febbre è “utile” per lui.
“Utilità” non è neanche sinonimo di piacere fisico o psicologico:
anche la chemioterapia dell’ammalato di cancro o l’amputazione d’urgenza senza
anestesia sono “utili”.
❍ IL PREZZO
Il prezzo è il numero di unità di moneta che si scambia con un
determinato bene.
Questa è la definizione di “prezzo assoluto”. Per “prezzo
relativo” del bene A rispetto al bene B si intende il numero di unità di bene B
che si scambiano con una unità di bene A.
Il prezzo relativo è legato al prezzo assoluto dalla formula:
![]()
❍ I GRAFICI
DELLE UMA E DELLE UT
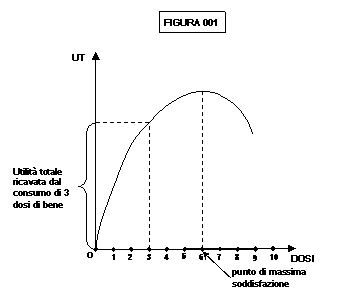
Come si nota dal grafico, per la legge della sazietà, dopo la
sesta dose, che rende massima la soddisfazione del consumatore, la settima dose
fornisce disutilità (disgusto), e quindi la soddisfazione totale si abbassa. Si
pensi ad una persona assetata che, bevuto il sesto bicchiere d’acqua rifiuta
altri bicchieri; se una tale persona continuasse a bere proverebbe disgusto e
questo abbasserebbe l’utilità totale che aveva sinora ricavato dal consumo
delle precedenti dosi di acqua.
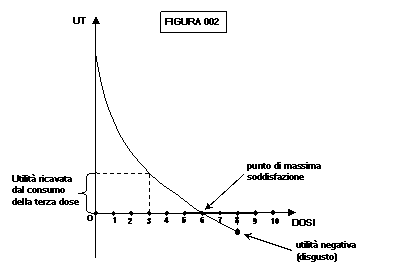
Come si vede dal grafico, per la legge della sazietà (chiamata
anche legge delle utilità marginali descrescenti) dosi successive di un bene
apportano una utilità sempre minore, fino a quando la settima dose apporta
disutilità (disgusto)
Perché la curva delle UT, fino alla settima dose, ha la forma del
grafico di un rapporto diretto ad inclinazione decrescente in valore assoluto
(figura 003) e non la forma del grafico di un rapporto diretto ad inclinazione
costante (figura 004) o di un rapporto diretto ad inclinazione crescente
(figura 005)?



Per capire questo, dobbiamo visualizzare le utilità marginali
(UMA) nel grafico delle utilità totali (UT):
O 8 UT 9 10 7 6 5 4 3 2 1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Si tratta delle stesse frecce che possono essere visualizzate nel
grafico delle utilità marginali (UMA):
10 9 8 O 1 2 3 4 5 6 7 DOSI![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

❍ LA SCELTA DI UN CONSUMATORE TRA DUE BENI AVENTI
LO STESSO PREZZO E CON DOSI NON FRAZIONABILI
Supponiamo che il sig. Rossi abbia la somma di 10 € e debba
scegliere quanta carne e quanta verdura acquistare.
Il costo di una dose (ettogrammo) di carne è di 1 €; il costo di
una dose (ettogrammo) di verdura è di 1 €
Nel gergo economico, si definisce paniere una combinazione di una
data quantità di ciascun bene disponibile. Il sig. Rossi può scegliere tra i
seguenti panieri:
● 0 dosi di carne + 10 dosi di verdura
● 1 dose di carne + 9 dosi di verdura
● 2 dosi di carne + 8 dosi di verdura
● 3 dosi di carne + 7 dosi di verdura
● 4 dosi di carne + 6 dosi di verdura
● 5 dosi di carne + 5 dosi di verdura
● 6 dosi di carne + 6 dosi di verdura
● 7 dosi di carne + 3 dosi di verdura
● 8 dosi di carne + 2 dosi di verdura
● 9 dosi di carne + 1 dose di verdura
● 10 dosi di carne + 0 dosi di verdura
Supponiamo che le utilità siano le seguenti:
|
DOSI |
UT carne |
UT verdura |
UMA carne |
UMA verdura |
|
1 |
100 |
120 |
100 |
120 |
|
2 |
190 |
220 |
90 |
100 |
|
3 |
270 |
300 |
80 |
80 |
|
4 |
340 |
360 |
70 |
60 |
|
5 |
400 |
400 |
60 |
40 |
|
6 |
450 |
420 |
50 |
20 |
|
7 |
490 |
430 |
40 |
10 |
|
8 |
520 |
435 |
30 |
5 |
|
9 |
540 |
438 |
20 |
3 |
|
10 |
550 |
440 |
10 |
2 |
(Lo studente dovrebbe imparare a riempire da solo le caselle delle
UT conoscendo le UMA e viceversa)
Il sig. Rossi, essendo un soggetto razionale (homo oeconomicus ) spenderà ciascuno dei dieci euro scegliendo ogni
volta le dosi che gli forniscono l’utilità più alta.
Egli sceglierà pertanto, nell’ordine:
● la prima dose di verdura
● la prima dose di carne (o la seconda dose di
verdura)
● la seconda dose di verdura (o la prima dose di
carne)
● la terza dose di carne
● la terza dose di verdura (o la quarta dose di
carne)
● la quarta dose di carne (o la terza dose di
verdura
● la quarta dose di carne
● la quarta dose di verdura (o la quinta dose di
carne)
● la quinta dose di carne (o la quarta dose di
verdura)
● la sesta dose di carne
Il paniere scelto da Rossi sarà quindi composto da 6 dosi di carne
+ 4 dosi di verdura
❍ LA SCELTA DI UN CONSUMATORE TRA DUE BENI AVENTI
PREZZI DIVERSI E CON DOSI NON FRAZIONABILI
Supponiamo che il sig. Rossi abbia la somma di 10 € e debba
scegliere quanta carne e quanta verdura acquistare.
Il costo di una dose (ettogrammo) di carne è di 2 €; il costo di
una dose (ettogrammo) di verdura è di 1 €
Poiché i prezzi sono diversi, non possiamo utilizzare, per la
scelta, le utilità marginali (UMA), ma dobbiamo calcolare le utilità marginali
ponderate (UMAP):
|
DOSI |
UT carne |
UT verdura |
UMA carne |
UMA
verdura |
UMAP carne (per
centesimo di €) |
UMAP
verdura (per
centesimo di €) |
|
1 |
100 |
120 |
100 |
120 |
0,5 |
1,2 |
|
2 |
190 |
220 |
90 |
100 |
0,45 |
1 |
|
3 |
270 |
300 |
80 |
80 |
0,4 |
0,8 |
|
4 |
340 |
360 |
70 |
60 |
0,35 |
0,6 |
|
5 |
400 |
400 |
60 |
40 |
0,3 |
0,4 |
|
6 |
450 |
420 |
50 |
20 |
0,25 |
0,2 |
|
7 |
490 |
430 |
40 |
10 |
0,2 |
0,1 |
|
8 |
520 |
435 |
30 |
5 |
0,15 |
0,05 |
|
9 |
540 |
438 |
20 |
3 |
0,1 |
0,03 |
|
10 |
550 |
440 |
10 |
2 |
0,05 |
0,02 |
Il sig. Rossi, per stabilire se acquistare come prima dose verdura
o carne noterà che mentre un centesimo di euro (che d’ora in poi per brevità
chiameremo cent) speso per la prima dose di carne fornisce una utilità di 0,5,
un cent speso per l’acquisto della prima dose di verdura fornisce una utilità
di 1,2: egli pertanto acquisterà come prima dose la verdura.
Per ogni dose successiva egli ripete il ragionamento, tenendo
presenti le utilità marginali ponderate (UMAP) e non le utilità marginali
(UMA).
❍ LA SCELTA DI UN CONSUMATORE TRA DUE BENI AVENTI
PREZZI DIVERSI E CON DOSI FRAZIONABILI: LA LEGGE DELL’EGUAGLIANZA DELLE UTILITA’
MARGINALI PONDERATE
Supponiamo ora che il Sig. Rossi abbia 10 € e che il prezzo di una
dose di carne sia di 2 € mentre quello della verdura sia di 1 €, ma che, a
differenza del caso precedente, egli possa scegliere di frazionare fino ai
grammi (o ai milligrammi, o ai microgrammi…) la dose di carne e quella di
verdura acquistate. In altre parole, egli non dovrà acquistare una quantità di
carne o di verdura che sia multipla di 1 ettogrammo.
In questo caso le tabelle precedenti non ci aiutano nella scelta,
e occorre riferirsi al grafico sottostante:

Ogni punto dell’asse orizzontale rappresenta un centesimo (cent)
di spesa in carne o verdura. Il grafico può essere letto sia da sinistra (allora
la curva sarà la curva A, che esprime per ogni cent speso in carne la utilità
che se ne ricava) o da sinistra (allora la curva sarà la curva B, che esprime
per ogni cent speso in verdura la utilità che se ne ricava.
Proviamo ad isolare una sola curva per vedere meglio come si legge
il grafico delle UMAP:

Ad ogni punto (cent) sull’asse orizzontale corrisponde sull’asse
verticale l’utilità che questo ha procurato al consumatore. Ad esempio,
considerando il punto A, che corrisponde al 400° cent speso in carne, vediamo
che esso fornisce una utilità che può essere letta sull’asse verticale (OC) o
direttamente sopra il punto (AB).
Se tracciamo, segmento dopo segmento, tutte le utiltà dei
centesimi compresi tra il punto D e il punto G avremo colorato un’area che
rappresenta le utilità totali fornite dal 6° e dal 7° euro speso in carne. Ma
torniamo ad esaminare, in figura 010, i due grafici congiunti:

Ogni punto dell’asse orizzontale rappresenta anche una
combinazione possibile (paniere) di carne + verdura: ad es. il punto P
rappresenta una combinazione di 8 € di carne e 2 € di verdura.
Supponiamo che il sig. Rossi acquisti 8 € di carne e 2 € di
verdura. Il paniere scelto dal sig. Rossi è quello indicato dal punto N. L’area
della utilità totale ricavata dai due € di verdura sarà NGHM; l’area delle
utilità totali ricavate dagli 8 € di carne sarà ADPN. Se coloriamo le due aree,
vedremo che rimane bianca l’area BMP:
![]()

Dalla figura 011 vediamo che, se il sig. Rossi avesse scelto
invece il paniere corrispondente al punto C egli avrebbe potuto “colorare”
tutta l’area sotto le due curve. Il punto in cui si massimizza (massimizzare =
rendere più alto possibile) la utilità totale è quindi C
Ma in corrispondenza del punto C l’UMAP dell’ultimo centesimo
speso in carne (segmento BC) è identica all’UMAP dell’ultimo centesimo speso in
verdura (segmento BC): possiamo perciò riformulare in questo modo la regola da
seguire per massimizzare le proprie utilità totali: occorre consumare tanta
carne e tanta verdura che le rispettive utilità marginali ponderate si
eguaglino.
Questa regola è un importante risultato dell’analisi economica, e
prende il nome di legge dell’eguaglianza delle utilità marginali ponderate.
L’alunno dovrebbe accertarsi di saper rispondere alle seguenti
domande:
● Qual è il segmento verticale che rappresenta
l’utilità del 200° cent speso in carne?
● Qual è il segmento verticale che rappresenta
l’utilità del 300° cent speso in verdura?
● Qual è l’area che rappresenta le utilità
totali ricavate dal primo € speso in carne?
● Qual è l’area che rappresenta le utilità
totali ricavate da 3 € spesi in carne?
● Qual è l’area che rappresenta le utilità
totali ricavate dal 2° euro speso in carne?
❍ LE CURVE
DI INDIFFERENZA
Osserviamo la figura 012:
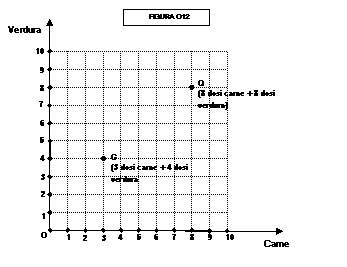
Sull’asse orizzontale misuriamo le dosi di carne, sull’asse
verticale le dosi di verdura. Ciascun punto dell’area compresa tra gli assi
rappresenta una combinazione (paniere) carne-verdura. Ad esempio, il punto P
rappresenta il paniere contenente 3 dosi di carne e 4 dosi di verdura, che
(supponiamo) gli forniscono 80 utilità; il punto Q rappresenta il paniere
contenente 8 dosi di carne e 8 dosi di verdura, che (supponiamo) gli forniscono
150 utilità.
Ad ogni punto può essere associata una utilità: quella del paniere
che esso rappresenta. Ad esempio possiamo supporre che il punto P
Definiamo curva di indifferenza la linea che unisce tutti i punti
che rappresentano combinazioni che forniscono la stessa utilità totale.
Proviamo a tracciare in figura 013 la curva di indifferenza nel
caso molto particolare di un individuo che ricava dalle dosi consumate sempre
la stessa utilità:
|
DOSI |
UMA carne |
UMA
verdura |
|
1 |
100 |
50 |
|
2 |
100 |
50 |
|
3 |
100 |
50 |
|
4 |
100 |
50 |
|
5 |
100 |
50 |
|
6 |
100 |
50 |
|
7 |
100 |
50 |
|
8 |
100 |
50 |
|
9 |
100 |
50 |
|
10 |
100 |
50 |
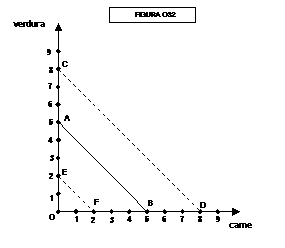
Partiamo dal punto A, che rappresenta una combinazione di 2 dosi
di carne + 10 dosi di verdura e fornisce quindi una utilità totale di 700
utilità.
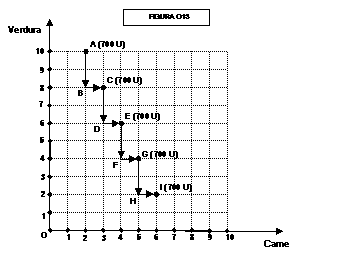
Se passiamo dal punto A al punto B perdiamo due dosi di verdura
(-100 utilità) passando da 700 a 600 utilità. Se però ci spostiamo dal punto B
al punto C ritroviamo un’altra combinazione che ci fornisce 700 utilità.
Proseguendo secondo questo metodo passiamo successivamente per i punti D, E, F,
G, H, I, e troviamo che i punti A, C, E, G, I rappresentano combinazioni che
forniscono tutte una utilità di 700. Troviamo anche che i punti B, D, F, H
rappresentano combinazioni che forniscono una utilità di 600.
Unendo le due serie di punti otteniamo nella figura 014 due curve
di indifferenza diverse, una caratterizzata da una utilità totale di 700 e una
caratterizzata da una utilità totale di 600:
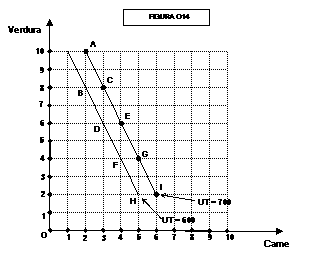

Le curve di indifferenza di un consumatore normale, però, non sono
segmenti retti: esse risentono dell’”effetto sazietà”.
Per l’effetto-sazietà, la riduzione di due dosi di verdura sottrae
una utilità sempre maggiore al paniere mentre, sempre per lo stesso effetto,
l’aggiunta di due dosi di carne apporta una utilità sempre più bassa.
Considerando per semplicità solo questo secondo fatto (l’aggiunta
di due dosi di carne apporta una utilità sempre più bassa), è evidente che i
segmenti BC, DE, FG e HI nella figura 013 devono allungarsi sempre di più (=
occorre una maggiore quantità di carne, che è divenuta meno utile) per
compensare la perdita di utilità dovuta alla diminuzione di verdura.
Le curve di indifferenza avranno quindi normalmente l’andamento di
figura 015:
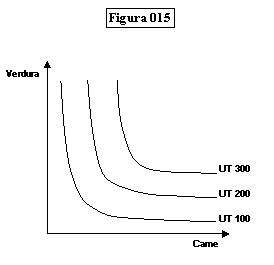
Lo studente dovrebbe verificare la sua comprensione delle curve di
indifferenza indicando quali dei grafici sotto indicati sono impossibili, e
perché:




❍ LE CURVE DI INDIFFERENZA COME CURVE DI LIVELLO
E LA FUNZIONE DI COBB-DOUGLAS
La funzione:
U = a ⋅ xb
⋅ yc
dove x e y sono le dosi consumate di due diversi beni e b + c = 1
si è una funzione di Cobb-Douglas .
Essa è anche definibile, tecnicamente, come una curva di livello.
Le curve di livello sono tipici modi di rappresentazione
matematica di una curva nello spazio bi- o tridimensionale che lo studente
incontra ad es. nello studio delle coniche: è noto che il luogo dei punti che
soddisfano l’equazione:
x2 + y2 = k
rappresentano la circonferenza con centro nell’origine e raggio k.
Variando k si ottengono le varie curve di livello per k = 1 (circonferenza con
raggio 1), k = 2 (circonferenza di raggio √2) ecc.
Le curve di livello sono tipi di rappresentazioni di curve
alternativi alla rappresentazione parametrica di una curva. Nella
rappresentazione parametrica il valore di ciascuna coordinata è fornito da una
distinta funzione di uno stesso parametro t:
x = x(t)
y = y(t)
quando t varia in un dato intervallo di R (es. l’intervallo [0,1])
viene descritta una corrispondente curva in R2.
Tornando all’altro modo di rappresentazione, la ragione della
definizione “curve di livello” è semplice. Se visualizziamo i risultati della
funzione x2 + y2 sull’asse verticale z di un grafico
tridimensionale otteniamo, per ogni coppia (x,y) sul piano x-y un valore
sull’asse z, in modo che la funzione è visualizzabile come un velo o superficie
tridimensionale che si sviluppa sopra il piano x-y e la cui distanza da tale
piano è, punto per punto, data dal valore della funzione. Unendo tutti i punti
del piano x-y che hanno sopra di sé la superficie ad una distanza
predeterminata otteniamo le curve di livello utilizzate in topografia per
descrivere in una cartina bidimensionale una superficie tridimensionale come
una montagna o una collina.
Normalmente a scuola lo studente incontra un solo tipo di curva di
livello, quello dato dal valore zero:
f(x,y) = 0
ma potrebbero benissimo essere studiate curve con valori
arbitrari:
f(x,y) = k
Una funzione come U = a ⋅ xb ⋅ yc fornisce, nel grafico
bidimensionale con x e y grandezze agli assi, le curve di indifferenza,
ciascuna delle quali è in realtà una curva di livello per una data utilità U:
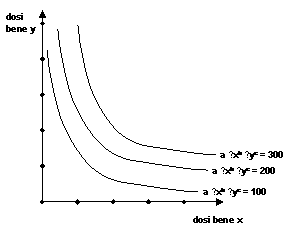
Una funzione come quella di Cobb-Douglas è omogenea di grado 1.
Una funzione f(x,y) si definisce omogenea di grado α se si ha:
f(n ⋅ x , n ⋅ y) = nα ⋅ f(x , y)
cioè se moltiplicando per n i valori delle variabili si ottiene nα volte il
valore della funzione originaria.
Poiché la funzione di Cobb-Douglas è omogenea di grado 1 si ha:
a ⋅ n ⋅ xb ⋅ n ⋅ yc = n ⋅ (a ⋅ xb ⋅ yc)
cioè, aumentando di n volte le dosi di entrambi i beni l’utilità
aumenta di n volte.
Ma questa non è una ipotesi plausibile, data la legge delle
utilità marginali decrescenti del consumatore. Una funzione più realistica
dovrebbe essere omogenea di grado inferiore ad 1.
Se lasciamo cadere la condizione circa gli esponenti nella funzione
di Cobb-Douglas:
b + c = 1
otteniamo tre tipi di funzioni:
▸ Per b + c = 1 la funzione a ⋅ xb ⋅ yc è omogenea di
grado 1: questo vuol dire che se aumenta di n volte la quantità di entrambi i
beni consumati l’utilità aumenta esattamente n volte. Il grafico delle curve di
indifferenza è allora il seguente:
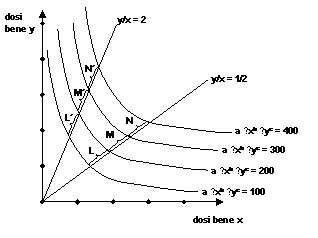
(le linee y/x = ½ e y/x = 2 sono linee lungo le quali è costante
il rapporto tra la quantità di x e la quantità di y consumata)
Come si vede, le distanze L, M, N (L’, M’, N’) tra successive
curve di indifferenza sono costanti
▸ Per b + c < 1 la funzione a ⋅ xb ⋅ yc è omogenea di
grado inferiore ad 1: questo vuol dire che se aumenta di n volte la quantità di
entrambi i beni consumati l’utilità aumenta di meno di n volte.
Il grafico delle curve di indifferenza è allora
il seguente:
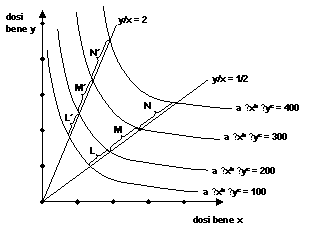
(le linee y/x = ½ e y/x = 2 sono linee lungo le quali è costante
il rapporto tra la quantità di x e la quantità di y consumata)
Come si vede, le distanze L, M, N (L’, M’, N’) tra successive
curve di indifferenza sono crescenti
▸ Per b + c > 1 la funzione a ⋅ xb ⋅ yc è omogenea di
grado superiore ad 1: questo vuol dire che se aumenta di n volte la quantità di
entrambi i beni consumati l’utilità aumenta di più di n volte. Il grafico delle
curve di indifferenza è allora il seguente:
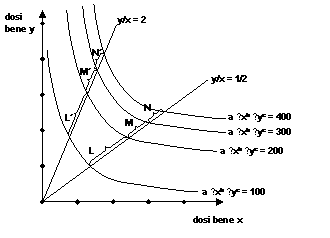
(le linee y/x = ½ e y/x = 2 sono linee lungo le quali è costante
il rapporto tra la quantità di x e la quantità di y consumata)
Come si vede, le distanze L, M, N (L’, M’, N’) tra successive
curve di indifferenza sono decrescenti
Ovviamente, data la ipotesi sulle utilità marginali decrescenti
del consumatore, le curva di livello più realistiche sono quelle in cui la
funzione è omogenea di grado inferiore ad 1.
❍ IL SIGNIFICATO DELLA PENDENZA DELLA CURVA DI
INDIFFERENZA
Qual è il significato della pendenza della curva di indifferenza?

Osservando la figura 027 notiamo che la pendenza P è pari a:
![]()
dove Δc è una variazione della quantità di carne nel
paniere che fornisce UT = 100, e Δv è la quantità di verdura la
cui utilità è pari a quella di Δc.
Possiamo quindi scrivere:
Δc ⋅ UMAcarne = Δv ⋅ UMAverdura
e quindi si ha:
![]()
e quindi:
![]()
Poiché il rapporto ![]() ci fornisce
la quantità di verdura in cambio della quale il consumatore rinuncia al consumo
di una unità di carne, P è anche chiamata saggio
marginale di sostituzione della carne con la verdura , indicato con SMSCV.
ci fornisce
la quantità di verdura in cambio della quale il consumatore rinuncia al consumo
di una unità di carne, P è anche chiamata saggio
marginale di sostituzione della carne con la verdura , indicato con SMSCV.
❍ TRACCIAMO LA CURVA DI INDIFFERENZA DEL
CARNIVORO INTOLLERANTE, DEL VEGETARIANO INTOLLERANTE, DEL CARNIVORO TOLLERANTE,
DEL VEGETARIANO TOLLERANTE
Per verificare la propria comprensione, l’alunno dovrebbe provare
a tracciare la curva dei seguenti soggetti:
Carnivoro intollerante (la carne gli apporta una utilità positiva
mentre la verdura gli apporta una utilità negativa):

Vegetariano intollerante (la verdura gli apporta una utilità
positiva, la carne gli apporta una utilità negativa:

Carnivoro tollerante (la carne gli apporta una utilità positiva,
la verdura gli apporta una utiiltà pari a zero):

Vegetariano tollerante (la verdura gli apporta una utilità
positiva, la carne gli apporta una utilità pari a zero):

❍ LA RETTA
DI BILANCIO
La retta di bilancio si definisce come l’insieme dei punti che
rappresentano combinazioni carne-verdura per acquistare le quali il consumatore
sopporta la stessa spesa complessiva.
Per tracciare la retta di bilancio dobbiamo associare ad ogni
punto una data spesa. Supponendo che il prezzo di una dose di carne sia di 2 €
e che il prezzo di una dose di verdura sia di 1 €, in figura 016 è mostrata la
spesa complessiva associata ad alcuni punti:
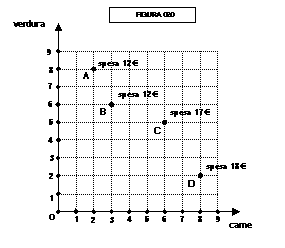
Scegliamo ora, nella figura 017, un punto a caso: il punto A
rappresenta una combinazione di 9 dosi di carne e 2 dosi di verdura, per
acquistare la quale il consumatore spende 13 €.
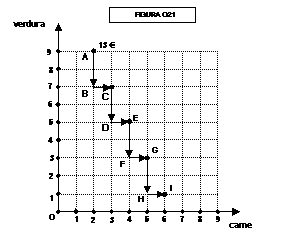
Se ora ci spostiamo in basso, rinunciando a due unità di verdura
(punto B) la spesa sarà diminuita (11 €). Se aumentiamo di una unità il consumo
di carne, ci spostiamo nuovamente verso destra (punto C) e la spesa ritorna ad
essere di 13 €: in pratica non abbiamo fatto altro che sostituire, nel nostro
paniere, due unità di verdura con una unità di carne, lasciando invariata la
spesa totale. Proseguendo secondo questo metodo si incontrano successivamente i
punti A, B, C, D, E, F, G, H e si trova che i punti A, C, E, G sono
caratterizzati da una spesa di 13 €, mentre i punti B, D, F, H sono
caratterizzati da una spesa di 11 €.
Unendo queste due serie di punti otteniamo, nella figura 018, due
diverse rette di bilancio:

❍ IL SIGNIFICATO DELLA PENDENZA DELLA RETTA DI
BILANCIO

Osservando la figura 023 si nota come la pendenza della retta di
bilancio è pari a:
![]()
dove Δc è una variazione della quantità di carne nel
paniere acquistabile con 20 € mentre Δv è la quantità di verdura che
si può acquistare con la stessa somma con cui si può acquistare Δc
Perciò si ha:
![]()
da cui:
![]()
e quindi:
![]()
Vediamo così che la pendenza della retta di bilancio è pari al
prezzo relativo della carne rispetto alla verdura.
❍ IL SIGNIFICATO DEGLI SPOSTAMENTI DELLA RETTA DI
BILANCIO
Supponiamo di partire da una situazione in cui il prezzo di una
dose di carne sia di 2 €, quello di una dose di verdura sia di 1 € e che il
reddito a disposizione del consumatore sia di 8 €.
La retta di bilancio avrà l’andamento AB mostrato dalla figura
023:
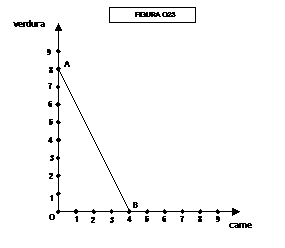
Il punto di intersezione con l’asse verticale rappresenta il caso
di consumo di sola verdura (0 dosi di carne e 8 dosi di verdura), mentre il
punto di intersezione con l’asse orizzontale rappresenta il caso di consumo di
sola carne (4 dosi di carne e 0 dosi di verdura).
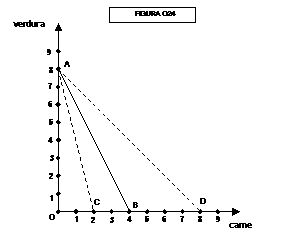
Se ora facciamo raddoppiare il prezzo della carne, la curva subirà
lo spostamento da AB ad AC in figura 020 mentre se facciamo dimezzare il prezzo
della carne la curva subirà lo spostamento da AB a AD
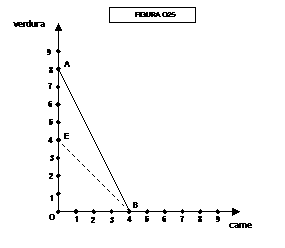
Se invece facciamo raddoppiare il prezzo della verdura la curva
subirà lo spostamento da AB a EB in figura 025:
Se facciamo raddoppiare il reddito del soggetto, la retta di
bilancio si sposterà parallelamente a se stessa verso destra, passando da AB a
CD, mentre se il reddito dimezza la retta si sposterà parallelamente a se
stessa verso sinistra, da AB a EF:
❍ LA COMBINAZIONE DELLA RETTA DI BILANCIO CON LA
CURVA DI INDIFFERENZA
Tracciamo ora insieme, nello stesso grafico (figura 026), la retta
di bilancio e la curva di indifferenza:

I punti sulla retta di bilancio rappresentano la spesa massima che
il consumatore può fare; i punti a destra della retta di bilancio rappresentano
combinazioni che il consumatore non ha soldi per acquistare; i punti a sinistra
della retta di bilancio (area OAB, escludendo i punti sulla retta)
rappresentano le combinazioni acquistando le quali il consumatore non spende
tutti i suoi soldi.
Supponiamo che il nostro consumatore desideri spendere tutti i
suoi soldi: egli si muoverà quindi esclusivamente sulla retta di bilancio, e
dovrà decidere quale punto di tale retta scegliere.
Il consumatore sceglierà il punto P, che gli fornisce la massima
utilità totale. Non può scegliere il punto S (che gli fornirebbe una utilità di
300) perché la combinazione costa più di quanto egli disponga; non sceglierà le
combinazioni Q o R perché esse gli forniscono solo una utilità di 100 mentre P
gli fornisce una utilità di 200.
❍ UNA DIMOSTRAZIONE ALTERNATIVA DELLA LEGGE
DELL’UGUAGLIANZA DELLE UTILITA’ MARGINALI PONDERATE, CHE UTILIZZA LA CURVA DI
INDIFFERENZA E LA RETTA DI BILANCIO
Consideriamo il punto di tangenza della curva di indifferenza con
la retta di bilancio (figura 029) che sappiamo essere il punto di massima
utilità totale:

Se dal punto P ci spostiamo a destra di una quantità Δc (segmento AB) avremo
sull’asse verticale spostamenti diversi a seconda che prendiamo in
considerazione la retta di bilancio (Δv = EC) o la curva di indifferenza (Δv’ = DC)
Avremo perciò:
Δv ≠ Δv’
Ma se riduciamo Δc, la
differenza tra i Δv e Δv’ diviene sempre più
trascurabile. In altre parole, per valori molto piccoli (“infinitesimali”) di Δc possiamo considerare esatta
l’eguaglianza:
Δv = Δv’
e quindi esatta l’eguaglianza:
![]()
e quindi esatta l’eguaglianza:
![]()
dalla eguaglianza sopra indicata, con semplici passaggi algebrici,
si ricava:
![]()
da cui si ricava ancora:
![]()
che equivale a:
UMAPcarne = UMAPverdura
che è la legge che avevamo già trovato graficamente (legge
dell’eguaglianza delle utilità marginali ponderate)
❍ ESEMPI DI
ANDAMENTO ANOMALO DELLA CURVA DI DOMANDA DOVUTI ALL'EFFETTO DI REDDITO
Una famiglia molto povera è costretta a destinare tutte le sue
spese alimentari all'acquisto di fagioli anziché di carne. Infatti, il suo reddito
è talmente basso che la quantità di carne acquistabile è insufficiente per le
necessità dell'organismo. Se il prezzo dei fagioli diminuisce in modo
consistente la famiglia preferirà acquistare la stessa quantità di fagioli o
una quantità inferiore e un po' di carne.
Supponiamo invece che una famiglia utilizzi olio di semi per
friggere e olio di oliva per condire l'insalata. Se il prezzo dell'olio di semi
aumenta la famiglia troverà che, per le sue fritture, deve ora spendere una
cifra che non gli consente più di acquistare olio d'oliva. Perciò deciderà di
usare l'olio di semi anche per l'insalata, e il consumo di olio di semi
aumenterà.
Supponiamo invece che una famiglia sia troppo povera per usare
l'olio di oliva ed usi al suo posto l'olio di semi. Se il prezzo dell'olio di
semi diminuisce in misura rilevante, la famiglia potrà acquitare l'olio di
oliva e il consumo di olio di semi pertanto diminuirà.
Infine consideraimo la curva di domanda di tempo libero di un
lavoratore. Normalmente, se il salario orario aumenta, diminuisce la domanda di
tempo libero. Tuttavia, se il lavoratore riceveva un salario orario molto basso
che lo costringeva a lavorare tute le ore lavorabili al solo scopo di
sopravvivere, un aumento modesto di salario non lo convincerò a lavorare di
più, ma piuttosto a lavorare di meno: ottenuto il salario di sopravvivenza,
egli preferirà passare le ore successive fuori della fabbrica a chiacchierare
con gli amici piuttosto che trascorrerle al lavoro e ottnenere delle somme che
gli consentirebbero di acquistare poco o nulla di più.
❍ L’EFFETTO DI UNA DIMINUZIONE DEL PREZZO DI UN
BENE SUL SUO CONSUMO. L’EFFETTO DI REDDITO E L’EFFETTO DI SOSTITUZIONE
Osserviamo il grafico di figura 030:

La situazione originaria è quella illustrata dalla retta di
bilancio AB e il punto di massima utilità totale è L.
Se facciamo diminuire il prezzo della carne la nuova retta di
bilancio sarà AC e il punto di massima utilità totale è I.
Come si può vedere, la quantità di carne acquistata aumenta,
passando da OF a OH. In altre parole, la curva di indifferenza e la retta di
bilancio mostrano che una diminuzione di
prezzo provoca un aumento del consumo del bene il cui prezzo è diminuito : infatti il consumo di carne passa da OF ad OH
L’utilità totale del soggetto passa da 100 a 200
Solitamente gli economisti spezzano lo spostamento da FH (da OF ad
OH) in due spostamenti parziali:

Come si vede dalla figura 031, gli economisti fanno arretrare la
linea AC parallelamente a se stessa fino alla posizione ED: questo equivale a
far diminuire il reddito del consumatore fino al punto in cui egli non si può
permettere combinazioni di utilità superiore a 100. Si nota che, pur non
aumentando la propria utilità, il consumatore ha cambiato però la propria
scelta dal punto L al punto M.
In altre parole: se consentiamo al consumatore di muoversi lungo
la vecchia curva di indiffernza alla ricerca di una combinazione più economica
avremo uno spostamento che è un effetto di sostituzione.
E’ come se in un primo momento il consumatore, essendo diminuito
il prezzo della carne, si preoccupa solo di avere l’utilità che aveva in
precedenza ad un prezzo più basso (effetto di sostituzione). Successivamente
egli scopre di avere ancora soldi da
spendere; aumenterà quindi sia gli acquisti di carne che di verdura (effetto di
reddito).
Lo spostamento FG, dal punto L al punto M, è chiamato “effetto di
sostituzione”.
Successivamente gli studiosi fanno spostare la retta di bilancio
da ED ad AC (equivalente ad un aumento di reddito del consumatore) e la nuova
scelta è I.
Lo spostamento GH, dal punto M al punto I, è chiamato “effetto di
reddito”.
Ci sono importanti differenze tra l’effetto di reddito e l’effetto
di sostituzione:
l’effetto di sostituzione non può mai essere
negativo (cioè non può mai condurre ad una diminuzione del consumo del bene il
cui prezzo è diminuito), mentre l’effetto di reddito può essere sia positivo
(aumento del consumo del bene il cui prezzo è diminuito) o negativo (diminuzione
del consumo del bene il cui prezzo è diminuito).
Da questo deriva che:
Se l’effetto di reddito è negativo ed è
superiore all’effetto di sostituzione, allora, contro tutte le aspettative, il
consumo del bene il cui prezzo è aumentato aumenterà (ovvero il consumo del
bene il cui prezzo è diminuito diminuirà)
L’effetto di reddito sarà negativo (aumento del
consumo del bene il cui prezzo è diminuito) nel caso di beni inferiori (cioè di
beni, come le patate, la carne scadente ecc.) il cui consumo normalmente
diminuisce all’aumentare del reddito del consumatore)
Per capire quest’ultima affermazione, leggiamo il paragrafo
successivo, che analizza un caso del genere, storicamente verificatosi in
Irlanda nella metà dell’800.
❍ EFFETTO DI REDDITO NEGATIVO: IL FAMOSO CASO
DELLE PATATE IRLANDESI
Come si è già detto, quello che stiamo per analizzare è un caso
realmente verificatosi nell’Irlanda dell’800, dove una carestia provocò
l’aumento del prezzo delle patate, ma si osservò che il consumo di queste
aumentò. Il primo ad osservare il fenomeno e a proporne una spiegazione fu
l’ingegnere mineriario Giffen, e da allora, per indicare beni il cui consumo
aumenta all’aumentare del prezzo si parla di beni di Giffen.
Supponiamo che la situazione di una famiglia irlandese prima
dell’aumento del prezzo delle patate sia la seguente:
Reddito giornaliero 2,756
€
Calorie di un grammo di patate 0,8
Calorie per grammo di carne 1,2
Prezzo di 1 kg di patate 1 €
Prezzo di 1 kg di carne 10 €
Calorie minime giornaliere per
sopravvivenza 1100
Consumo giornaliero di carne
(calorie) 195
Consumo giornaliero di patata
(calorie) 905
Spesa giornaliera per carne 1,625 €
Spesa giornaliera per patate 1,131 €
Vediamo ora come cambia la situazione dopo la carestia, quando il
prezzo delle patate passa a 2 €:
Reddito giornaliero 2,756 €
Calorie di un grammo di patate 0,8
Calorie per grammo di carne 1,2
Prezzo di 1 kg di patate 2 €
Prezzo di 1 kg di carne 10 €
Calorie minime giornaliere per
sopravvivenza 1100
Consumo giornaliero di carne
(calorie) 0
Consumo giornaliero di patata
(calorie) 1100
Spesa giornaliera per carne 0 €
Spesa giornaliera per patate 2,756 €
Cosa è accaduto? E’ accaduto che le patate sono divenute talmente
costose che se la famiglia consumasse anche solo un grammo di carne non
riuscirebbe ad ottenere le calorie quotidiane sufficienti per vivere. Essa
quindi deve passare alle patate, e la domanda di patate aumenterà.
In altre parole: le patate sono beni inferiori, il cui consumo
normalmente diminuisce all’aumentare del reddito. La carestia ha fatto
aumentare il prezzo delle patate e questo ha avuto lo stesso effetto di una
diminuzione di reddito delle famiglie. Ma con l’impoverimento delle famiglie
torna ad aumentare il consumo di patate.
❍ I FATTORI CHE INFLUENZANO LA DOMANDA DI UN BENE: IL PREZZO DEL BENE. LA
CURVA DI DOMANDA DEL BENE
In base a quanto abbiamo visto con le curve di indifferenza nel
caso dell’aumento del prezzo di un bene, possiamo concludere che normalmente (a
parte il caso di beni inferiori) all’aumentare del prezzo di un bene la
quantità domandata diminuisce. Si tratta della cosiddetta curva di domanda di
un bene:

Oltre che con la retta di bilancio e la curva di indifferenza, è
possibile dimostrare in altri modi che la curva di domanda di un bene è
discendente verso destra (esprime cioè un rapporto inverso tra prezzo e
domanda). Supponiamo che esistano solo due beni, carne e verdura; come sappiamo,
il consumatore ne consumerà quantità tali da eguagliare le utilità dell’ultimo
cent (= centesimo di euro) speso in carne con quella dell’ultimo cent speso in
verdura (infatti, se l’utilità dell’ultimo cent speso in carne fosse maggiore
di quella dell’ultimo cent speso in verdura egli potrebbe sempre aumentare la
utiltà totale acquistando un cent di carne in più e un cent di verdura in
meno). Cosa potrà invogliare il consumatore ad aumentare il consumo di verdura?
Egli non consumerà la dose successiva di verdura, perché la sua utilità
marginale è più bassa di quella dell’ultima dose consumata e fornirebbe una
utilità per cent inferiore a quella che fornirebbe la carne. Occorre quindi
aumentare la utilità per cent della successiva dose di verdura. Questo può essere
fatto solo diminuendo il prezzo della verdura. In conseguenza della diminuzione
di prezzo della verdura, l’utilità per cent della successiva dose non consumata
di verdura diverrà superiore a quella della carne, e il consumatore aumenterà
il consumo della verdura, per l’effetto di sostituzione.
❍ L’ELASTICITA’ DELLA DOMANDA RISPETTO AL PREZZO
Per elasticità finita della domanda rispetto al prezzo nell’arco
PQ si intende il rapporto tra la variazione percentuale della domanda e la
variazione percentuale del prezzo, espresso dalla formula seguente:
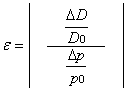
che si riferisce al grafico della curva di domanda del
consumatore:
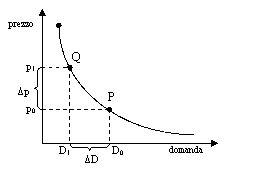
per elasticità puntuale della domanda rispetto al prezzo nel punto
P si intende il rapporto:
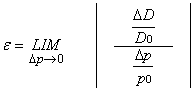
che si legge: “limite, per Δp che tende a zero, della espressione racchiusa
tra i segni di valore assoluto”.
A fini pratici e di immediata visualizzazione, possiamo definire
la elasticità puntuale come il medesimo rapporto:
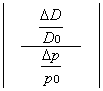
calcolato però in riferimento alla retta tangente r alla curva di
domanda nel punto P, come se essa, e non la curva d fosse la vera curva di
domanda:

❍ ELASTICITA’
ZERO ED ELASTICITA’ INFINITA
Convenzionalmente si definisce “elasticità pari a zero” quella
della figura 042, mentre si definisce “elasticità infinita” quella della figura
043:


❍ SE AUMENTIAMO IL PREZZO DEL BIGLIETTO
DELL’AUTOBUS, I RICAVI DELL’AZIENDA DI TRASPORTI AUMENTERANNO O DIMINUIRANNO?
L’elasticità può essere vista come il rapporto tra la variazione
percentuale della domanda e la variazione percentuale del prezzo:

così, una elasticità ε = 3, supponendo che si tratti della domanda e
del prezzo della carne, indica che, se il prezzo della carne aumenta del 10% la
domanda di carne diminuisce del 30% ( ![]() )
)
Supponendo che l’elasticità della domanda di trasporti mediante
autobus sia pari a 3, per stabilire se i ricavi dell’azienda di trasporto
aumenteranno o diminuiranno a seguito di un aumento di prezzo del 10%,
impostiamo la seguente espressione:
Ricavi totali = p · D
dove p è il prezzo del
biglietto e D è la domanda di
biglietti
Dopo l’aumento del 10% del prezzo questa espressione si trasforma
in:
![]()
che con semplici passaggi algebrici si trasforma in:
![]()
Si vede quindi che a seguito di un aumento di prezzo del 10% i
ricavi diminuiranno del 33%
La
variazione dei ricavi totali a seguito di un aumento (diminuzione) di prezzo
dipende dalla elasticità:
ε = 1 à ΔRT ≃ 0
ε > 1 à ΔRT < 0 (“domanda elastica”)
ε < 1 à ΔRT > 0 (“domanda rigida”)
❍ I FATTORI CHE INFLUENZANO LA DOMANDA DI UN
BENE: IL PREZZO DEI BENI SUCCEDANEI
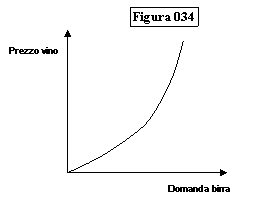
Si dicono beni succedanei due beni che, entro una certa misura,
possono sostituirsi l’uno all’altro nel consumo, come il vino e la birra, il
burro e la margarina, il the o il caffè
Tra la domanda di un bene e il prezzo del suo succedaneo esiste
una relazione diretta:
❍ I FATTORI CHE INFLUENZANO LA DOMANDA: I PREZZI
DEI BENI COMPLEMENTARI
Definiamo beni complementari due beni se non è possibile consumare
l’uno senza l’altro (es. auto e benzina) o se uno di essi, consumato insieme
all’altro, fornisce una utilità superiore al consumo separato (es. caffè e
zucchero)
Tra la domanda di un bene e il prezzo del suo complementare esiste
un rapporto inverso:
![]()
![]()

❍ I FATTORI CHE INFLUENZANO LA DOMANDA: IL
REDDITO DEL CONSUMATORE
Se misuriamo la domanda di un bene in funzione del reddito del
consumatore, si presentano 4 casi.
Primo caso (beni inferiori tipo sale):
![]()
![]()
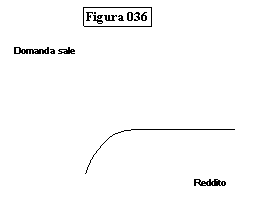
Secondo caso (beni inferiori tipo patate):
![]()
![]()

Terzo caso (beni normali):
![]()
![]()

Per beni normali la domanda di solito aumenta meno che
proporzionalmente all’aumentare del reddito
Quarto caso (beni di lusso):
![]()
![]()

❍ ALTRI FATTORI CHE INFLUISCONO SULLA DOMANDA DI
UN BENE
Tra gli altri fattori che possono influire sulla domanda di un
bene ricordiamo:
● La distribuzione della ricchezza tra le
famiglie può influenzare il tipo di consumi dell’intera nazione. Un emirato
arabo in cui lo sceicco abbia il 99% del reddito e il resto della popolazione
solo l’1% probabilmente consumerà beni di lusso più dello stesso emirato dopo
che una rivolta proletaria abbia espropriato lo sceicco e distribuito le sue
ricchezze ai poveri
● Età del consumatore. Gli economisti hanno ad
esempio mostrato che le persone giovani consumano meno di quanto ricavano come
reddito, mentre le persone anziane consumano più di quanto ricavano come
reddito
● Periodo dell’anno
● Sesso
● Gusti del consumatore
● Livello di istruzione e di informazione
❍ LA CLAUSOLA “CETERIS PARIBUS”
Ogni volta che un economista vuole studiare la dipendenza della
domanda da un particolare fattore (prezzo del bene, prezzi degli altri beni
ecc.) egli si trova di fronte il problema di isolare gli effetti di uno dei
fattori da quelli degli altri: se il prezzo del bene è aumentato, ma quello del
suo succedaneo è diminuito, come si può sapere quanta parte dell’aumento di
consumo che ne consegue sia dovuta ad una variazione del prezzo del bene e
quanta parte ad una variazione del prezzo del succedaneo?
La situazione ideale dell’economista sarebbe ovviamente che,
quando varia il fattore che si sta studiando (es. il prezzo del bene) non varii
nessun altro fattore (es. il prezzo del bene succedaneo). Questa condizione
ottimale per studiare l’influenza di un solo fattore alla volta prende il nome
di “ceteris paribus”.
Facciamo un esempio per chiarire il concetto. Supponiamo che un
economista sia nascosto nella cantina della vostra abitazione e voglia provare
la seguente ipotesi: se la tariffa dell’acqua diminuisce, il consumo della
famiglia aumenta.
Se l’economista però non si preoccupa di tenere sottocontrollo
tutti gli altri fattori che influenzano il consumo di acqua della vostra
famiglia (gusti, grado di inquinamento ambientale, numero dei componenti della
famiglia, precipitazioni temporalesche, numero di animali posseduti ecc.) egli
otterrà dati falsati.
❍ APPROFONDIAMO LA DIPENDENZA DEL CONSUMO DAL
REDDITO
Tracciamo il grafico dei consumi complessivi di una famiglia in
funzione del reddito:


Tale grafico prende il nome di funzione del consumo. Il rapporto
DC / BC nel primo grafico prende il nome di propensione marginale al consumo ed
è pari a:
![]()
La propensione marginale al consumo può assumere i seguenti
valori:
0 ≤ c ≤ 1
essa rappresenta la percentuale dell’ultima frazione di reddito
che la famiglia destina a consumi
Il grafico di destra è una forma semplificata di quello di
sinistra; la equazione della funzione di consumo semplificata è quella di una
retta:
C = C0 + c · Y
dove c minuscolo è pari
alla propensione media al consumo:
![]()
La propensione media al consumo indica la percentuale del reddito
che la famiglia destina a consumi
di solito, nei testi economici, quando si parla di c si allude alla propensione marginale
Come si vede dalla figura 040, all’aumentare del reddito
diminuisce la propensione marginale al consumo; infatti si ha:
![]()
questo significa che all’aumentare della ricchezza una famiglia
destina una percentuale inferiore del proprio reddito alle spese di consumo e
una percentuale sempre maggiore al risparmio.
Il rapporto che lega la propensione (media o marginale) al consumo
e la propensione (media o marginale) al risparmio (che indicheremo con s) è il seguente:
s = 1 - c
❍ LA RENDITA DEL CONSUMATORE
Osserviamo la figura 044:
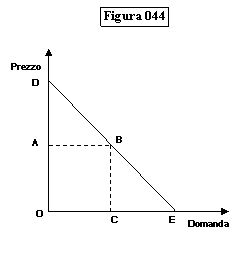
Se il prezzo di mercato è OA, l’area dei ricavi dell’imprenditore
è OABC
L’area ABD è invece chiamata “rendita del consumatore” e
rappresenta somme aggiuntive che i consumatori sarebbero disposti a pagare per
il bene, ma che l’imprenditore, se pratica un prezzo unico, non riesce a farsi pagare.
❍ LO SCAMBIO
Con lo scambio tra due beni ciascuno dei due partecipanti cerca di
aumentare le utilità a sua disposizione.
Si definisce baratto lo scambio in natura (bene contro bene), in
contrapposto allo scambio monetario che non è altro che un baratto spezzato in
due: dapprima Tizio cede il suo libro a Caio e ne ottiene moneta;
successivamente Caio cede la moneta a Sempronio e ne ottiene una penna. E’ come
se un atto di baratto tra Tizio e Sempronio (libro contro penna) sia stato
spezzato in due atti di scambio monetario indipendenti.
Osserviamo il grafico sottostante, chiamato grafico a scatola di
Edgeworth:

Ogni punto nel grafico a scatola rappresenta una spartizione di
pesche e mele tra Mario e Giorgio.
Ad esempio, il punto A rappresenta la seguente spartizione:
3 mele a Giorgio e 6 mele a Mario
4 pesche a Giorgio e 4 pesche a Mario
Il punto B rappresenta la seguente spartizione:
11 mele a Giorgio e 3 mele a Mario
6 pesche a Giorgio e 2 pesche a Mario
Riportiamo ora, nel grafico, le curve di indifferenza di Giorgio e
di Mario:

Se il punto che rappresenta la attuale spartizione di mele e
pesche si trova in una delle aree in cui sia Giorgio che Mario hanno una UT
< 100 (ad es. il punto P nell’area in alto a sinistra) ad entrambi converrà
spostarsi nell’area in cui tutte e due hanno UT > 100 (ad es. il punto Q
nell’area centrale). In tal caso si passerà da P a Q e si sarà realizzato uno
scambio.
❍ LA SCELTA DELLA FAMIGLIA TRA CONSUMO E
RISPARMIO (COME DIVENTARE MILIONARI CON LA PAGHETTA)
Isabella riceve dal padre una paghetta di 3 € al mese. Il padre,
per abituare Isabella a risparmiare, le offre una scelta: le darà un interesse
del 100% che le pagherà il mese successivo sulle somme risparmiate il mese
precedente. Isabella, aiutata dal prof di economia, costruisce il diagramma
riportato sotto:
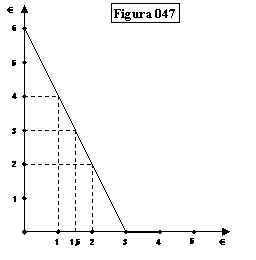
Se leggiamo sull’asse orizzontale la somma spesa da Isabella, il
punto corrispondente sull’asse verticale indica la somma risparmiata più gli
interessi che sono maturati durante il mese: è la somma che il mese successivo
si aggiunge alla paghetta di tale mese.
Si vede così che se Isabella spende a Gennaio 1 € della paghetta
di Gennaio, il mese successivo, oltre la paghetta, avrà da spendere 4 € di
somme risparmiate più interessi; se spende 1,5
€ il mese successivo, oltre la paghetta, avrà da spendere 3 € di somme
risparmiate più interessi; se spende 2 € il mese successivo, oltre la paghetta,
avrà da spendere 2 € di somme risparmiate più interessi; se spende 3 € il mese
successivo avrà solo la paghetta, perché non vi saranno interessi.
Anche una famiglia deve fare la stessa scelta tra consumo e
risparmio.
❍ LA SCELTA DELLA FAMIGLIA CIRCA IL MODO DI
TENERE LA PROPRIA RICCHEZZA. IL PORTAFOGLIO.
Tutti i soggetti della economia (stato, enti pubblici, imprese,
famiglie, banche, ecc.) posseggono un portafoglio.
Il portafoglio è un insieme di attività e passività con diverso
rendimento, rischio e scadenza.
Per "attività patrimoniale" o, semplicemente,
"attività" si intende qualsiasi cosa appartenga ad un soggetto e
costituisca ricchezza.
Il portafoglio di un soggetto può contenere attività che vanno
dalle più liquide (moneta) alle meno liquide:
▸ Moneta
▸ Obbligazioni, altri titoli a reddito fisso e
crediti con scadenza a breve termine
▸ Obbligazioni, altri titoli a reddito fisso e
crediti con scadenza a lungo termine
▸ Azioni
▸ Beni di consumo durevoli
▸ Beni di consumo non durevoli
▸ Beni aziendali (le imprese)
▸ Capitale umano (le abilità e le conoscenze
"spendibili" sul mercato del lavoro)
Il portafoglio può anche contenere passività sotto forma di:
▸ Debiti pecuniari bancari
▸ Debiti pecuniari verso soggetti non bancari
(imprese, famiglie)
In sintesi, si può dire che un portafoglio è composto
principalmente da attività finanziarie: (moneta, obbligazioni e azioni) e
attività reali (macchine, terreni, fabbricati posseduti dalle imprese, beni di
consumo durevoli ,abitazioni possedute dalle famiglie).
A tutte le attività del portafoglio sono ricollegabili rendimenti positivi
o negativi. Le attività reali (cioè quelle che consistono in beni) forniscono
un rendimento che si differenzia da una attività all'altra. Ad es. il
rendimento dei beni di proprietà è pari al valore dei servizi che altrimenti il
soggetto dovrebbe procurarsi pagando (così una casa di abitazione di proprietà
del soggetto ha come rendimento una somma pari al canone di locazione che egli
dovrebbe altrimenti pagare); il rendimento del capitale umano è pari al reddito
che esso può o potrà procurare con l'attività lavorativa; le macchine offrono
alla impresa che le possiede un contirbuto alla produzione e quindi alla
crazione di profitti.
Per "Scelte di portafoglio" si intendono le scelte che
continuamente i soggetti compiono per determinare la composizione del proprio
portafoglio (ad es. scelta tra moneta, titoli a breve, titoli a lungo termine)
in modo da massimizzare i rendimenti di tale portafoglio. Molte di tali scelte
sono estremamente importanti per spiegare variazioni o perturbazioni nella
attività economica. Ad esempio, se tutte le famiglie decidono di diminuire la
quota di ricchezza detenuta sotto forma di moneta e di sostituirla con titoli
si avrà un aumento del valore dei titoli, una diminuzione del saggio di
interesse, un (probabile) aumento degli investimenti e un (probabile)
incremento del reddito nazionale.
Un portafoglio contiene attività più o meno "liquide":
quanto più facilmente una attività che non è moneta può essere convertita in
moneta, tanto più tale attività è liquida. Un esempio di attività liquide sono
i titoli di stato a breve scadenza (i BOT), che possono essere prontamente
venduti e trasformati in moneta o dati in garanzia per ottenere un prestito in
moneta.
❍ LA SCELTA DELLA FAMIGLIA TRA LAVORO E TEMPO
LIBERO
Tre sono gli elementi che il lavoratore considera per decidere la
sua offerta di lavoro:
▸ La penosità del lavoro: la penosità di ciascuna
ora lavoro aumenta all’aumentare del numero di ore lavorate
▸ La utilità ricavabile con i beni acquistabili
col salario
▸ La utilità ricavabile dal tempo libero
L'economista Alfred Marshall studiò l’offerta di lavoro con le
curve di indifferenza:
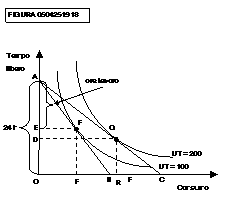
Nella figura 0504251918 si vede come vi sono curve di indifferenza
diverse, che presentano combinazioni lavoro-consumo aventi la stessa utilità
(nell’esempio, UT = 100 o UT = 200). Contemporaneamente, però, dato il salario,
ha il vincolo della linea AB. Il punto P rappresenta il suo equilibrio, e le
ore di lavoro offerte sono pari ad AE.
Se il salario aumenta, il suo vincolo è quello della linea AC e il
suo punto di equilibrio è Q.
Si può vedere che le ore offerte passano da AE ad AD, aumentando.
Ma, come nota Marshall, e come sappiamo dallo studio delle curve
di indifferenza del consumatore, in realtà gli effetti che entrano in gioco con
uno spostamento della retta AB sono due:
▸ Un "effetto di sostituzione", che
spinge il lavoratore alla riduzione del tempo libero e all'aumentare
correlativo del tempo di lavoro
▸ Un "effetto di reddito" che spinge,
viceversa, il lavoratore, alla diminuzione del tempo di lavoro e all'aumento
del tempo libero
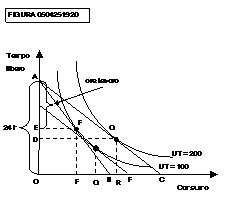
Questi due effetti sono individuati nella figura 0504251920, dove
la variazione PR del consumo, conseguente allo spostamento dal segmento AB al
segmento AC è divisa in due spostamenti: PQ (effetto di sostituzione) e QR
(effetto di reddito).
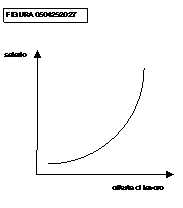
A bassi livelli salariali prevale in genere l'effetto
sostituzione, mentre a livelli salariali più elevati tende a prevalere
l'effetto di reddito, che conduce a preferire il tempo libero al lavoro.
L'andamento dell'offerta di lavoro in funzione del salario è quindi quello di
figura 0504252027
Consideriamo ora un caso molto particolare, in cui il salario è
talmente basso che prevale l’effetto di reddito, e un aumento di salario porta
ad una diminuzione delle ore
lavorate.
Consideriamo l’operaio Cipputi, a cui viene pagato un salario
bassissimo:

Se il minimo di sussistenza giornaliero è di 5 € e il salario è
molto basso (ad es. inferiore a 1 € l’ora Cipputi lavorerà solo il numero di
ore strettamente sufficienti per avere il minimo di sussistenza: con un salario
di 0,25 € l’ora egli lavorerà 20 ore (quante sono necessarie per guadagnare 5
€); con un salario di 0,5 € l’ora egli lavorerà 10 ore; con un salario di 0,75
€ l’ora egli lavorerà 0,66 ore; con un salario di 1 € l’ora egli lavorerà solo
5 ore: infatti il salario è così basso che è più utile il tempo libero che ciò
che si può ricavare dai beni acquistabili col salario.
Solo quando il salario supera 1,25 € l’ora, nel nostro esempio,
Cipputi comincia ad aumentare la sua offerta di ore lavoro.