IL SISTEMA ECONOMICO
❍ Sia l'economia che il diritto studiano il gruppo umano,
ma da due differenti punti di vista
● Sia
che l'economia che il diritto studiano il funzionamento del gruppo umano.
Sia l'economia che il diritto
studiano il gruppo umano, ma da punti di vista differenti.
Il diritto vede il gruppo come
un insieme di persone i cui comportamenti sono regolati da norme di condotta.
Il nome che si dà a tale gruppo è Stato (più raramente: istituzione).
● Il
punto di vista dell'economia.
L'economia vede il gruppo come
un insieme di persone che hanno a disposizione delle risorse limitate (materie
prime, lavoro, ecc.) e le impiegano per produrre beni o servizi con cui
soddisfare i propri bisogni. Il gruppo visto dall'economista si chiama sistema
economico.
❍ Alla base dei comportamenti economici ci sono i bisogni
● Cos'è
un bisogno
Per "bisogno" si
intende una sensazione penosa di insoddisfazione che spinge l'individuo a
cercare i mezzi per eliminarla.
● Bisogni
primari e bisogni secondari
I bisogni primari sono quelli
indispensabili alla sopravvivenza di un individuo
I bisogni secondari o di civiltà
(istruzione,trasporti, televisione, vacanze ecc) sono quelli la cui
soddisfazione migliora la condizione di vita dell’individuo
● Bisogni
individuali, bisogni collettivi, bisogni pubblici
Esistono "bisogni
individuali" e "bisogni collettivi".
Questi ultimi sono avvertiti
non da singoli individui, ma da tutta la collettività, poiché sono importanti
per la sua (ordinata) sopravvivenza: bisogno di tribunali e di giustizia;
bisogno d'ordine garantito da forze di polizia; bisogno di difesa dello stato
da aggressioni militari, ecc.
Si dicono “bisogni pubblici” i
bisogni collettivi soddisfatti dallo Stato o da un altro ente pubblico, in
quanto il loro soddisfacimento è sentito come particolarmente importante per la
collettività
❍ Le "risorse" o "fattori di
produzione" consentono di produrre beni e servizi
● Cosa
sono le risorse
Per "risorse", o
"fattori di produzione" si intende tutto ciò che può essere
utilizzato per produrre beni e servizi che soddisfino bisogni umani.
● La
risorsa o fattore di produzione “lavoro”
Il lavoro è la capacità dell’uomo di
svolgere una attività manuale o intellettuale
● Le
risorse “beni capitali”
Il lavoro va combinato con
degli strumenti (detti "beni capitali" o "beni
strumentali", o semplicemente, "capitale fisico").
Tra i beni capitali includiamo
sia i beni capitali durevoli, che possono essere usati ripetutamente per produrre
(martello, pressa idraulica, autocarro, ecc...), sia i beni strumentali non
durevoli, chiamati anche semilavorati o materie prime, che vengono distrutti
nel ciclo produttivo senza possibilità di riutilizzazione (es.: la plastica
delle bottiglie, il cuoio delle scarpe, i lingotti di ferro utilizzati per
produrre le lamiere).
● La
differenza tra “materie prime” e “risorse naturali”
Alcuni beni strumentali non durevoli
(semilavorati) prendono il nome di “materie prime”.
Si distinguono “materie prime energetiche”
(petrolio, uranio, carbone…) da “materie prime non energetiche” (ferro, gomma,
legno…)
Le materie prime non sono altro che dei
semilavorati che possiedono le seguenti proprietà:
· Hanno subito
un grado modesto di lavorazione, che le avvicina alle risorse naturali
(con cui però non vanno confuse)
· Sono utilizzabili per un gran numero di
produzioni diverse (si pensi al petrolio, da cui si ricavano combustibili,
fibre tessili, oggetti in plastica ecc)
● La
risorsa "natura" o "risorse naturali"
Accanto alle materie prime
esistono delle risorse prelevate direttamente dalla natura, senza nessuna
trasformazione umana. Il mare, le foreste, i batteri utilizzati nella
fermentazione della birra, sono tutti esempi di ciò che viene chiamato
"risorse naturali" o "natura", a disposizione dell'uomo
senza aver subito nessuna trasformazione precedente.
● Le
conoscenze tecnologiche
Oltre a quelle che abbiamo
elencato occorre un'altra risorsa: le conoscenze tecnologiche. Nessuno infatti
produce il formaggio, pur avendo a disposizione latte e recipienti, se non
conosce il giusto procedimento.
❍ I beni economici. I servizi. La
utilita’
● Cosa
intende l'economista per "bene"?
Per l'economista
"bene" è qualsiasi oggetto che sia in grado di soddisfare,
direttamente (se consumato) o indirettamente (se impiegato nel processo
produttivo), un bisogno.
● Il
bene deve essere utile
La caratteristica principale
del "bene" è l'utilità. Si definisce utile un bene che è in grado di
soddisfare direttamente o indirettamente un bisogno umano.
● La
produzione dei beni
Alcuni beni utili si trovano
già in natura, ma la maggior parte è il prodotto finale di un "processo
produttivo" compiuto dall'uomo mediante la combinazione delle risorse.
● I
"beni economici" sono un sottoinsieme dei "beni".
Gli economisti si occupano più
spesso di quei beni che hanno una utilità nota, sono accessibili, sono presenti
in quantità scarsa e non si occupano che marginalmente di oggetti che non
abbiano queste caratteristiche.
● I
"beni liberi" differiscono dai "beni economici"
L'aria, l'acqua del mare, le
foreste, il sole, sono disponibili in quantità illimitata, e nessuno paga un
prezzo per il loro utilizzo. Essi sono chiamati "beni liberi". Oggi
gli economisti cominciano ad occuparsi dei beni liberi, poiché anche essi
iniziano a diventare scarsi, ed è molto sentita l'esigenza di coordinarne l'uso
tra i vari soggetti (stati, imprese, famiglie) per conservarli e sfruttarli
razionalmente.
● Anche
le "risorse" materiali (natura, materie prime, macchinari, ecc.)
rientrano nella categoria dei "beni".
● Anche
le conoscenze tecnologiche sono considerate particolari tipi di beni
("beni immateriali")
● I
"servizi"
Per "servizi" si
intendono le modificazioni utili che una cosa o l’attività di una persona
apporta ad un altro individuo per soddisfare i suoi bisogni, aumentando le
utilità a sua disposizione. Si dice che mentre il bene è materiale, il servizio
è immateriale. Il taglio dei capelli, la lezione di un professore, il trasporto
da parte di un taxista sono tutti esempi di servizi, considerati
dall'economista allo stesso modo dei beni.
❍ La classificazione dei beni e dei servizi: Strumentali,
di consumo, durevoli, non durevoli
● Beni
e servizi di consumo e beni e servizi strumentali
Sia i beni che i servizi
possono essere suddivisi in due grandi categorie: a) beni o servizi di consumo;
b) beni o servizi strumentali o di produzione. I primi possono essere impiegati
direttamente per soddisfare un bisogno umano (ciclomotori, televisori,
giornali, ecc.); i secondi possono essere utilizzati per produrre beni o
servizi del primo tipo (autocarri, lingotti di ferro, servizi di vigilanza a
negozi e a fabbriche, assicurazione per imprenditori, ecc.). I beni
strumentali, anziché dai consumatori finali, sono utilizzati dai produttori
(imprese).
● Beni
durevoli e non durevoli
Sia i beni (o servizi) di
consumo, sia i beni (o servizi) strumentali possono essere durevoli (=
utilizzabili ripetutamente per più atti di produzione o di consumo) e non
durevoli (= utilizzabili per un solo atto di produzione o di consumo).
● I
beni immateriali
I beni incorporei come le
invenzioni, le creazioni artistiche ecc. sono anche definiti “beni immateriali”
(i servizi, anche se immateriali non sono inclusi tra ciò che si definisce
“beni immateriali”).
● Riepilogo
della classificazione dei beni e servizi
· Beni
· Beni liberi
· Beni economici
· Beni immateriali (invenzioni, creazioni
artistiche ecc.)
· Risorse naturali
· Beni di consumo
· Beni di consumo durevoli (automobili,
televisori ecc.)
· Beni di consumo non durevoli (giornali,
generi alimentari, benzina, sigarette, ecc.)
· Beni strumentali
· Beni strumentali durevoli (autocarri, torni,
martelli ecc.)
· Beni strumentali non durevoli (lingotti di
ferro, pelli, viti ecc.)
· Materie prime
· Altri beni strumentali non durevoli diversi
dalle materie prime
· Servizi
· Servizi di consumo (resi ai consumatori)
(taxi, taglio dei capelli)
· Servizi strumentali (resi alle imprese)
(servizi bancari, di vigilanza)
❍ La classificazione dei beni e servizi: Intermedi e finali
Un'altra distinzione è quella
tra "beni finali" e "beni intermedi". Sono "beni
finali" quelli che nel periodo considerato rappresentano il punto finale
del processo produttivo, in quanto non saranno ulteriormente trasformati (es.
autocarri o presse, che nell'anno di produzione si considerano non ancora
impiegati per produrre altri beni), mentre sono "beni intermedi"
quelli che nel periodo considerato verranno ulteriormente trasformati per ottenere
il bene finale (ad esempio la gomma utilizzata per la costruzione di un
pneumatico è da considerare bene intermedio, perché il processo produttivo
prosegue, trasformandola nel bene finale pneumatico).
Sono chiamate merci i beni che
vengono venduti e acquistati in un mercato; in altre parole che hanno un prezzo
e si possono vendere e comperare. Normalmente tutti i beni economici sono da
considerare merci.
Un altro termine utilizzato per
indicare gli oggetti materiali prodotti con impiego di lavoro umano è quello di
"manufatti".
● Il
concetto di "scarsità" è collegato ai bisogni.
In tutti i sistemi economici
osservabili le risorse disponibili (lavoro, beni strumentali, natura,
conoscenze tecnologiche) non sono sufficienti per soddisfare tutti i bisogni.
Questa situazione viene definita "situazione di scarsità delle
risorse".
Per "risorse scarse"
si intende "scarse rispetto ai bisogni da soddifare". Malgrado l'uomo
sia riuscito ad aumentare la quantità di beni prodotti dall'inizio della sua
storia ad oggi, rimangono ancora molti bisogni insoddisfatti, ed inoltre sono
nati bisogni nuovi, cosicché si può dire che, anche se il numero di beni di cui
possiamo disporre è aumentato a dismisura rispetto ad altri periodi storici,
viviamo ancora in una situazione di scarsità di risorse.
● La
scarsità delle risorse richiede che il sistema economico prenda delle decisioni
Già quanto detto mostra che
l'utilizzo delle risorse per soddisfare i bisogni del gruppo richiede che
vengano prese delle decisioni; poiché non si può soddisfare i bisogni di tutti
né produrre tutto quel che si vuole occorrerà stabilire:
· Cosa produrre
Poiché le risorse sono scarse,
occorre decidere quali beni o servizi produrvi, rinunciando a beni e servizi
meno utili. Domande del tipo: "dovremmo utilizzare il ferro per produrre
mezzi militari o balconi per abitazioni?"; "impiegheremo più terreni
come campi da gioco che come aree fabbricabili o viceversa?" costituiscono
il problema definito "problema di allocazione delle risorse"
consistente appunto del determinare l'uso da fare di risorse scarse.
· In quale misura distribuire ai singoli il
prodotto ottenuto
Stabilire il reddito monetario,
e cioè la somma guadagnata da un individuo che ha preso parte al processo di
produzione, vuol dire attribuirgli una frazione più o meno grande di quel
prodotto.
Domande come: "dovranno
essere più alti i redditi dei camionisti o degli avvocati?" "Chi
stabilisce la parte dei ricavi che va all'imprenditore come profitto e la parte
destinata ai salari?" costituiscono appunto quello che in economia si
chiama "il problema della distribuzione" (delle risorse)
● Un
sistema economico, più che come una macchina per produrre, viene visto
dall'economista come una macchina per prendere decisioni.
Il sistema economico può essere
visto come una grande macchina per prendere queste ed altre importanti
decisioni.
Un sistema economico è quindi
anche e principalmente un sistema che prende decisioni e in cui circolano
informazioni.
● Il
sistema dei prezzi serve a scambiare informazioni tra i soggetti nei sistemi
economici in cui le decisioni vengono prese con il contributo di un gran numero
di individui
In un sistema economico
capitalistico, tutti contribuiscono, col loro comportamento, a formare queste
decisioni: ad esempio le famiglie, domandando una maggiore quantità di un
determinato bene rispetto ad altri ne fa crescere i prezzi, e questo segnala
agli imprenditori quali sono le produzioni più richieste.
A loro volta gli imprenditori
devono fare i conti con il costo delle materie prime e degli altri fattori
produttivi, cercando di economizzare le risorse più scarse (più costose) e di
impegare invece quelle più abbondanti (meno costose).
Un alto prezzo di vendita della
merce da parte dell'imprenditore segnalerà ai consumatori che tale sostituzione
non è pienamente riuscita, e che per la produzione del bene vengono impiegate
risorse scarse, che occorre economizzare.
❍ Allocazione pubblica e allocazione privata delle risorse
Anche lo stato contribuisce a
indirizzare l'attività produttiva, privando, i cittadini ,con il prelievo
fiscale, del potere di spendere una parte dei loro redditi come essi
vorrebbero, e producendo con le somme prelevate beni e servizi che ritiene
(maggiormente) utili per la collettività.
Quando a decidere i beni da
produrre sono i singoli attraverso la loro spesa si parla di "allocazione
privata delle risorse"; quando invece è lo stato a stabilire cosa produrre
attraverso il prelievo fiscale si parla di "allocazione pubblica delle
risorse".
In entrambi i casi si può dire
che sono sempre i singoli membri del sistema a "votare" quali beni
produrre: nella allocazione privata attraverso ogni lira spesa per questo
anziché per quel bene ("una lira - un voto", potremmo dire); nella
allocazione pubblica attraverso la elezione dei propri rappresentanti al
Parlamento ("una testa - un voto", potremmo dire).
Poiché le risorse sono scarse è
interesse di tutti utilizzarle nel modo migliore possibile. L'economista studia
il comportamento dell'individuo che, consapevole della necessità di non
sprecare risorse, cercherà sempre di ottenere la massima utilità da quanto ha a
disposizione. Dovrà quindi agire razionalmente: la persona razionale, che ha
come scopo la massimizzazione della utilità che può ricavare dalle risorse
viene chiamata "homo oeconomicus".
All'"homo
oeconomicus" si contrappone lo "sciocco" o "soggetto non
razionale". L'"homo oeconomicus", essendo un individuo
razionale, posto di fronte ad una scelta, reagirà in modo prevedibile, qualora
se ne conoscano gli obiettivi.
Una persona razionale, di
fronte a due bancarelle che espongono la stessa merce a prezzi diversi
sceglierà quella dal prezzo più basso, perché il suo obiettivo è tipicamente di
massimizzare la propria utilità.
Mentre è possibile creare una
teoria che preveda il comportamento razionale dell'"homo
oeconomicus", il comportamento dello sciocco è difficilmente prevedibile.
Su di lui, sulle sue
motivazioni e le sue strategie gli economisti non possono fare previsioni e
quindi non possono costruire una scienza del suo comportamento che permetta
descriverne i meccanismi e di prevederlo.
Nell'esempio fatto sopra, lo
sciocco potrebbe scegliere la bancarella col prodotto più costoso, ma venduto
dalla fruttivendola con la scollatura.
Una famiglia razionale, per
fare ancora un esempio, se dispone di sole 10.000 lire cercherà di acquistare
con le prime mille lire una dose del bene per essa più utile e cointinuerà
scegliendo via via cosa acquistare tra i beni rimasti più utili.
● I
soggetti economici
Famiglie, imprese, stato ed
enti pubblici (comuni, regioni, IRI, ENI, ecc.), resto del mondo (cioè
famiglie, imprese e autorità del resto del mondo) sono i soggetti economici.
● Le
"famiglie"
Per "famiglia" si
intende più precisamente la unità di consumo: una persona o un gruppo che
prendono unitariamente le decisioni di consumo: cosa consumare.
Un soggetto che vive solo è una
famiglia, come pure un convento, una nave straniera che approda in un porto
italiano e il cui capitano fa acquisti per la navigazione.
● Le
"imprese"
Impresa è la unità di
produzione: una persona o un gruppo di persone (soci) che produce beni o
servizi prendendo decisioni del tipo: quanto produrre, cosa produrre, come
produrre. L'economista considera "impresa" sia un colosso come la
General Motors che l'hippie che fabbrica collanine all'angolo della strada, sia
il piccolo negoziante che vende generi alimentari.
● Il
"resto del mondo"
Come già detto, si tratta delle
imprese, delle autorità e delle famiglie estere
● Soggetti
diversi svolgono attività (parzialmente) diverse.
Il ruolo dei soggetti che
operano nel sistema è quindi diverso. Famiglie, imprese e Stato risparmiano. Le
famiglie consumano. Le imprese e lo stato producono. Le imprese e lo stato
investono. Imprese, famiglie e stato scambiano.
● I
soggetti economici svolgono un certo numero di attività:
· Il consumo
· Lo scambio
· La distribuzione del prodotto alle varie
famiglie
· La produzione
● La
produzione
L'economista definisce
produzione qualsiasi modificazione o trasformazione che aumenti la utilità di
ciò che è a disposizione dei soggetti.
Si distinguono vari tipi di
trasformazione:
· Trasformazione materiale
Ad es. un lingotto di metallo
viene fuso per creare un gioiello; lamiere e altri componenti vengono prodotti
e assemblati per ottenere un'automobile
· Trasformazione nel tempo
Tutte le operazioni di
magazzinaggio, conservazione in celle frigorifere, inscatolamento,
essiccazione, salatura, liofilizzazione, permettono ad un prodotto deperibile
di essere consumato in un momento successivo (formaggi, insaccati, frutta secca
ecc.)
· Trasformazione nello spazio
Tutte le operazioni di
trasporto modificano la posizione dei beni nello spazio
· Trasformazione nel modo
Tutte le operazioni svolte dai
commercianti che acquistano merce sfusa dal grossista, la mettono a
disposizione in piccole porzioni o in esemplari singoli vicino alla abitazione
dei clienti, offrono servizi di consulenza, possono essere considerate
"trasformazioni nel modo"
● Il
risparmio
Gli economisti definiscono
risparmio l'atto con cui un soggetto economico che dispone di un reddito
rinuncia a consumare il suo reddito cioè non lo utilizza per effettuare
consumi.
● L'investimento
E' l'atto con cui le imprese
chiedono/acquistano nuovi beni strumentali durevoli per aumentare il numero di
quelli già posseduti, oppure chiedono/acquistano nuovi beni strumentali non
durevoli per aumentare la quantità di quelli che utilizzano abitualmente,
oppure chiedono/acquistano beni strumentali durevoli per rimpiazzare quelli
messi fuori uso dal processo produttivo.
In sintesi l'investimento è
l'acquisto di nuovi beni strumentali (nuovi impianti e macchinari, una maggiore
quantità di scorte in magazzino, ecc.).
❍ "Reddito monetario" e "reddito reale"
di un soggetto economico
● Il
"reddito monetario" di un soggetto
Si definisce "reddito
monetario" di un soggetto la quantità di denaro che questi guadagna annualmente
o comunque periodicamente.
● Il
"reddito reale" di un soggetto
Si definisce "reddito
reale" l'insieme dei beni che possono essere acquistati col reddito
monetario. Nei paesi primitivi alle persone viene dato direttamente reddito
reale, in quanto vangono pagati in natura (sacchi di fagioli, formaggi, chiodi,
pentole).
❍ "Reddito nazionale reale" e "reddito
nazionale monetario" di una intera nazione
● "Reddito
nazionale reale"
Si parla anche di "reddito
nazionale reale", intendendo la quantità di beni e servizi prodotti da una
nazione in un anno.
● "Reddito
nazionale monetario"
Il "reddito nazionale
monetario" non è altro, allora, che il valore in moneta del reddito
nazionale reale.
● La
"ricchezza"
Si definisce
"ricchezza" l'insieme dei beni già prodotto a disposizione di un
singolo soggetto o di una nazione. Mentre la ricchezza indica beni che già
esistevano all'inizio di un certo periodo, il reddito indica i beni di nuova
produzione che saranno creati in quel periodo.
I PROBLEMI DELLA SCIENZA ECONOMICA
❍ Comportamento del consumatore
E' la branca della economia che
si occupa di rispondere a domande del tipo:
In che modo le famiglie
scelgono i beni da consumare?
Conoscendo il prezzo di due
beni e il reddito della famiglia, possiamo ragionevolmente prevedere cosa
acquisterà e quanto risparmierà?
In un paese composto
prevalentemente di giovani il risparmio sarà più alto che in un paese con una
popolazione anziana?
Un paese arabo con la ricchezza
concentrata nelle mani della persona del sultano consumerà più beni di lusso di
un paese democratico che dispone della stessa ricchezza, ma ripartita equamente
tra i cittadini?
❍ Comportamento dell'imprenditore
E' la branca della economia che
si occupa di rispondere a domande del tipo:
In che modo gli imprenditori
scelgono la quantità di beni che produrranno?
In un paese come l'India, è più
probabile che scelgano di produrre tessuti utilizzando molti macchinari e pochi
operai, o viceversa?
Perché ci sono periodi in cui
gli imprenditori investono moltissimo e periodi in cui lasciano persino
logorare i beni capitali esistenti?
❍ Il funzionamento del mercato
E' la branca della economia che
si occupa di rispondere a domande del tipo:
Perché determinati beni
risultano molto costosi, mentre altri hanno un prezzo molto basso?
I consumatori possono sperare
di ottenere dagli imprenditori in un tempo ragionevole i beni desiderati al
prezzo che sarebbero disposti a pagare?
Le imprese possono manipolare
il mercato a danno dei consumatori?
❍ Gli alti e bassi della attività economica
E' la branca della economia che
si occupa di rispondere a domande del tipo:
Perché a periodi di prosperità
economica, con alti stipendi, possibilità di facile occupazione, ecc. seguono
sempre dei periodi di attività economica ridotta, con disoccupazione,
diminuzione della produzione, ecc.?
Perché nei periodi di
disoccupazione e ridotta attività economica si verifica anche un aumento dei
prezzi?
E' la branca della economia che
si occupa di rispondere a domande del tipo:
Perché certo sistemi economici
(Giappone, Corea del sud) crescono più velocemente degli altri?
Quali effetti sul sistema
economico ha una crescita troppo rapida del prodotto di un paese?
Perché molti paesi del terzo
mondo stentano ad industrializzarsi?
❍ La distribuzione del reddito
E' la branca della economia che
si occupa di rispondere a domande del tipo:
Perché un camionista o un
idraulico guadagnano più diun impiegato o di un professioinsta?
Perché bisogna pagare somme più
alte ai proprietari di certi appartamenti rispetto ad altri?
Che rapporto c'è tra una crisi
economica e i salari degli operai?
E' la branca della economia che
si occupa di rispondere a domande del tipo:
Perché i titoli in borsa sono
sottoposti ad oscillazione talvolta molto forti?
Quanta moneta circola in un
certo sistema, e che effetto ha l'aumentarne o diminuirne la quantità?
Come fa una banca che ha
depositi per soli 100 milioni a concedere prestiti per diversi miliardi?
❍ Il commercio internazionale e i
cambi
E' la branca della economia che
si occupa di rispondere a domande del tipo:
Perché certi paesi si
specializzano in determinate produzioni (scarpe, tessuti) mentre altri scelgono
prodotti diversi?
Per quale ragione una moneta
(es. sterlina) si apprezza nei confronti di un'altra moneta (lira)?
Per politica economica si
intende l'insieme degli interventi delle autorità (aumento delle tasse,
provvedimenti contro la disoccupazione) allo scopo di influenzare il sistema
economico (ad es.: per far aumentare la occupazione; per far diminuire
l'inflazione, ecc.).
Il termine "politica
economica" è anche usato per indicare quella branca della scienza
economica che si occupa di tali interventi, studiando gli strumenti a
disposizione delle autorità e i loro effetti, e rispondendo a domande del tipo:
E' meglio cercare di far
diminuire la inflazione aumentando le imposte o riducendo le spese pubbliche?
Che effetto avrebbe sui cambi
una diminuzione della quantità di moneta in circolazione?
Che effetto avrebbe sul tasso
di interesse a cui vengono concessi i prestiti la vendita di un milione di BOT
da parte dello stato?
IL
METODO DELL’ECONOMIA
❍ Possiamo prevedere
il comportamento economico degli esseri umani?
A prima vista sembrerebbe che
sia impossibile prevedere il comportamento degli esseri umani, che sono
creature dotate di una volontà libera; la situazione sembrerebbe ancora
peggiore nel caso di un gran numero di individui, di cui è impossibile
conoscere uno per uno preferenze, modi di pensare, ecc. e che cambiano nel
tempo (i membri di un gruppo sociale oggi non sono gli stessi di qualche anno
fa).
Tuttavia dobbiamo considerare
che l'uomo tende a comportarsi razionalmente. Questo tipo d'uomo, detto homo
oeconomicus ha un comportamento che in molte occasioni è prevedibile. Ad
esempio possiamo prevedere che se tutti i consumatori si comportano
razionalmente e un supermercato alza i suoi prezzi rispetto ad un altro,
situato nella stessa zona, tutti andranno a fare acquisti presso il secondo
supermercato.
Ma questo non è sufficiente:
come facciamo a conoscere quanta carne acquisteranno 1.000 consumatori
razionali di cui non conosciamo i gusti? In questi casi ci viene in aiuto la
cosiddetta "legge dei grandi numeri".
Per illustrarla, ricorriamo ad
un esempio. Supponiamo che un gruppo di statistici rilevi una volta al mese la
quantità consumata di carne di un certo numero di famiglie relativa agli ultimi
30 giorni.
Da quanto abbiamo detto
(imprevedibilità della scelta di un soggetto libero) è naturale attendersi
delle grosse oscillazioni nel consumo. Invece, considerando un campione sempre
più numeroso di famiglie si nota che le oscillazioni via via si riducono. Se
consideriamo un numero molto grande di consumatori (quale quello che troviamo
nei moderni mercati), esse sono quasi impercettibili.
Si può visualizzare tutto
questo in una tabella che in orizzontale riporti i mesi e in verticale il
numero differente di famiglie, e in ogni casella il consumo mensile
dell’aggregato
|
|
Gennaio |
Febbraio |
Marzo |
Aprile |
Maggio |
Giugno |
Luglio |
Agosto |
Settembre |
Ottobre |
Novembre |
Dicembre |
Media
dell’anno |
|
1
famiglia |
10 |
15 |
15 |
13 |
6 |
8 |
10 |
10 |
15 |
16 |
14 |
20 |
12,66 |
|
10
famiglie |
100 |
110 |
120 |
105 |
100 |
115 |
112 |
100 |
110 |
97 |
120 |
120 |
109,08 |
|
100
famiglie |
1.000 |
1.050 |
990 |
1.020 |
1.030 |
1.040 |
1.000 |
1.015 |
995 |
1.040 |
1.100 |
1.100 |
1.031,66 |
|
1.000
famiglie |
10.000 |
10.100 |
10.050 |
10.080 |
10.030 |
10.050 |
9.900 |
9.980 |
10.000 |
10.060 |
10.080 |
10.100 |
10.035,83 |
|
10.000
famiglie |
100.000 |
100.300 |
100.400 |
99.800 |
99.000 |
100.500 |
100.800 |
10.000 |
100.300 |
100.800 |
100.900 |
100.800 |
100.300 |
|
100.000
famiglie |
1.000.000 |
1.000.200 |
1.000.800 |
1.000.900 |
1.000.100 |
1.000.050 |
1.000.500 |
1.000.600 |
1.000.100 |
990.800 |
1.000.000 |
1.000.900 |
999.579,16 |
Esponiamo ora gli stessi dati
sotto forma di variazioni percentuali rispetto alla media annuale:
|
|
Gennaio |
Febbraio |
Marzo |
Aprile |
Maggio |
Giugno |
Luglio |
Agosto |
Settembre |
Ottobre |
Novembre |
Dicembre |
Media
delle variazioni |
|
1
famiglia |
-21,01% |
+18,48% |
+18,48% |
+2,68% |
-52,6% |
-36,8% |
-21,01% |
-21,01% |
+18,48% |
+26,38% |
+10,58% |
+57,97 |
|
|
10
famiglie |
-8,32% |
+0,84% |
+10,01% |
-3,74% |
-8,32% |
+5,42% |
+2,67% |
-8,32% |
+0,84% |
-11,07% |
+10,01% |
+10,01% |
|
|
100
famiglie |
-3,06% |
+1,77% |
-4,03% |
-1,13% |
-0,16% |
+0,80% |
-3,06% |
-1,61% |
-3,55% |
+0.80% |
+6,62% |
+6,62% |
|
|
1.000
famiglie |
-0,35% |
+0,63% |
+0,14% |
+0,44% |
-0,05% |
+0,14% |
-1,35% |
-0,5% |
-0,35% |
+0,24% |
+0,44% |
+0,63% |
|
|
10.000
famiglie |
-0,29% |
+0% |
+0,09% |
-0,49% |
-1,29% |
+0,19% |
+0,49% |
-0,29% |
+0% |
+0,49% |
+0,59% |
+0% |
|
|
100.000
famiglie |
+0,04% |
+0,06% |
+0,12% |
+0,13% |
+0,05% |
+0,04% |
+0,09% |
+0,10% |
+0,05% |
-0,87% |
+0,04% |
+0,13% |
|
Guardando la seconda tabella si
può osservare un fenomeno che gli statistici osservano tutti i giorni: le
variazioni rispetto alla media diventano sempre più piccole. Si tratta di una
legge assolutamente generale, applicabile ai consumatori come alle molecole di
un gas: è la ben nota "legge dei grandi numeri". Essa dice che il
risultato di un gran numero di eventi singoli, pur variando ogni volta che
l'insieme di eventi si ripete, varierà sempre meno quanti più eventi singoli
concorrono a formarlo.
Questo fenomeno è anche alla
base del sistema delle assicurazioni e delle pensioni: la percentuale di
persone che rimane in vita dopo i 65 anni varia di pochissimo, come pure quella
delle persone che rimangono in vita dopo i 70 anni, quella delle persone che
rimangono in vita dopo i 75 anni ecc.
I gestori dei fondi pensione
possono così offrire ai sopravvissuti una pensione più alta di quello che essi
hanno versato.
Supponiamo ad esempio che un
gestore di fondi pensione pattuisca di pagare, dopo i 75 anni, a coloro che
avranno versato per quella data 20 anni di contributi mensili, una pensione di
1000 € al mese. Supponiamo che tutti coloro che iniziano a pagare i contributi a
40 anni li paghino per 20 anni e che nessuno di loro muoia prima di aver
completato il pagamento dei contributi, a 60 anni.
Se il gestore delle pensioni sa
che di 10 persone in vita a 60 anni dopo i 75 anni rimangono in vita solo 5
persone, e dopo gli 85 anni non rimane in vita più nessuno, egli dovrà al più
pagare:
1000 · 12 (mesi) · 5 (persone)
· 10 (anni) = 600.000 €
Pertanto egli chiederà a
ciascuna delle 10 persone di pagare mensilmente:
60.000/(20 anni *12 mesi * 10
persone) = 250 €
contro i 500 € che avrebbe
chiesto se avesse considerato una sopravvivenza del 100% tra i 75 e gli 85
anni.
La legge dei grandi numeri gli
assicura che ciò che è avvenuto in passato (il numero dei sopravvissuti) non
cambierà in futuro, a patto che egli gestisca le pensioni di un gran numero di
persone.
Ma attenzione: la legge dei
grandi numeri non funziona se il numero delle persone che si assicurano presso
il gestore è molto basso: le statistiche dei sopravvissuti sono infatti stabili
perché si riferiscono a centinaia o migliaia di persone, altrimenti non lo
sono. Questa è una delle ragioni per cui nell’Ottocento fallirono i tentativi
di creare delle “società di mutuo soccorso” tra operai di una fabbrica, che
versavano dei contributi per prelevare poi in vecchiaia una pensione: il numero
estremamente basso (al massimo un centinaio) di persone che partecipavano a
questi fondi faceva sì che vi fossero grandi oscillazioni: era sufficiente che
per dieci anni il numero dei sopravvissuti dopo i 75 anni fosse molto alto, e
il fondo si trovava a dover pagare cifre molto alte per le pensioni. Questa
condizione di incertezza impediva ai
gestori delle società di mutuo soccorso di sfruttare la legge dei grandi
numeri, che invece poteva essere sfruttata dalle grandi compagne assicurative
private o dallo stato: per poter garantire una pensione fissa, essi erano
costretti a chiedere somme molto più alte delle società private o dello stato,
perché i margini di incertezza erano più alti.
Per fare un altro esempio,
potremmo considerare come “evento” il numero di “testa” uscito da 5 lanci di
una moneta, oppure il numero di “testa” uscito da 100 lanci di una moneta,
oppure il numero di “testa” ottenuto da un milione di lanci di una moneta: se
consideriamo ad es. 10 di questi “eventi” vediamo che il risultato di un
milione di lanci ripetuto 10 volte varia di molto poco, mentre il risultato di
5 lanci ripetuti 10 volte varia di molto.
Possiamo ancora pensare al
seguente esperimento: definiamo come “evento” il lancio di un dado
contemporaneamente da parte di un certo numero di studenti e “risultato
dell’evento” la somma dei punteggi di tutti i dadi. Se il gruppo di studenti è
poco numeroso (es. una sola classe che getta i dadi) le variazioni del
risultati saranno molto grandi; ma se prendessimo 1000, 10.000, 100.000
studenti che lanciano simultaneamente i dadi si vedrebbe che le variazioni dei
punteggi totali da un lancio all'altro si ridurrebbero fino quasi ad annullarsi.
Possiamo anche fare una
esercitazione per simulare il consumo di carne delle famiglie di Orbassano.
Ogni alunno rappresenta una famiglia: egli deve munirsi di una monetina, e ogni
volta che la lancia il risultato testa vorrà dire che nel mese considerato la
famiglia acquista 1 kg di carne, mentre il risultato croce vuol dire che in
quel mese la famiglia acquista zero kg di carne.
Lanciando la monetina per
dodici volte si ottengono i consumi di carne delle famiglie di Orbassano per
ogni mese del 1999.
Il gioco si riprende
raddoppiando il numero delle famiglie: ogni alunno getta ora la monetina due
volte ogni mese e rappresenta ora due famiglie. Possiamo immaginare di aver
preso in esame un paese più grande di Orbassano: ad esempio Rivoli.
Infine, quintuplichiamo il
numero delle famiglie (ogni alunno getterà ora la monetina 5 volte): è come se
considerassimo il consumo di un paese cinque volte più grande di Orbassano.
Si vedrà che i risultati
rispecchiano quelli della tabella che è riportata più sopra.
NOZIONI
MATEMATICHE DI BASE
❍ Il linguaggio della scienza economica
La scienza economica utilizza
vari tipi di linguaggio per descrivere i fatti e le teorie.
Vi è anzitutto il linguaggio
verbale o discorsivo: si utilizzano parole e non numeri o disegni.
Ma accanto al linguaggio
verbale abbiamo quello geometrico, costituito dai grafici, di cui parleremo tra
breve.
Vi è poi il linguaggio
strettamente matematico, che utilizza le tipiche espressioni analitiche per
esprimere i rapporti tra le grandezze economiche.
Infine, possono essere
utilizzati schemi, diagrammi di flusso, simboli come quelli di crescita e
decrescita di una grandezza, che possono essere classificati come linguaggio
grafico.
La descrizione di un fenomeno
economico fatta utilizzando un dato tipo di linguaggio è normalmente
sostituibile o combinabile con una descrizione fatta con un altro tipo di
linguaggio. Tuttavia, in determinati casi risulta più conveniente in assoluto
utilizzare un determinato tipo di linguaggio, come quello matematico. Ad
esempio, la espressione:
![]()
evita, sintetizzandolo con
maggiore chiarezza, un lungo discorso sugli effetti delle spese dello stato sul
reddito nazionale, ed è quindi preferita dagli economisti ad una esposizione
puramente discorsiva.
❍ Le coordinate
cartesiane e la rappresentazione geometrica di grandezze numeriche
Fissiamo nel piano due rette
orientate perpendicolari tra loro, chiamandole "assi cartesiani
ortogonali". Più precisamente chiamiamo una di esse "asse x o delle
ascisse" e l'altra "asse y o delle ordinate".
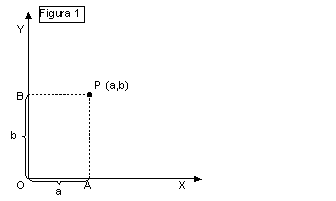
Preso ora un punto P qualunque
del piano, da esso si conducano le parallele agli assi, e diciamo A e B i loro
punti di intersezione con l'asse delle x e delle y rispettivamente (vedi figura
1). Fissata una unità di misura, diciamo a e b rispettivamente le misure dei
segmenti orientati OA e OB, cioè poniamo:
OA = a , OB = b
I due numeri così trovati si
dicono "coordinate cartesiane" del punto P. Precisamente: a si chiama
l'"ascissa" del punto P, b la "ordinata" di P. In tal modo
ad ogni punto del piano abbiamo associato due numeri reali. Viceversa, dati due
numeri reali a e b è sempre possibile determinare un punto ed uno solo che
abbia per ascissa a e per ordinata b. Infatti, preso sull'asse x il segmento
orientato OA di misura a e sull'asse y il segmento orientato OB di misura b, si
conduca da A la parallela all'asse y e da B la parallela all'asse x. Il punto P
di intersezione di queste due parallele è il punto cercato.
Concludendo: ad ogni punto del
piano corrisponde una coppia di numeri (detti le coordinate del punto) e ad
ogni coppia ordinata di numeri reali corrisponde u punto del piano, cioè il
punto che ha quei due numeri per coordinate. L'insieme dei due assi e della
unità di misura si dice "sistema di coordinate". I due assi dividono
il piano in quattro angoli o quadranti, che prendono il nome di primo, secondo,
tezo e quarto quadrante. Nella numerazione dei quadranti si comincia da quello
a destro in alto e si prosegue secondo il verso antiorario.
I punti del primo quadrante che
non stanno sugli assi, hanno ambedue le coordinate positive, quelli del secondo
quadrante hanno l'ascissa negativa e l'ordinata positiva, quelli del terzo
hanno ambedue le coordinate negative ed infine i punti del quarto quadrante
hanno l'ascissa positiva e l'ordinata negativa. Tutti i punti sull'asse x hanno
ordinata nulla, e tutti i punti sull'asse y hanno ascissa nulla. L'origine O ha
quindi nulla sia l'ascissa che l'ordinata.
Una variabile y si dice
funzione della variabile x quando esiste una legge di natura qualsiasi, la
quale faccia corrispondere ad ogni valore dato alla x uno e un solo valore
della y.
Per indicare che una variabile
y dipende da una variabile y si usano i simboli:
y =
f(x)
o
anche:
y =
y(x)
che si leggono tutti: "la
grandezza y è funzione della grandezza x"
Si parla di "funzioni di
più variabili" quando esiste una legge che permette di assegnare ai valori
di una coppia (terna, quaterna... ecc.) di variabili uno e un solo valore di
un'altra grandezza. Si scrive allora:
y = f(x,z,w,t)
per indicare che ad ogni
quaterna di valori delle variabili x, z, w, t è collegato uno ed un solo valore
della variabile y.
Quando esiste un complesso di
operazioni matematiche ben definite che permetta di passare dal valore della x
al valore corrispondente della y, come ad esempio nel caso
y = 3x4
si dice che la funzione è data
mediante una espressione analitica.
Se invece il rapporto tra la x
e la y può essere conosciuto solo sperimentalmente (cioè effettuando delle
misurazioni) si parla di funzioni empiriche.
Ad esempio: x = numero di
persone residenti in Italia; y = consumo annuale di gelati in italia.
Sinora abbiamo parlato di
"variabili". Per "variabile" si intende in matematica una
successione di numeri, ciascuno dei quali è chiamato "termine" di
quella variabile.
Gli economisti utilizzano,
accanto al termine variabile, quelli "quantità",
"grandezza", dato che le variabili da loro utilizzate si riferiscono
ad un determinato fenomeno della realtà, di cui misurano la quantità o
grandezza. Anche noi utilizzeremo d'ora in avanti i termini
"grandezza", "variabile", "quantità" come
sinonimi.
❍ La rappresentazione
geometrica di una funzione. Grafico di una funzione
Nello studio delle funzioni è
molto utile l'uso di una rappresentazone grafica che rende più chiare e
intuitive le considerazioni ad esse relative.
Precisamente: fissato sul piano
un sistema di assi cartesiani ortogonali, sia:
y = f(x)
una funzione che, per
semplicità, supponiamo definita in tutti i punti dell'intervallo (a,b).
Attribuendo alla x un valore
qualunque x1, compreso in (a,b), e dicendo y1 = f(x1)
il corrispondente valore di y, i due numeri (x1,y1)
saranno le coordinate di un punto P del piano. L'insieme di tutti i punti che
così si ottengono facendo variare la x nell'intervallo (a,b), cioè l'insieme di
tutti i punti del piano le cui coppie sono riportate nella tabella che esprime
la funzione, sarà un certo luogo geometrico che viene chiamato
"grafico" o "diagramma della funzione".
Molto spesso il diagramma è una
curva, composta cioè di un unico tratto, disegnabile senza staccare la penna
dal foglio, e in questo caso diremo che la equazione y = f(x) "è
l'equazione di una curva" o "rappresenta una curva".
Per "curva", nel significato
più generale che gli daremo, si deve intendere qualsiasi tipo di linea
continua, inclusa la retta, che non è altro, in fondo, che un caso particolare
di curva. In contrapposto alla retta parleremo, quando sarà necessario, di
“curve diverse da una retta".
Riassumendo: un grafico si
"costruisce" partendo da una tabella che esprima una funzione,
riportando in una colonna il valore della variabile indipendente e nell'altra
il valore corrispondente assunto dalla variabile dipendente. I valori di ogni
coppia vengono riportati ciascuno su uno degli assi, e il punto che nello
spazio cartesiano ha le coordinate corrispondenti a quei valori ci dà uno dei
punti del grafico. Un grafico viene in tal modo utilizzato per descrivere una
funzione. Notate che non è necessario disporre di una espressione analitica del
tipo:
y = 3 · x + 2
per poter creare una tabella.
Molto spesso gli economisti costruiscono una tabella a partire da osservazioni
della realtà. Si tratta in altre parole di quelle che abbiamo chiamato "funzioni
empiriche".
Come si rappresenta uno
spostamento sul grafico? Osserviamo la figura 3.
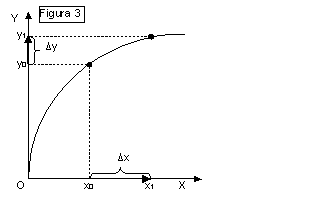
fissiamo anzitutto un punto
sull'asse delle ascisse, che individua il valore che la variabile indipendente
assume prima della variazione, e che chiameremo x0. Ad esso
corrisponde sull'asse delle ordinate un valore y0, che rappresenta
il valore della variabile dipendente prima che la variazione della x la facesse
a sua volta variare.
Successivamente facciamo
variare la grandezza x, portandoci ad es. ad x1. A tale nuovo punto
sull'asse orizzontale la tabella associa un diverso punto y1
sull'asse verticale. Il valore della variazione della x è dato da:
x1 - x0
ed è rappresentato, sull'asse
delle ascisse, da un segmento orientato (verso destra se x1 - x0
è positivo, verso sinistra se x1 – x0 è negativo) di
lunghezza pari allo spostamento, e di origine x0.
Il valore della variazione
della y è dato da:
y1 – y0
ed è rappresentato, sull'asse
delle ordinate, da un segmento orientato (verso destra se y1 – y0
è positivo, verso sinistra se y1 – y0 è negativo) di
lunghezza pari allo spostamento e di origine y0.
Il segno utilizzato per
rappresentare la variazione nel calcolo simbolico è la lettera greca "
Δ " ("delta"). Pertanto il segno
Δx
si leggerà "variazione
della grandezza x" o, più sinteticamente, "variazione di x".
Se è:
Δx = + 5
ciò vuol dire che la variabile
x è passata da un valore x0 ad un valore x1 = x0
+ 5: si parla pertanto di "incremento" della variabile x ed esso sarà
rappresentato da una freccia rivolta a destra di lunghezza pari a 5 unità che
parte dal punto x0.
Se invece è:
Δx = – 5
ciò vuol dire che la variabile
x è passata da un valore x0 ad un valore x1 = x0
– 5: si parla pertanto di "decremento" della variabile x ed esso sarà
rappresentato da una freccia rivolta a sinistra di lunghezza pari a 5 unità che
parte dal punto x0.
Lo studente non trascuri mai di
indicare il segno della variazione. Se il segno non è indicato si suppone
comunque che sia positivo.
Lo studente ricordi inoltre di
contrassegnare le coordinate delle grandezze prima della variazione con il
deponente "0" e le coordinate delle grandezze dopo la variazione con
il deponente "1".
In conclusione, la variazione
Δx di una grandezza x qualsiasi non è altro che la quantità (positiva o
negativa) che occorre sommare al valore di partenza x0 per arrivare al valore
finale x1.
Così, se:
x0 = 5
x1 = 7
si avrà
Δx = + 2
perché si deve avere:
5 + Δx = 7
da cui:
Δx = 7 -- 5 = + 2
Se invece
x0 = 7
x1 = 5
si avrà Δx = – 2
perché si deve avere:
7 + Δx = 5
da cui:
Δx = 5 – 7 = – 2
Da un grafico si possono
ricavare due tipi di informazione: a) che valore assume la variabile dipendente
quando la variabile indipendente assume a sua volta un valore; b) come si
modifica la variabile dipendente quando si modifica il valore della variabile
indipendente.
Da un unico grafico si possono
perciò ricavare due tabelle:
1) una tabella dei valori che
la variabile dipendente assume in corrispondenza di quelli della variabile
indipendente;
2) una tabella delle variazioni
della variabile dipendente in corrispondenza di (successive) variazioni della
variabile indipendente.
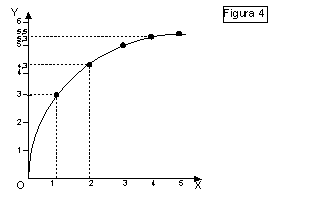
Consideriamo ad esempio il grafico
di figura 4, da cui si può ricavare la tabella che gli è riportata sotto, dei
valori di y corrispondenti a quelli di x.
|
X |
Y |
|
1 |
3 |
|
2 |
4,3 |
|
3 |
5 |
|
4 |
5,3 |
|
5 |
5,5 |
Nella tabella sottostante è
mostrata, sempre in riferimento al grafico di fig. 4, un’altra tabella, da cui
invece si ricava la relazione tra variazioni della x e variazioni della y: per
far ciò si considerano eguali variazioni successive (incrementi), ad esempio
unitarie, della variabile x a partire dal valore x = 0, e si cerca di
rispondere alla domanda: "se l'ascissa aumenta di 1, di quanto aumenta
l'ordinata?"
|
X0 |
ΔX |
ΔY |
|
|
0 |
+1 |
+3 |
Quando x passa da a 0 a 1 (Δx = +1)
y passa da 0 a 3 (Δy = +3) |
|
1 |
+1 |
+1,3 |
Quando x passa da 1 a 2 (Δx = +1) y
passa da 3 a 4,3 (Δy = +1,3) |
|
2 |
+1 |
+0,7 |
Quando x passa da 2 a 3 (Δx = +1) y
passa da 4,3 a 5 (Δy = +0,7) |
|
3 |
+1 |
+0,3 |
Quando x passa da 3 a 4 (Δx= +1) y
passa da 5 a 5,3 (Δy = +0,3) |
|
4 |
+1 |
+0,2 |
Quando x passa da 4 a 5 (Δx = +1) y
passa da 5,3 a 5,5 (Δy = +0,2) |
❍ La tangente ad una curva in un punto
La definizione di retta
tangente in un punto P è piuttosto semplice se ci si limita a casi particolari,
come quello del cerchio: è sufficiente definire la tangente come quella retta
che ha col cerchio un solo punto in comune, mentre la secante ha due punti in
comune (vedi figura).
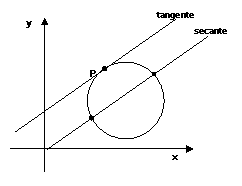
La tangente ha un solo punto in
comune con la curva, ma questa caratteristica non sempre è sufficiente ad
individuarla come nel caso di curve aperte, come mostra la figura sottostante,
in cui la retta r, pur avendo un solo punto in comune, non è la retta tangente:
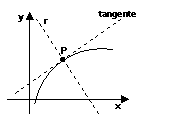
La definizione generale di
retta tangente ad una curva qualsiasi (che può in particolare essere aperta o
chiusa) richiede un altro metodo. Osserviamo la figura sotto riportata:
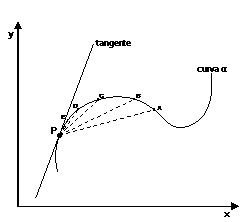
Proviamo a tracciare delle
corde dal punto P a punti sempre più vicini: otteniamo i segmenti PA, PB, PC,
PD, PE.
La posizione limite della corda
al tendere a P dell’altro estremo individua una direzione che è quella della
tangente.
Nella figura sottostante
vediamo che sia le corde il cui estremo si avvicina a P da sinistra (PF, PG,
PH, PJ, PK) che le corde il cui estremo si avvicina a P da destra (PA, PB, PC,
PD, PE) hanno la stessa posizione limite, individuata da un’unica tangente.
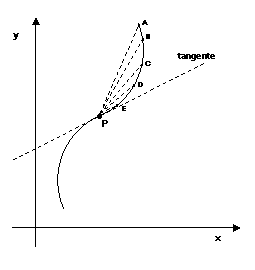
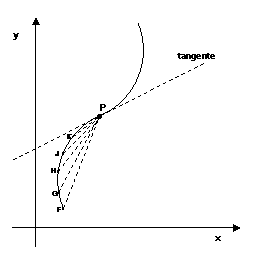
Ci sono dei casi in cui questo
procedimento delle corde sempre più corte aventi come punto comune P non
consente di individuare una tangente unica, ma esistono più tangenti (si
osservino le figure sottostanti).
Caso 1:
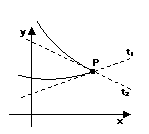
Caso 2:
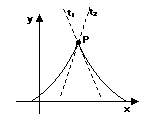
Caso 3:
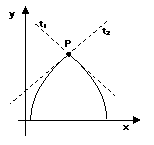
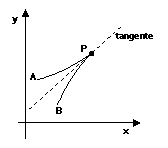
Qui sotto sono invece mostrati
casi in cui la posizione limite delle corde aventi come punto comune P è unica,
e quindi esiste un’unica tangente:
Caso 4:
Caso 5:
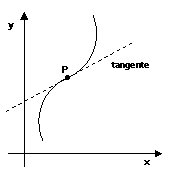
Caso 6:
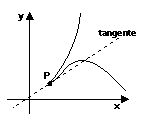
Caso 7:
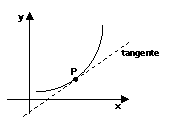
Caso 8:
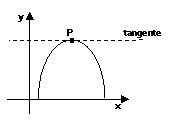
❍ La pendenza di una
curva. Pendenza finita e pendenza puntuale
Consideriamo la curva di figura
0509292128:
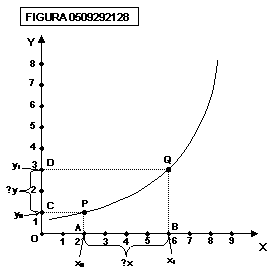
Si definisce “pendenza finita
relativa all’intervallo AB” o, equivalentemente, “pendenza finita relativa
all’arco PQ” il valore:
![]()
In altre parole, la pendenza
finita di una curva è il rapporto tra l’incremento della variabile riportata
sull’asse delle ordinate e quello della variabile riportata sull’asse delle
ascisse calcolato tra due punti distinti della curva.
Il valore della pendenza finita
dipende dall’arco considerato, ed è diversa se si considerano due archi
diversi, come è mostrato dalla figura 0509292151:
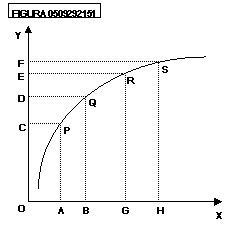
Se calcoliamo la pendenza
finita relativa all’arco PQ essa sarà diversa dalla pendenza finita relativa
all’arco RS:
![]()
dove i segmenti orientati AB e
GH rappresentano i due diversi ∆x, mentre i segmenti orientati CD ed EF
rappresentano i corrispondenti ∆y.
Come è noto allo studente, due
punti A e B sull’asse X possono individuare due distinti segmenti orientati, a
seconda di quale punto sia definito iniziale e di quale punto sia definito
finale. Se A è il punto iniziale e B il punto finale otteniamo il segmento AB,
che nella figura ha orientamento positivo (perché coincidente con
l’orientamento dell’asse X) e rappresenta un ∆x di segno positivo; se B è
il punto iniziale e A il punto finale otteniamo il segmento BA, che nella
figura ha orientamento negativo (perché contrario all’orientamento dell’asse X)
e rappresenta un ∆x di segno negativo. Lo stesso vale, sull’asse Y della
nostra figura, per i segmenti CD (orientamento positivo) e DC (orientamento
negativo).
La pendenza finita può essere
sia positiva sia negativa. Nella figura 0509301733 calcoliamo ad esempio la
pendenza relativa all’arco PQ:
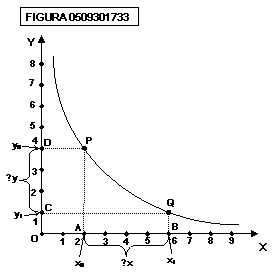
![]()
A differenza delle curve vere e
proprie, le rette hanno pendenza sempre eguale, indipendentemente dal segmento
considerato; nella figura 0509292159, a differenza che nella figura 0509292151,
la pendenza relativa all’arco (segmento) PQ è identica a quella relativa
all’arco (segmento) RS:
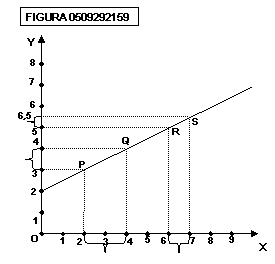
abbiamo infatti:
![]()
![]()
Si definisce “pendenza puntuale
nel punto P” la pendenza della retta tangente nel punto P. Nella figura 0509301730
la pendenza puntuale nel punto P è pari alla pendenza della retta r, che viene
calcolata relativamente al segmento PE (si ricordi che la pendenza di una retta
è sempre la stessa quale che sia il segmento considerato) cosicché è:
![]()

Calcoliamo la pendenza puntuale
nel punto P della curva della figura 0509301828:
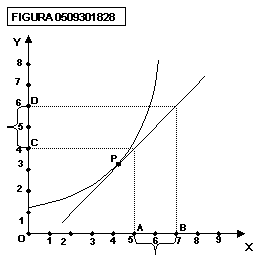
tale pendenza è pari a:
![]()
Calcoliamo la pendenza puntuale
nel punto P della curva della figura 0509301847:
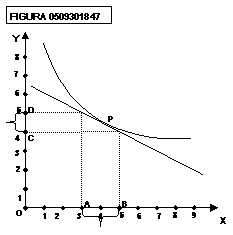
tale pendenza è pari a:
![]()
❍ Osserviamo la pendenza delle tangenti per determinare il
tipo di curva
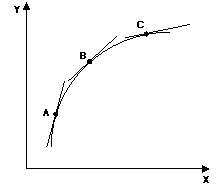
Nella curva sottostante, passando
dal punto A al punto C la pendenza della tangente, che è negativa in tutti e
tre i punti, diminuisce però in valore assoluto: si tratta quindi di una curva
a pendenza negativa e decrescente in valore assoluto
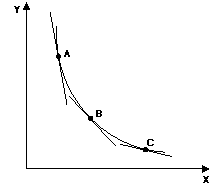
Nella curva sottostante,
passando dal punto A al punto C la pendenza della tangente, che è negativa in
tutti e tre i punti, cresce però in valore assoluto: si tratta quindi di una
curva a pendenza negativa e crescente in valore assoluto
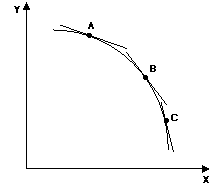
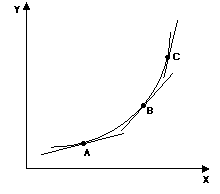
Nella curva sottostante,
passando dal punto A al punto C la pendenza della tangente, che è positiva in
tutti e tre i punti, diminuisce: si tratta quindi di una curva a pendenza
positiva e decrescente
Nella curva sottostante,
passando dal punto A al punto C l’inclinazione della tangente, che è positiva
in tutti e tre i punti, cresce: si tratta quindi di una curva a pendenza
positiva e crescente
❍ Classificazione
delle curve in base al diverso rapporto tra Δx e Δy
Nelle figura 9-16 che sono
riportate più sotto, per semplicità non compaiono valori numerici, bensì
segmenti orientati (frecce) riportati nelle relative tabelle.
Come si può vedere, ogni
grafico presenta un diverso tipo di rapporto tra variazioni della variabile x e
variazioni della variabile y.
❍ Curva di pendenza costante ed
eguale a zero
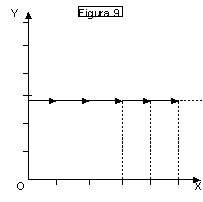
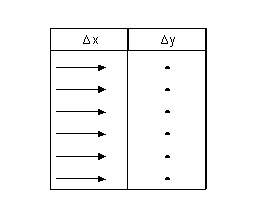
Il grafico di fig. 9 mostra che
eguali variazioni successive e positive della x a partire dal valore x = 0 non
provocano alcuna variazione della y (invece delle frecce sono stati riportati
dei punti, che per definizione geometrica hanno estensione pari a zero), che
rimane costante al valore y = n
Si tratta di una curva di
pendenza (puntuale) costante ed eguale a zero
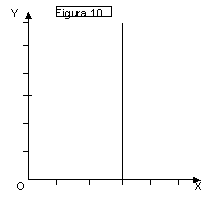
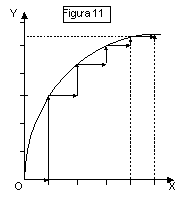
Il grafico di fig. 10 non
esprime una funzione (univalente), in quanto al valore x0
corrispondono infiniti valori della y. Tuttavia tale grafico può servire per
descrivere particolari situazioni dela realtà. Si pensi ad un elemento chimico
che formi composti solo ad una pressione pari ad x0. Un grafico che
riportasse (asse verticale) il numero dei composti di tale elemento in funzione
della pressione (asse orizzontale) avrebbe la forma della figura 11: esistono 0
composti per tutti i valori di pressione diversi da x0, e infiniti (o numerosi)
composti in corrispondenza del valore x0.
Si tratta di una curva (retta) di
pendenza infinita.
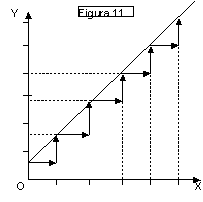
❍ Curva di pendenza positiva e
costante
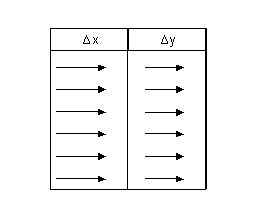
Il grafico di fig. 11 mostra
che ad eguali variazioni successive e positive della x a partire dal valore x =
0 corrispondono eguali variazioni successive e positive della y.
Si suol dire che tra le
grandezze x e y vi è un rapporto diretto (se x cresce anche y cresce e
viceversa)
Si tratta di una curva di
pendenza (puntuale) positiva e costante.
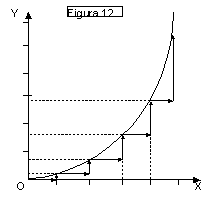
❍ Curva di pendenza positiva e
crescente
Il grafico di fig. 12 mostra
che ad eguali variazioni successive e positive della x a partire dal valore x =
0 corrispondono successive variazioni positive e crescenti della y
Tra le grandezze x e y sussiste
un rapporto diretto (se y cresce anche y cresce e viceversa).
Si tratta di una curva di
pendenza (puntuale) positiva e crescente.
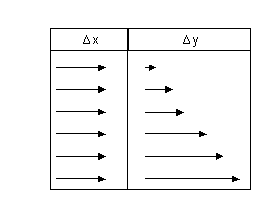
❍ Curva di pendenza positiva e
decrescente
Il grafico di fig. 11 mostra
che ad eguali variazioni successive e positive della x a partire dal valore x =
0 corrispondono successive variazioni positive e decrescenti della y
Tra le grandezze x e y sussiste
un rapporto diretto. (se x cresce anche y cresce; se una decresce anche l’altra
decresce)
Si tratta di una curva di
pendenza (puntuale) positiva e decrescente
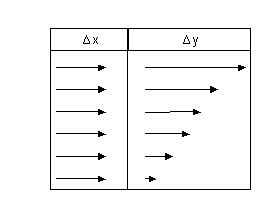
❍ Curva di pendenza negativa e
costante
Il grafico di fig. 12 mostra
che ad eguali variazioni successive e positive della x a partire dal valore x =
0 corrispondono eguali variazioni successive e negative della y
Si suol dire che tra le due
grandezze vi è un rapporto inverso (se x cresce y diminuisce; se x diminuisce y
cresce)
Si tratta di una curva di
pendenza (puntuale) negativa e costante.
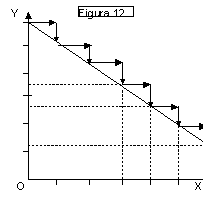
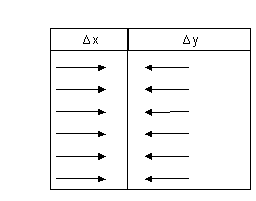
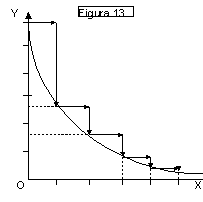
❍ Curva di pendenza negativa e decrescente in valore
assoluto
Il grafico di fig. 13 mostra
che ad eguali variazioni successive e positive della x a partire dal valore x =
0 corrispondono successive variazioni negative e decrescenti (in valore
assoluto) della y
Tra le due grandezze sussiste
un rapporto inverso.
Si tratta di una curva di
pendenza (puntuale) negativa e decrescente in valore assoluto
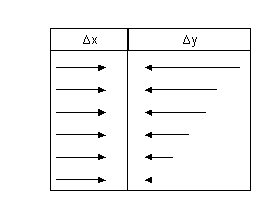
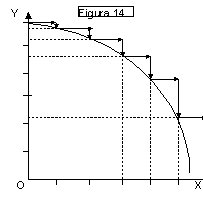
❍ Curva di pendenza negativa e crescente in valore assoluto
Il grafico di fig. 14 mostra
che ad eguali variazioni successive e positive della x a partire dal valore x =
0 corrispondono successive variazioni negative e crescenti (in valore assoluto)
della y
Tra le due grandezze sussiste
un rapporto inverso.
Si tratta di una curva di
pendenza (puntuale) negativa e crescente in valore assoluto
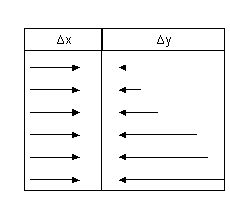
❍ Grafico del rapporto direttamente proporzionale tra due
grandezze
Il grafico di figura 15 è grafico
del rapporto direttamente proporzionale tra due grandezze: quando la variabile
x aumenta anche la variabile y aumenta della stessa proporzione; quando la
variabile x diminuisce, anche la variabile y diminuisce della stessa
proporzione. Tale rapporto è espresso dalla formula:
y = k · x
dove k è una costante che può
assumere qualsiasi valore
Nota bene: solo le rette che
passano per l’origine hanno per equazione y = k · x ed esprimono un rapporto
direttamente proporzionale. Le rette che non passano per l’origine hanno come
equazione:
y = k · x + b
dove b rappresenta l’intercetta
sull’asse verticale, e non esprimono un rapporto direttamente proporzionale
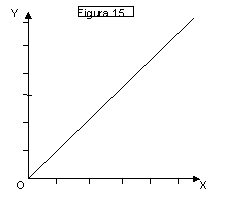
❍ Grafico del rapporto inversamente proporzionale tra due
grandezze
Il grafico della figura 16 è il
grafico di un rapporto inversamente proporzionale tra due grandezze: se la
variabile x aumenta (raddoppia, triplica…) , la variabile y diminuisce della
stessa proporzione (si riduce alla metà, ad un terzo…); se la variabile x
diminuisce (si riduce alla metà, ad un terzo…) la variabile y aumenta in
proporzione inversa (raddoppia, triplica…).
La formula che esprime un
rapporto inversamente proporzionale tra due grandezze è la seguente:
![]()
dove k è una costante che può
assumere qualsiasi valore.
Il grafico è quello di una
iperbole equilatera, di cui gli assi cartesiani costituiscono gli asintoti: la
linea si avvicina all’asse delle x senza mai toccarlo e così pure avviene per
l’asse delle y
❍ Riepilogo della classificazione delle curve
(A) Curva a pendenza negativa e decrescente in
valore assoluto (rapporto inverso tra x e y)
(ad eguali variazioni
successive e positive della x corrispondono variazioni negative della y decrescenti
in valore assoluto)
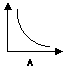
(A1) Iperbole equilatera (caso particolare della
curva A)
(rappresenta la formula: ![]() del rapporto
inversamente proporzionale)
del rapporto
inversamente proporzionale)

(B) Curva a pendenza negativa e decrescente in
valore assoluto (rapporto inverso tra x e y)
(ad eguali variazioni
successive e positive della x corrispondono variazioni negative della y
crescenti in valore assoluto)
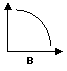
(C) Curva a pendenza negativa e costante
(rapporto inverso tra x e y)
(ad eguali variazioni
successive e positive della x corrispondono variazioni negative eguali tra
loro)
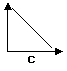
(D) Curva a pendenza positiva e decrescente
(rapporto diretto tra x e y)
(ad eguali variazioni
successive e positive della x corrispondono variazioni positive e decrescenti
della y)
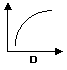
(E) Curva a pendenza positiva e crescente
(rapporto diretto tra x e y)
(ad eguali variazioni
successive e positive della x corrispondono variazioni positive e crescenti
della y)
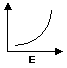
(F) Curva a pendenza positiva e costante
(rapporto diretto tra x e y)
(ad eguali variazioni
successive e positive della x corrispondono variazioni positive e costanti della
y)
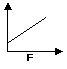
(G) Curva (grafico) del rapporto direttamente
proporzionale tra x e y
(le due grandezze sono legate
dalla formula y = k ‧ x)
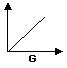
(H) Curva (retta) di pendenza zero (tra x e y non
vi è rapporto: se x varia, y non varia)
(variazioni successive e
positive della x non provocano alcuna variazione della y)
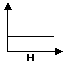
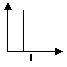
(I) Curva (retta) di pendenza infinita
❍ Calcoli con valori percentuali
Spesso gli economisti
utilizzano nelle loro descrizioni valori percentuali anziché valori assoluti.
Si noti che il termine
"valore assoluto" può avere due significati ben distinti:
(a) Per valore assoluto di un numero relativo x
si intende quello derivante dalla seguente trasformazione:
● se
x è positivo il valore assoluto è pari ad x
● se
x è negativo il valore assoluto è pari a – x
● se
x è zero il valore assoluto è zero
Così, il valore assoluto di +2
è +2, mentre il valore assoluto di – 5 è 5
Di solito, per indicare questo
tipo di valore assoluto, si fa precedere e seguire il numero da una sbarretta
verticale:
|x|
(b) Per valore assoluto di una grandezza in
contrapposto a valore percentuale si intende il valore non espresso in termini
percentuali
Ad esempio, se la produzione di
auto brasiliane è passata da 1000 unità a 2000 unità nel corso del 1991 si dirà
che l'aumento in valore assoluto è di 1000 unità, mentre in valore percentuale
è del 100%
Lo studente deve stabilire, in
base al contesto del discorso, a quale dei due significati si faccia
riferimento. Nel caso di dubbio chiederà chiarimenti all'insegnante.
Nel presente paragrafo,
"valore assoluto" di una grandezza sarà inteso nel significato (b),
in contrapposto cioè a "valore percentuale"
Lo studente deve essere in
grado di compiere le seguenti operazioni:
(1) Trasformare una frazione qualsiasi in un
valore percentuale
Si consideri la frazione![]() : facendo la proporzione si ottiene:
: facendo la proporzione si ottiene:
4 : 5 = x : 100
che si legge: “4 rappresenta
rispetto a 5 la stessa parte che x rappresenta rispetto a 100”. Dalla
proporzione si ottiene:
x = 80
per cui la nostra percentuale
sarà pari a ![]()
In pratica, è sufficiente moltiplicare
![]() · 100 per ottenere
· 100 per ottenere ![]()
(2) Conoscendo una variazione in valore
assoluto, tradurla in termini percentuali
Consideriamo la produzione di
auto brasiliana come sotto riportata:
Produzione 1990 = 2300 unità
Produzione 1991 = 2550 unità
E' evidente che la variazione
in valore assoluto della produzione è stata di:
2550 - 2300 = + 250 unità
Per trasformare questo valore
assoluto in valore percentuale occorre anzitutto stabilire il valore di
riferimento. Normalmente, se non viene detto diversamente, il valore di
riferimento di una variazione è il valore iniziale (nel nostro caso: 2300
unità).
La domanda è quindi: quanta
percentuale di 2300 rappresenta 250?
Per rispondere occorre
impostare la proporzione:
x : 100 = 250 : 2300
che si legge così: "x
rappresenta rispetto a 100 la stessa parte che 250 rappresenta rispetto a
2300"
Da ciò si ottiene:
![]()
Il metodo consiste quindi nel
moltiplicare ![]() per 100
per 100
(3) Determinare l'incremento (o decremento) di
una grandezza in valore assoluto conoscendone il valore percentuale.
Sia noto ad esempio che la
produzione brasiliana di auto nel 1991 è aumentata del 75% rispetto a quella
del 1990, che era di 3540 unità. Quante auto in più sono state prodotte nel
1991 rispetto al 1990?
Il calcolo è molto semplice, in
quanto basta moltiplicare il valore di riferimento (produzione 1990) per la
frazione che rappresenta la percentuale:
![]()
I RAPPORTI TRA I SOGGETTI DEL
SISTEMA ECONOMICO
❍ Il circuito famiglie-imprese. La legge di Say.
Osserviamo la figura 1, con lo
schema dei rapporti tra famiglie e imprese in un sistema economico semplificato:
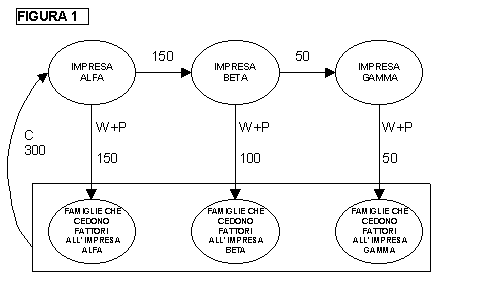
L’impresa Alfa produce
automobili, utilizzando lamiere che paga lire 150 all’impresa Beta.
L’impresa Beta produce lamiere,
utilizzando minerale che paga lire 50 all’impresa Gamma
L’impresa Gamma produce
minerale senza utilizzare beni strumentali acquistati da altre imprese
I beni finali prodotti dal
sistema economico consistono in auto per un valore di 300 lire, che
costituiscono l’incasso dell’impresa Alfa (freccia verticale dalle famiglie
all’impresa Alfa)
Ciascuna impresa, una volta
pagato il valore dei beni intermedi utilizzati, distribuisce tutto il rimanente
alle famiglie che hanno preso parte alla produzione, sotto forma di flusso W+P
di
● salari
● profitti
● stipendi
● interessi
● royalties
(compensi per i brevetti utilizzati)
● rendite
(compenso ai proprietari dei terreni, delle miniere e delle altre risorse
naturali utilizzate)
Tra le famiglie che hanno preso
parte alla produzione includiamo ovviamente anche quelle degli imprenditori.
Possiamo subito vedere che i
flussi W+P dalle imprese alle famiglie sono pari a 150+100+50 = 300, e cioè
hanno lo stesso valore del prodotto finale, costituito da automobili (300).
Ma in questo grafico è anche
vero che la produzione eguaglia la domanda aggregata (in questo caso la sola
domanda delle famiglie).
Per “valore aggiunto” di una
impresa si intende la differenza tra il ricavo o il costo dei beni strumentali
non durevoli impiegati. Tutto il valore aggiunto di una impresa va alle
famiglie. Il valore aggiunto di ciascuna impresa è quindi pari al flusso
verticale posto sotto di essa.
Come si vede, in una economia
chiusa, tre sono i concetti equivalenti che danno lo stesso valore:
▸ Valore dei beni finali prodotti
▸ Somma dei valori aggiunti
▸ Domanda aggregata
In sintesi, tutto il valore dei beni finali prodotti
dalle imprese nell’unità di tempo (mese, anno, etc.) viene distribuito alle
famiglie sotto forma di flusso W+P di salari, stipendi, profitto, royalties,
rendite.
Questo fatto risulta ancor
meglio da uno schema che riunisce in un unico gruppo le famiglie e in un unico
gruppo le imprese:
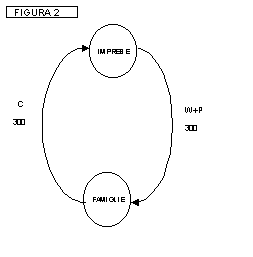
Osservando questo schema
notiamo che i salari e gli stipendi W+P distribuiti il 27 di ogni mese
finanziano le spese di consumo C delle famiglie fino al 27 del mese successivo,
quando i soldi sono rientrati tutti nelle casse delle imprese e il ciclo si
ripete.
Possiamo dire che le famiglie
acquistano i beni con gli stessi soldi che sono stati dati loro dagli
imprenditori per produrli. Questo fatto colpì l’economista classico
Jean-Baptiste Say (la scuola classica è la scuola di pensiero economico
dominante tra il 1790 e il 1850 circa, e comprende economisti come Say, Smith,
Ricardo, Marx), che formulò la legge degli sbocchi nella sua prima forma
(dovuta a Say): L’offerta (cioè la produzione) crea la sua domanda; in altre
parole gli imprenditori non hanno ragione di preoccuparsi che rimangano merci
invendute, perché è lo stesso denaro che essi distribuiscono alle famiglie che
consentirà ad esse di acquistarle.
Gli economisti neoclassici (la
scuola neoclassica è la scuola di pensiero economico dominante tra il 1850 e il
1930 circa) perfezionarono l’analisi di Say considerando anche la possibilità
che le famiglie potessero risparmiare. Essi misero a punto lo schema di figura
3 di un sistema economico con famiglie, banche e imprese:
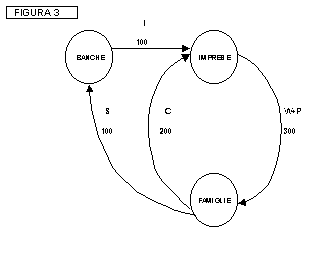
In questo schema tutto il
denaro risparmiato dalle famiglie (100) viene depositato nelle banche e poi
preso in prestito dagli imprenditori per acquistare beni strumentali durevoli e
scorte di beni strumentali non durevoli (flusso orizzontale I di investimenti
tra banche e imprese). In questo modo, le 300 lire distribuite dalle imprese il
27 del mese, alla fine del mese successivo ritornano nelle loro casse sotto
forma di flusso C+I, e il ciclo si ripete invariato. In questo caso si dice che
il sistema è in equilibrio.
Come possono essere sicuri i
neoclassici che tutte le somme risparmiate dalle famiglie torneranno alle
imprese sotto forma di investimenti? La risposta a questa obiezione è contenuta
nella legge degli sbocchi nella sua seconda forma (dovuta ai neoclassici):
Se le famiglie risparmiano più
di quanto gli imprenditori intendono investire, allora l’interesse offerto sui
capitali risparmiati si abbasserà e questo avrà l’effetto di far risparmiare
meno le famiglie, che aumenteranno le spese di consumo e di far aumentare gli
investimenti agli imprenditori. In tal modo, si raggiunge il punto in cui gli
imprenditori investono esattamente quanto le famiglie risparmiano. Anche in questo caso, tutta la produzione
ha trovato il suo sbocco, cioè è stata acquistata o dalle famiglie o dagli
imprenditori.
❍ I flussi tra i soggetti del sistema economico
Tra i soggetti economici vi
sono flussi reali (di beni e servizi) e flussi monetari (di denaro).
Solitamente, negli schemi che si trovano nei libri di economia i flussi
monetari sono rappresentati da una linea continua, mentre i flussi reali sono
rappresentati da una linea tratteggiata.
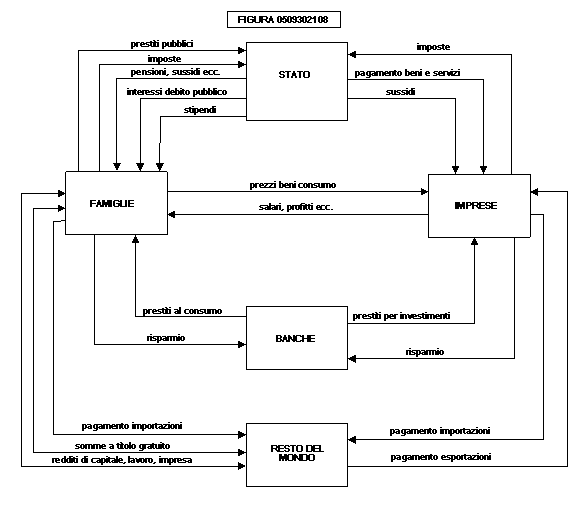
Osservando la figura 0509302108
possiamo notare i principali flussi del sistema:
● Dalle
imprese al resto del mondo
▸ Pagamento delle esportazioni
▸ Pagamento delle importazioni
● Dalle
imprese alle famiglie
▸ Compensi ai fattori produttivi (salari,
stipendi, profitti)
● Dalle
famiglie alle imprese, attraverso il mercato dei beni di consumo
▸ Ricavi delle vendite dei beni di consumo alle
famiglie
● Dalle
famiglie al resto del mondo
▸ Redditi di capitale, lavoro e impresa
dall’estero
Si tratta di somme che gli
stranieri ricevono dall’Italia per investimenti in imprese italiane o per
lavoro prestato in Italia
▸ Redditi di capitale, lavoro e impresa
all’estero
Si tratta di somme che gli
italiani ricevono dall’estero per investimenti in imprese estere o per lavoro
prestato all’estero
▸ Somme a titolo gratuito all’estero
Ad esempio la donazione via
internet che un italiano fa ad una fondazione di ricerca statunitense
▸ Somme a titolo gratuito dall’estero
Ad esempio le somme che gli
emigranti mandano in patria
● Dalle
famiglie alle imprese, attraverso le banche
▸ Risparmio familiare (il risparmio delle imprese
è molto modesto a paragone di quello delle famiglie)
● Dalle
famiglie e dalle imprese allo Stato (Bilancio pubblico)
▸ Imposte sulle imprese
▸ Imposte sul reddito
▸ Prestiti pubblici
● Dallo
Stato alle famiglie
▸ Compensi ai fattori (es. stipendi ai dipendenti
pubblici)
▸ Pensioni, sussidi di disoccupazione ecc.
Si tratta di somme che lo stato
preleva alle famiglie più ricche e redistribuisce alle famiglie più bisognose.
Si parla di spese di trasferimento.
▸ Interessi e rimborsi del debito pubblico
Lo Stato paga gli interessi e
restituisce le somme ricevute in prestito dalle famiglie
● Dallo
Stato alle imprese
▸ Acquisto di beni e servizi
▸ Sussidi alle imprese