|
IL
TEOREMA DI GÖDEL |
NOTAZIONI UTILIZZATE NELLA PRESENTE ESPOSIZIONE
DEFINIZIONE DI TEORIA ASSIOMATICA DEL PRIMO ORDINE
UN SISTEMA DI ASSIOMI PER L'ARITMETICA
FUNZIONI E RELAZIONI NUMERICHE
FUNZIONI
RICORSIVE PRIMITIVE E FUNZIONI RICORSIVE
ARITMETIZZAZIONE. I NUMERI DI GÖDEL.
IL TEOREMA DEL PUNTO FISSO. IL TEOREMA DI INCOMPLETEZZA DI GÖDEL
INDECIDIBILITA' RICORSIVA. TEOREMA DI CHURCH.
NOTAZIONI FREQUENTEMENTE UTILIZZATE NELLA
PRESENTE ESPOSIZIONE
▸ fbf sta per "formula
ben formata" del linguaggio ℒA
▸ B(x) indica una fbf che contiene,
tra i simboli di variabili non oggetto di quantificazione universale o
esistenziale la variabile x.
▸ ⊦S B(x) sta per "B(x) è un
teorema della teoria S"
▸ Il simbolo "◆" indica un metateorema, formulato in un
metalinguaggio che descrive la teoria
S anziché una formula nel linguaggio proprio
di tale teoria.
Il linguaggio che viene studiato (in questo caso ℒA) è chiamato linguaggio oggetto, mentre il linguaggio in cui formuliamo e
proviamo proposizioni circa il linguaggio oggetto è chiamato metalinguaggio. Il metalinguaggio
potrebbe anche essere formalizzato e essere soggetto di studio a sua volta,
studio che sarà condotto con un meta-metalinguaggio e così via. Per fare un
esempio di linguaggio oggetto e metalinguaggio, pensiamo ad un corso di
sanscrito. Il sanscrito è il linguaggio oggetto, mentre il metalinguaggio, il
linguaggio che usiamo per parlare del sanscrito è l'italiano. La distinzione
tra prova e metaprova (cioè una
prova nel metalinguaggio) conduce a una distinzione tra teoremi del linguaggio
oggetto e (meta)teoremi del metalinguaggio. Metamatematica è lo studio dei linguaggi oggetto logici e
matematici.
DEFINIZIONE DI TEORIA ASSIOMATICA DEL PRIMO
ORDINE
Una teoria formale S è definita quando sono
soddisfatte le seguenti condizioni:
▸ E' dato un insieme contabile (cioè finito o numerabile) di segni
come simboli di S. Una sequenza finita di simboli di S è chiamata espressione di S.
▸ Esiste un sottoinsieme dell'insieme delle espressioni
di S chiamato l'insieme delle formule
ben formate (fbf) di S. Deve
esistere una procedura definita per
stabilire se una data espressione è una fbf.
▸ C'è un insieme di fbf chiamate
l'insieme degli assiomi di S.
Deve esistere un modo per stabilire se una fbf è un assioma. In
tal caso S è chiamata teoria assiomatica.
▸ C'è un insieme finito R1, …, Rn di relazioni
tra fbf, chiamato regole di inferenza.
Per
ogni Ri c'è un unico intero positivo
j tale che, per ogni insieme di j fbf e ogni fbf B si può
stabilire se le j fbf date sono nella relazione Ri con B e, se è
così, B è detto seguire da o essere
una diretta conseguenza della
menzionata fbf in virtù di Ri.
Un esempio di regola di
inferenza è la regola modus ponens: C segue da B e da B ➙ C. Questa non è altro che una relazione
tra tutte le triple ordinate 〈B, B ➙ C, C〉 dove B e C sono fbf arbitrarie del sistema formale.
▸ Una prova è una sequenza B1, …, Bk
di fbf tale che, per ogni i, o Bi è un assioma
di S o Bi è una diretta conseguenza di qualcuna delle precedenti
fbf nella sequenza in virtù di una delle regole di inferenza di S.
▸ Un teorema di S è una fbf B di S tale che B è l'ultima
fbf di qualche prova di S. Tale prova
è chiamata prova di B in S.
Anche se S è assiomatico, cioè esiste una procedura
definita per stabilire se una qualsiasi fbf sia un
assioma, la nozione di "teorema" non è necessariamente definita dal
momento che, in generale, non c'è una procedura definita per
determinare, data una fbf B, se c'è una prova di B. Una teoria per
la quale esiste una tale procedura è chiamata teoria decidibile, altrimenti è teoria indecidibile.
Se una teoria è decidibile, idealmente una macchina logica può
essere creata per testare se le fbf sono teoremi
laddove, per una teoria indecidibile, è necessaria
la creatività del logico per stabilire se le fbf sono teoremi
▸ Una fbf è detta essere una conseguenza
in S di un insieme Γ di fbf se e solo se c'è una
sequenza B1, …, Bk di fbf tali che C è in Bk
e, per ogni i, o Bi è un'assioma o Bi appartiene a Γ
o è una diretta conseguenza, mediante qualche regola di inferenza, di qualcuna
delle precedenti fbf nella sequenza. Una tale sequenza è chiamata prova (o deduzione) di C da Γ.
I membri di Γ sono chiamati le ipotesi
o premesse della prova. Viene
utilizzata l'espressione "Γ ⊦ C" come abbreviazione per
"C è una conseguenza di Γ" e
talvolta "Γ ⊦S C" per indicare che la
deduzione avviene nel contesto della Teoria S.
Se Γ è un insieme finito possiamo
scrivere "{B1, …, Bm} ⊦ C" o "B1,
…, Bm ⊦ C". Se Γ
è l'insieme vuoto ∅ scriviamo "∅ ⊦ C" per indicare che C è
ovviamente un teorema. Normalmente, in questo caso, si omette il simbolo "∅" e si scrive
"⊦ C" per
indicare che C è un teorema.
▸ Per teoria del primo ordine
si intende una teoria formale le cui
fbf sono scritte impiegando i simboli del linguaggio logico del primo ordine,
come ad esempio:
∃x1 ∀x2 ∀x3 (R11(x1,0)
& R12(f12(x1,x2),x3))
Un linguaggio logico del primo ordine
impiega come simboli logici gli usuali connettivi logici "&", ➙", "∨", "⇔", ecc. e in più il
quantificatore universale "∀" e il quantificatore esistenziale "∃". Come simboli non
logici impiega i simboli Rmn di relazione, quelli fmn di funzione, le variabili
individuali xi e le costanti individuali ui. In un linguaggio logico del primo
ordine, a differenza che in un linguaggio
del secondo ordine, la quantificazione universale ed esistenziale è ammessa
solo in riferimento alle variabili individuali, mentre non è ammessa in
riferimento a proprietà o funzioni o formule.
UN
SISTEMA DI ASSIOMI PER L'ARITMETICA
Gli assiomi di Peano per la descrizione
dell'aritmetica sono i seguenti:
(P1) 0
è un numero naturale
(P2) Se
x è un numero naturale, c'è un altro numero naturale denotato con x' (e
chiamato il successore di x)
(P3) 0
≠ x' per ogni numero naturale x
(P4) Se x' = y' allora x = y
(P5) (Principio di induzione matematica) Se Q
è una proprietà che potrebbe o potrebbe non valere per ogni numero naturale e
se:
▸ 0 ha la proprietà Q
▸ Se un numero naturale x ha la proprietà Q allora x' ha la proprietà
Q
allora tutti i numeri naturali hanno la proprietà Q
Questi
assiomi, insieme ad un certo numero di concetti di teoria degli insiemi, possono
essere usati per sviluppare non solo la teoria dei numeri naturali, ma anche la
teoria dei numeri razionali, reali e complessi.
Tuttavia
questi assiomi utilizzano nozioni intuitive e non rigorosamente formulate come quella
di "proprietà", che impediscono una formalizzazione rigorosa.
Pertanto i matematici hanno costruito una Teoria
S del primo ordine basata sui postulati di Peano e adeguata per ottenere
tutti i risultati di base della matematica.
Il
linguaggio ℒA della teoria S
sarà chiamato il linguaggio
dell'aritmetica. ℒA ha un'unica lettera predicato A12.
Scriveremo t = s per A12(t,s). ℒA ha un'unica
costante individuale a1. Useremo 0 come notazione alternativa per a1.
Infine, ℒA ha tre lettere
funzioni f12, f12, f22.
Scriveremo t' invece di f11(t), (t + s) invece di f12(t,s)
e (t ⋅ s) invece di f22(t,s).
Gli assiomi propri di S sono:
(S1) x1 = x2 ➙ (x1 = x3
➙ x2 = x3)
(S2) x1 = x2 ➙ x1' = x2'
(S3) 0 ≠ x1'
(S4) x1' = x2' ➙ x1 = x2
(S5) x1 + 0 = x1
(S6) x1 + x2' = (x1
+ x2)'
(S7) x1 ⋅ 0 = 0
(S8) x1 ⋅ (x2)'
= (x1 ⋅ x2) + x1
(S9) B(0) ➙ (∀x B(x) ➙ B(x')) ➙ ∀x B(x)) per ogni fbf B(x) di S.
Chiameremo
(S9) principio di induzione matematica.
Si noti che (S9) non è un singolo assioma, ma uno schema di assiomi.
Una
teoria che ha gli stessi teoremi di S è spesso indicata come aritmetica di Peano o semplicemente
come PA.
Da (S9),
mediante MP, otteniamo la regola di
induzione:
B(0), ∀x B(x) ➙ B(x') ⊦S ∀x B(x)
◆ Dagli assiomi di Peano sono immediatamente
derivabili anche le regole dell'uguaglianza. Quindi S è una teoria con
identità.
Sia data
una interpretazione di S con i seguenti caratteri:
▸ il dominio è l'insieme degli interi non-negativi
▸ l'intero 0 è l'interpretazione del simbolo 0
▸ l'operazione successore (addizione di 1) è l'interpretazione della
funzione f11
▸ l'addizione e la moltiplicazione consuete sono le interpretazioni di
+ e ⋅
▸ l'interpretazione della lettera predicato = è la relazione identità
Questa
interpretazione è un modello normale di S, chiamato l'interpretazione standard o il modello
standard.
L'aumentata
astrattezza della matematica a partire dalla fine dell'Ottocento sollevò un
problema importante. Sorse infatti la questione se un dato insieme di
postulati, posti a fondamento di un sistema, sia coerente, in maniera tale cioè
che non sia possibile dedurre teoremi mutuamente contraddittori dai postulati
stessi. Il problema non sembra urgente quando si sceglie un insieme di assiomi
concernenti un gruppo ben definito e familiare di oggetti; in questo caso,
infatti, non solo è importante domandarsi, ma può anche essere possibile
accertarsi, se gli assiomi sono realmente veri riguardo a quegli oggetti. Dal
momento che gli assiomi euclidei erano ritenuti universalmente come
affermazioni vere sullo spazio (o sugli oggetti nello spazio), nessun
matematico, prima del diciannovesimo secolo, considerò mai la questione se un
giorno potessero venir dedotti dagli assiomi due teoremi contraddittori. La
base di questa fiducia nella coerenza della geometria euclidea è il sano
principio che affermazioni logicamente incompatibili non possono essere
simultaneamente vere; secondo questo principio, se un insieme di proposizioni è
vero (e tali erano considerati gli assiomi euclidei), allora queste
proposizioni sono mutuamente coerenti.
Se
riconosciamo l'interpretazione standard come modello per S, allora,
naturalmente, S é coerente. Tuttavia questo tipo di argomentazione semantica,
che implica ragionamenti di teoria degli insiemi, è considerato da alcuni
troppo insicuro per servire come base delle prove di coerenza. Perdipiù, il
lettore badi bene che qui non è stata provata in modo rigoroso che gli assiomi
di S sono veri nell'interpretazione standard; lo abbiamo solo considerato
intuitivamente ovvio. Per queste e altre ragioni, quando la coerenza di S viene
invocata nell'argomentazione di una prova (es. tramite la reductio ad absurdum) è pratica comune considerare l'affermazione
sulla coerenza di S come una assunzione esplicita non provata.
I termini
0, 0', 0'',… sarenno chiamati numerali
e denotati da 0̅, 1̅, 2̅, ecc. Più precisamente,
0̅ è 0 e, per ogni numero
naturale n, n̅+̅1̅ è (n̅)'.
◆ Qualsiasi modello di S è infinito
Per ogni numero cardinale ℵβ, S ha un modello
normale di cardinalità ℵβ.
In S è
introdotta una relazione di ordine:
t < s sta per ∃w (w ≠ 0 & w + t = s)
t ≤ s sta per t < s ∨ t = s
t > s sta
per s < t
t ≥ s sta per s ≤
t
t ≮ s sta per ∼(
t < s)
eccetera
◆ (principio di induzione
completa) ⊦S ∀z (z < x ➙ B(z)) ➙ B(x)) ➙ ∀x B(x)
(principio del numero
più basso o least number principle) ⊦S ∃x B(x) ➙ ∃y (B(y) & ∀z (z < y ➙ ∼B(z))): "se la
proprietà P vale per qualche numero naturale, allora esiste un numero più basso
che soddisfa P".
◆ (metodo della discesa
infinita) ⊦S ∀x B(x) ➙ ∃y (y < x & B(y)))
➙ ∀x ∼B(x)
Per
"t|s" intendiamo ∃z (s = t ⋅ z)
Utilizzando
la teoria S si può tradurre in S e provare qualsiasi risultato di aritmetica
elementare contenuto nei testi correnti. Tra le funzioni traducibili in S ci
sono funzioni numeriche come xy e x!
Alcuni
risultati aritmetici standard, come il teorema di Dirichlet, sono provati con
l'aiuto della teoria delle variabili complesse, e a tutt'oggi non si sa se di
tali teoremi esistono prove elementari
(cioè prove in S). La formulazione di alcuni risultati aritmetici coinvolge
concetti non-elementari, come la funzione logaritmica, e, tranne che in casi
speciali, questi risultati non possono neanche essere formulati in S.
Come vedremo
successivamente, ci sono fbf chiuse che non sono né provabili né non-provabili
in S, se S è coerente; dunque c'è una fbf che è vera nell'interpretazione
standard ma non è provabile in S. Vedremo anche che questa incompletezza di S non può essere
soltanto attribuita all'omissione di qualche assioma essenziale, ma ha cause
più profonde, che sono comuni anche ad altre teorie.
◆ Esistono modelli non-standard per S di qualsivoglia cardinalità ℵα
Esistono almeno 2ℵ0 modelli non-isomorfi di
S di cardinalità ℵα
FUNZIONI
E RELAZIONI NUMERICHE
Una funzione numerica è una funzione i cui
argomenti e i cui valori sono numeri naturali e una relazione numerica è una relazione
i cui argomenti sono numeri naturali. Ad esempio una moltiplicazione è
una funzione numerica a due argomenti, mentre l'espressione x + y < z
determina una relazione numerica a tre argomenti. Le funzioni e le relazioni
numeriche sono intuitive e non sono inserite in nessun sistema formale.
Sia K una
teoria nel linguaggio ℒA dell'aritmetica. Una relazione numerica R(x1,
…, xn) si dice relazione
esprimibile in K se e soltanto se esiste una fbf A(x1, …, xn)
di S con n variabili libere tali che: per ogni numero naturale k1,
…, kn,
(1) Se
R(k1, …, kn) è vera, allora ⊦S A(k̅1,…, k̅n)
(2) Se
R(k1, …, kn) è falsa, allora ⊦S ∼A(k̅1, …, k̅n)
Sia K una
teoria con identità nel linguaggio ℒA dell'aritmetica. Una
funzione numerica f(x1, …, xn) si dice funzione rappresentabile in K se e
soltanto se esiste una fbf A(x1, …, xn+1) di S con le
variabili libere x1, …, xn+1 tali che per ogni numero k1,
…, kn+1:
(1) se
f(k1, …, kn) = kn+1, allora ⊦S A(k̅1, …, k̅n, k̅n+1)
(2) ⊦S (E1 xn+1)
A(k̅1, …, k̅n, xn+1)
Se in
questa definizione si sostituisce al posto della (2) la
(2') ⊦S (E1 xn+1)
A(x1, …, xn, xn+1)
allora la
funzione si dirà fortemente
rappresentabile in S. Si noti che la (2') implica la (2). Perciò ogni
funzione fortemente rappresentabile è anche rappresentabile. L'inverso è
anch'esso vero:
◆ Se f(x1, …, xn) è rappresentabile in K, allora
è fortemente rappresentabile in K
Poiché si
tratta di proprietà equivalenti, d'ora in poi le utilizzeremo in modo
intercambiabile.
◆ Una funzione rappresentabile in K è rappresentabile in ogni
estensione di K
Se R(x1,
…, xn) è una relazione, allora la funzione caratteristica CR(x1, …, xn)
si definisce come quella funzione che ha valore 1 se R(x1, …, xn)
è vera, mentre ha valore 0 se R(x1, …, xn) è falsa.
◆ [1305221653] Data una teoria K con identità nel linguaggio ℒA tale che ⊦K 0 ≠ 1̅ allora una relazione numerica R(x1, …, xn)
è esprimibile in S se e soltanto se CR(x1, …, xn)
è rappresentabile in K
FUNZIONI
RICORSIVE PRIMITIVE E FUNZIONI RICORSIVE
Le
seguenti funzioni sono chiamate funzioni
iniziali.
(I) La
funzione zero, Z(x) = 0 per ogni x
(II) La
funzione successore, N(x) = x + 1
per ogni x
(III) La
funzione proiezione, Uin(x1,
…, xn) = xi per tutte le xi, …, xn
Le
seguenti sono regole per ottenere nuove funzioni da funzioni date:
(IV) Sostituzione:
f(x1, …, xn) = g(h1(x1,
…, xn), …, hm(x1, …, xn))
f si dice ottenuta per sostituzione dalle funzioni
g(y1, …, ym)
h1(x1,
…, xn)
………………
hm(x1,
…, xn)
La sostituzione vale anche nel caso che ogni hi
sia una funzione di una parte soltanto delle variabili.
(V) Recursione
f(x1, …, xn, 0) = g(x1, …,
xn)
f(x1, …,xn,
y +1) = h(x1, …, xn, y, f(x1, …, xn,y))
Se poniamo n = 0 abbiamo la formula ricorsiva consueta:
f(0) = k dove k è un
numero naturale fissato
f(y +1) = h(y, f(y))
Si dice che f è ottenuta da g e h (nel caso n = 0 dal solo h) per recursione. I
parametri della recursione sono x1, …, xn
(VI) μ-operatore ristretto
Sia g(x1, …, xn, y) una funzione tale
che per ogni x1, …, xn c'è almeno un y tale che g(x1,
…, xn y) = 0. Denotiamo con
μy(g(x1, …, xn, y) = 0) il minimo numero y tale che
g(x1, …, xn, y) = 0.
In generale, per ogni relazione R(x1, …, xn) denotiamo con μyR(x1, …, xn,
y) il minimo y tale che R(x1, …, xn, y) sia vero, se un
tale y esiste.
Se è f(x1, …, xn) = μy(g(x1, …, xn,
y) =0) allora si dice che f è ottenuto da g per mezzo del μ-operatore
ristretto se per ogni x1, …, xn esiste almeno un y tale
che g(x1, …, xn, y) = 0
Una
funzione si dice funzione ricorsiva
primitiva se e soltanto se può essere ottenuta dalle funzioni iniziali per
mezzo di un numero finito di sostituzioni (IV) e ricorsioni (V)
Una
funzione f si dice funzione ricorsiva
se e soltanto se può essere ottenuta dalle funzioni iniziali per mezzo di un
qualsiasi numero finito di sostituzioni (IV), ricorsioni (V) e μ-operatore
ristretto (VI).
◆ Ogni funzione ricorsiva primitiva è ricorsiva, mentre il contrario è
falso
◆ Sia g(y1, …, yk) una funzione ricorsiva
(primitiva). Siano x1, …, xn distinte variabili e
per 1 ≤ i ≤ k, sia zi una delle variabili x1,
…, xn. Allora la funzione f tale che f(x1, …, xn)
= g(z1, …, zk) è ricorsiva (primitiva).
Quest'ultimo
teorema consente di produrre nuove funzioni ricorsive con i seguenti metodi:
▸ Aggiunta di variabili fittizie:
f(x1, x2, x3) = g(x1, x3).
La variabile x2 è detta variable fittizia,
perché è irrilevante per il valore della funzione.
▸ Permutazione di variabili: f(x1, x2, x3)
= g(x3, x1, x2)
▸ Identificazione di variabili: f(x1, x2) = g(x1,
x2, x1)
◆ La funzione zero è ricorsiva primitiva
◆ La funzione costante Ckn(x1, …, xn)
= k con k numero naturale fissato, è ricorsiva primitiva
Ecco un elenco esemplificativo
di funzioni ricorsive primitive:
▸ x + y
▸ x ⋅ y
▸ xy
▸ La funzione predecessore:
δ(x)![]()
▸ x ∸ y![]()
▸ |x – y|![]()
▸ sg(x) ![]()
▸ s̅g̅(x) ![]()
▸ x!
▸ min(x1, …, xn)
▸ max(x1, …, xn)
▸ rm(x,y) = resto della
divisione di y per x
▸ qt(x,y) = quoziente della
divisione di y per x
▸ Definizioni di somme limitate
e prodotti limitati.
▸ ![]()
▸ ![]()
▸ ![]()
▸ ![]()
Possiamo
anche definire somme doppiamente
limitate e prodotti doppiamente
limitati in termini di quelli già dati; per esempio:
![]()
◆ Se f(x1, …, xn, y) è ricorsiva primitiva
(ricorsiva), allora tutte le somme e i prodotti limitati definiti come sopra
sono ricorsive primitive (ricorsive)
Date
delle espressioni per relazioni numeriche possiamo applicare i connettivi del calcolo
proposizionale ad esse per ottenere nuove espressioni per relazioni. Per
esempio, se R1(x,y) e R2(x,u,v) sono relazioni, allora R1(x,y)
& R2(x,u,v) è una nuova relazione tra x,y,u,v.
Useremo ∀yy<z
R(x1, …, xn, y) per esprimere la relazione: "per tutti
gli y, se y è minore di z, allora vale R(x1, … xn,
y)". Useremo ∀yy≤z, ∃yy<z, ∃yy≤z in modo analogo. Chiameremo questi
quantificatori quantificatori limitati.
Definiamo
un μ-operatore ristretto:
![]()
Il valore
z è stato scelto nel secondo caso perché è più conveniente in prove successive;
questa scelta non ha significato intuitivo.
Definiamo
pure:
μyy≤ z+1 R(x1, …, xn, y) = μyy<z+1 R(x1, …, xn, y)
Una
relazione R(x1, …, xn) è detta relazione ricorsiva primitiva (o relazione ricorsiva) se e soltanto se la sua funzione
caratteristica CR(x1, …, xn) è ricorsiva
primitiva (o ricorsiva). In particolare, un insieme A di numeri naturali è un insieme ricorsivo primitivo se e
soltanto se la sua funzione caratteristica CA(x) è ricorsiva primitiva
(o ricorsiva).
◆ Relazioni ottenute da relazioni ricorsive primitive (ricorsive) per
mezzo dei connettivi proposizionali e i quantificatori sono anch'esse ricorsive
primitive (ricorsive).
Applicazioni dei μ-operatore limitati μyy<z
e μyy≤z conducono da relazioni ricorsive primitive
(ricorsive) a funzioni ricorsive primitive (ricorsive)
Per x
> 0 sia ℓℏ(x) il numero degli
esponenti non-zero nella fattorizzazione di x in potenze di primi o,
equivalentemente, il numero di primi che divide x.
Ogni
intero positivo x ha una fattorizzazione unica in potenze di numeri primi. Se
il numero:
x = 2a03a1…pkak
è usato
per "rappresentare" o "codificare" la sequenza di interi
positivi a0, …, ak, e il numero:
y = 2b03b1…pmbm
"rappresenta"
la sequenza b0, …, bm, allora il numero:
x
* y = 2a03a1 … pkakpk+1b0pk+2b1
… pk+1+mbm
"rappresenta"
la nuova sequenza a0, …, ak, b0, …, bm
ottenuta giustapponendo le due sequenze.
Qui (y)j
è usato per indicare bj quando y = 2b03b1…pmbm
"rappresenta" la sequenza b0, …, bm
◆ Sia
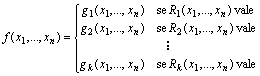
Se le funzione g1, …, gk e le
relazioni R1, …, Rk sono ricorsive primitive (ricorsive)
e se, per ogni x1, …, xn esattamente una delle relazioni
R1(x1, …, xn), …, Rk(x1,
…, xn) è vera, allora f è ricorsiva primitiva (ricorsiva)
E' essenziale
per quanto seguirà definire funzioni attraverso un tipo di ricorsione in cui il
valore f(x1, …, xn, y + 1) dipende non solo da f(x1,
…xn, y) ma anche da più di uno o da tutti i valori di f(x1,
…, xn, u) con u ≤ y. Questo tipo di ricorsione è chiamato ricorsione course-of-values. Sia
f#(x1, …, xn,y) = ∏u<ypuf(x1,
…, xn,u)
Si noti
che f può essere ottenuto da f# come segue:
f(x1,
…, xn,y) = (f#(x1, …, xn, y + 1))y.
◆ (ricorsione course of values) Se h(x1,
…, xn, y, z) è ricorsiva primitiva (ricorsiva) e
f(x1,
…, xn, y) = h(x1, …, xn, y, f#(x1, …, xn, y))
allora f è ricorsiva
primitiva (ricorsiva)
◆ (ricorsione course-of-values per le relazioni)
Se H(x1, …, xn, y, z) è una relazione
ricorsiva primitiva (ricorsiva) e R(x1, …, xn, y) vale se
e soltanto se vale
H(x1, …, xn,
y,(CR)#(x1,
…, xn, y))
dove CR
è la funzione caratteristica di R, allora R è ricorsivo primitivo (ricorsivo).
◆ (β-funzione di Gödel) Sia β(x1, x2, x3) = rm(1 +
(x3 +1) ⋅ x2, x1).
Allora β
è ricorsiva primitiva perché rm è ricorsiva primitiva. β è anche
fortemente rappresentabile in S dalla seguente fbf Bt(x1, x2, x3, y):
∃w(x1 = (1 + (x3 + 1) ⋅ x2) ⋅
w + y & y < 1 + (x3 + 1) ⋅
x2)
◆ Per ogni sequenza di numeri naturali k0, …, kn,
ci sono due numeri naturali b,c tali che β(b,c,i) = ki per 0
≤ i ≤ n
◆ Ogni funzione ricorsiva è rappresentabile in S
◆ Ogni relazione ricorsiva è esprimibile in S
Chiamiamo
relazione aritmetica una relazione
che è l'interpretazione di una qualche fbf B(x1, …, xn)
nel linguaggio ℒA dell'aritmetica
rispetto al modello standard
◆ Ogni relazione ricorsiva è aritmetica.
ARITMETIZZAZIONE.
I NUMERI DI GÖDEL.
Per una
arbitraria teoria K del primo ordine, colleghiamo a ciascun simbolo u di K un intero
positivo dispari g(u), chiamato il numero
di Gödel di u o il godeliano di u, nel seguente modo:
g( ( ) =
3
g( ) ) =
5
g( , ) =
7
g( ∼ ) = 9
g( ➙ ) = 11
g( ∀ ) = 13
g(xk)
= 13 + 8k per k ≥ 1
g(ak)
= 7 + 8k per k ≥ 1
g(fkn)
= 1 + 8(2n3k) per
k ≥ 1
g(Akn)
= 3 + 8(2n3k)
per k ≥ 1
Chiaramente,
ogni numero di Gödel di un simbolo è un intero positivo dispari. Perdipiù, quando diviso per 8, g(u) produce un resto di 5
quando u è una variabile, un resto di 7 quando u è una costante individuale, un
resto di 1 quando u è una lettera funzione e unr esto di 3 quando u è una
lettera predicato. In tal modo, differenti simboli hanno numeri di Gödel
differenti.
Data
un'espressione u0u1, …, ur dove ogni uj
è un simbolo di K, definiamo il suo numero di Gödel g(u0u1…ur)
mediante l'equazione:
g(u0u1…ur)
= 2g(u0)3g(u1)… prg(ur)
dove pj denota
il j-esimo numero primo e assumiamo che p0 = 2
Espressioni
differenti hanno numeri di Gödel differenti, in virtù della unicità della
fattorizzazione degli interi in numeri primi. Inoltre, le espressioni hanno
numeri di Gödel diversi da quelli dei simboli, dato che le prime hanno numeri
pari e i secondi numeri dispari. E' importante notare che un singolo simbolo,
considerato come espressione, ha un numero di Gödel differente dal suo numero
come simbolo. Per esempio, il simbolo x1 ha come numero di Gödel 21,
mentre l'espressione coerente nel solo simbolo x1 ha numero di Gödel
221.
Se e0,
e1, …, er è una sequenza finita di espressioni di K,
possiamo assegnare un numero di Gödel a questa sequenza ponendo:
g(e0,
e1, …, er) = 2g(e0)3g(e1)… prg(er)
Successioni
differenti di espressioni hanno numeri di Gödel differenti. Dal momento che il
numero di Gödel di una sequenza di espressioni
è pari e l'esponente di 2 nella sua fattorizzazione in primi è anch'esso
pari, differisce dai numeri di Gödel dei simboli e delle espressioni. Si
ricordi che una prova in K è un certo tipo di sequenza finita di espressioni e,
dunque, ha un numero di Gödel.
Pertanto
g è una funzione bijettiva dall'insieme dei simboli di K, espressioni di K e
sequenze finite di espressioni di K, nell'insieme degli interi positivi. Il
codominio di g non è l'intero insieme degli interi positivi. Per esempio, 10
non è un numero di Gödel.
Questo
metodo di associare numeri con simboli, espressioni e successioni di
espressioni fu elaborato originariamente da Kurt Gödel nel 1931 per aritmetizzare la metamatematica, cioè
per rimpiazzare asserzioni intorno un sistema formale da asserzioni numeriche
equivalenti e poi esprimere queste asserzioni entro il sistema formale stesso.
Questa idea si è rivelata fondamentale in logica matematica per la risoluzione
di numerosi problemi.
L'assegnazione
dei numeri di Gödel
qui esposta non è l'unico modo possibile di assegnare numeri. Altri metodi sono
esposti in Kleene, Introduction to
Metamathematics, Van Nostrand, 1952, e Smullyan, Theory of Formal Systems, Princeton University Press, 1965.
Una aritmetizzazione
di una teoria K è una funzione bijettiva g dall'insieme dei simboli di
K, espressioni di K e sequenze finite di espressioni di K nell'insieme degli
interi positivi. La funzione g deve soddisfare le seguenti condizioni:
▸ g è effettivamente computabile
▸ c'è una procedura effettiva per stabilire se un dato intero positivo
m è nel codominio di g e, se m è nel codominio di g, per trovare l'oggetto x
tale che g(x) = m
Una
teoria K è detta avere un vocabolario
ricorsivo primitivo (vocabolario
ricorsivo) se le seguenti proprietà sono ricorsive primitive (ricorsive):
▸ IC(x) : "x è il numero
di Gödel di una costante individuale di K"
▸ FL(x) : "x è il
numero di Gödel di una lettera funzione di K"
▸ PL(x) : "x è il
numero di Gödel di una lettera predicato di K"
Si ricordi che una funzione si dice funzione ricorsiva primitiva se e
soltanto se può essere ottenuta dalle funzioni iniziali per mezzo di un numero
finito di sostituzioni (IV) e ricorsioni (V)
Si ricordi che una funzione f si dice funzione ricorsiva se e soltanto se può
essere ottenuta dalle funzioni iniziali per mezzo di un qualsiasi numero finito
di sostituzioni (IV), ricorsioni (V) e μ-operatore ristretto (VI).
Si ricordi che una relazione R(x1, …,
xn) è detta relazione
ricorsiva primitiva (o relazione
ricorsiva) se e soltanto se la sua funzione caratteristica CR(x1,
…, xn) è ricorsiva primitiva (o ricorsiva). In particolare, un
insieme A di numeri naturali è un insieme
ricorsivo primitivo se e soltanto se la sua funzione caratteristica CA(x)
è ricorsiva primitiva (o ricorsiva).
◆ Qualsiasi teoria K che ha solo un numero finito di costanti
individuali, lettere funzione e lettere predicato ha un vocabolario ricorsivo
primitivo. In particolare, qualsiasi teoria K nel linguaggio ℒA dell'aritmetica
ha un vocabolario ricorsivo primitivo. In particolare, S ha un vocabolario
ricorsivo primitivo.
◆ [1305221913]
Sia K una teoria con
un vocabolario ricorsivo primitivo (ricorsivo). Allora le seguenti relazioni e
funzioni sono ricorsive primitive (ricorsive). In ciascun caso forniamo per
prima la notazione e la definizione intuitiva, e poi la formula equivalente da
cui può essere dedotta la ricorsività primitiva (ricorsività).
▸ EVbl(x) : "x è il
numero di Gödel di una espressione coerente in una variabile"
∃zz<x (1 ≤ z & x = 213+8z
▸ EIC(x) : "x è il
numero di Gödel di una espressione coerente in una costante individuale"
∃yy<x (IC(y) & x = 2y)
▸ EFL(x) : x è il numero di
Gödel di una espressione consisente in una lettera funzione"
∃yy<x (FL(y) & x = 2y)
▸ EPL(x) : "x è il
numero di Gödel di una espressione coerente in una lettera predicato
∃yy<x (PL(y) & x = 2y)
▸ ArgT(x) =
(qt(8,x ∸
1))0 : "Se x è il numero di Gödel di una lettera funzione fjn
allora ArgT(x) = n"
Si tenga qui presente che il numero di Gödel di una funzione
fkn è 1 + (2k3n); perciò qt(8,x ∸ 1) = (2n3k),
e poiché (y)j
indica bj quando y = 2b03b1…pmbm
"rappresenta" la sequenza b0, …, bm allora
(qt(8,x ∸
1))0 = (2n3k)0 = n
▸ Gd(x) : "x è il
numero di Gödel di una espressione di K"
EVbl(x) ∨ EIC(x) ∨ EFL(x) ∨ EPL(x) ∨ x = 23 ∨ x = 25 ∨ x = 27 ∨ x = 29 ∨ x = 211 ∨ x = 213 ∨ ∃uu<x ∃vv<x (x =
u * v & Gd(u) & Gd(v))
"x è il numero (di Gödel) di una variabile o il numero
di una costante individuale o il numero di una lettera funzione o il numero di
una lettera predicato o è il numero di "(" o è il numero di
")"… o è il numero di "∀" o esistono due numeri di Gödel di
due espressioni con numeri di Gödel rispettivamente u,v inferiori a x tali che
x è la giustapposizione di tali espressioni"
Compare qui un esempio di proprietà ricorsiva, anziché una funzione ricorsiva. La proprietà dipende dall'esistenza della
proprietà per valori inferiori ad x.
▸ MP(x,y,z) :
"L'espressione con numero di Gödel z è una diretta conseguenza delle
espressioni con numeri di Gödel x e y tramite applicazione di modus ponens"
y = 23 * x * 211 * z * 25
& Gd(x) & Gd(z)
▸ Gen(x,y) :
"L'espressione con numero di Gödel y proviene dall'espressione con numero
di Gödel x tramite la regola di generalizzazione"
∃vv<y (EVbl(v) & y = 23 * 23
* 213 * v * 25 * x * 25 & Gd(x))
▸ Trm(x) : "x è il
numero di Gödel di un termine di K".
Questa proprietà vale quando e solo quando o x è il
godeliano di una espressione coerente in una variabile o in una costante
individuale o c'è una lettera funzione fkn e termini t1,
.., tn tali che x è il godeliano di fkn(t1,
…, tn). Quest'ultima proprietà vale se e soltanto se c'è una
sequenza di n + 1 espressioni
fkn(
fkn(t1,
fkn(t1,
t2,
…
fkn(t1,
…, tn-1,
fkn(t1, …, tn-1,
tn)
l'ultima delle quali, fkn(t1,
…, tn), ha godeliano = x. Chiaramente,
y < 2x3x … pnx
= (2 ⋅ 3 ⋅ … ⋅ pn)x < (pn!)x
< (px!)x
Notare che ℓℏ(y) = n + 1 e anche che
n = ArgT((x))0, dal momento che (x)0 è il
godeliano di fkn. Quindi Trm(x) è equivalente alla
seguente formula:
EVbl(x) ∨ EIC(x) ∨ ∃yy<(px!)^x [x = (y)ℓℏ(x)∸1 &
ℓℏ(y) = ArgT((x)0
+ 1 & FL(((y)0)0) & ((y)0)1
= 3 & ℓℏ(y)0 = 2 & ∀uu<ℓℏ(y)∸2 ∃vv<x ((y)u+1 = (y)u * v
* 27 & Trm(v)) & ∃vv<x ((y)ℓℏ(y)∸1 =
(y)
ℓℏ(y)∸2 * v * 25
& Trm(v))]
"x è il godeliano di una variabile, o x è il godeliano
di una costante individuale, o esiste un godeliano tale che x è l'esponente del
penultimo (ℓℏ(x)∸1)"
Esponiamo in forma leggermente diversa la formula:

(dove il
segno "–" va letto come "∸", per mancanza in Microsoft Equation del simbolo
corrispondente)
▸ Atfml(x) : "x è il
godeliano di una fbf atomica di K"
Questo è
vero se e solo se ci sono termini t1, …, tn e una lettera
predicato Akn tale che x è il godeliano di Akn(t1,
…, tn). L'ultima asserzione vale sse c'è una sequenza di n + 1
espressioni
Akn(
Akn(t1,
Akn(t1, t2,
…
Akn(t1, …, tn-1,
Akn(t1,
…, tn-1, tn)
l'ultima
delle quali, Akn(t1, …, tn-1, tn),
ha godeliano x. Questa sequenza di espressioni può essere rappresentata dal suo
godeliano y. Chiaramente, y < (px!)x (vedi analoghe
considerazioni per Trm(x)) e n = ArgP((x)0). Così,
Atfml(x) è equivalente alla formula seguente:

▸ Fml(y) : "y è il
godeliano di una formula di K"
Atfml(y) ∨ ∃zz<y[Fml(z)
& y = 23 * 29 * z * 25) ∨ (Fml((z)0)
& Fml(z)1) & y = 23 * (z)0 * 211
* (z)1 * 25) ∨ (Fml((z)0) & EVbl((z)1)
& y = 23 * 2*3* * 213 * (z)1 * 25
* (z)0 * 25)]
▸ Subst(x,y,u,v) : "x è il godeliano del risultato della
sostituzione nella espressione con godeliano y del termine con godeliano u per
tutte le occorrenze liberre della variabile con godeliano v
▸ Sub(y,u,v) : "il godeliano del risultato della
sostituzione del termine congodeliano u per tutte le occorrenze libere
nell'espressione con godeliano y della variabile con godeliano v"
▸ Fr(y,v) : "y è il godeliano di una fbf o termine di K che
contiene occorrenze libere della variabile con godeliano v"
Cioè la sostituzione nella fbf o termine con godeliano y di
una certa variabile differente dalla variabile con godeliano v per tutte le
occorrenze libere della variabile con godeliano v produce una espressione
differente.
▸ Ff(u,v,w) : "u è il godeliano di un termine che è
libero per la variabile con godeliano v nella fbf con godeliano w"
▸ Ax1(x) : "x è il godeliano di una istanza dello
schema di assiomi seguente: B ➙ (C ➙ B)"
Si tratta del primo degli assiomi logici del calcolo del
primo ordine indicati in Mendelson, Introduction
to Mathematical Logic p. 69
▸ Ax2(x) : "x è il godeliano
di una istanza dell'assioma seguente: ((B ➙ (C ➙ D)) ➙ ((B ➙ C) ➙ (B ➙ D)))"
Si tratta del secondo degli assiomi logici del calcolo del
primo ordine indicati in Mendelson, Op.
cit. p. 69
▸ Ax3(x) : "x è il godeliano
di una istanza dell'assioma seguente: (((∼C) ➙ (∼B)) ➙ (((∼C) ➙ B) ➙ C))"
Si tratta del terzo degli assiomi logici del calcolo del
primo ordine indicati in Mendelson, Op.
cit. p. 69
▸ Ax4(x) : "x è il godeliano di una istanza
dell'assioma seguente: ∀xi B(xi) ➙ B(t)"
Si tratta del quarto degli assiomi logici del calcolo del
primo ordine indicati in Mendelson, Op.
cit. p. 69. Vedi ivi le condizioni di validità dell'assioma.
▸ Ax5(x) : "x è il godeliano
di una istanza dell'assioma seguente: ∀x1 (B ➙ C) ➙(B ➙ ∀x1 C)"
Si tratta del quinto degli assiomi logici del calcolo del
primo ordine indicati in Mendelson, Op.
cit. p. 69
▸ LAX(y) : "y è il godeliano di un assioma logico di K"
▸ Neg(x) : "il godeliano di (∼B) se x è il godeliano
di B"
▸ Cond(x,y) : "il godeliano di (B ➙ C) se x è il godeliano
di B e y è il godeliano di C"
▸ Clos(u) : "il
godeliano della chiusura di B se u è il godeliano di una fbf B"
◆ [1305221914]
Sia K una teoria
con un vocabolario ricorsivo primitivo (ricorsivo) e il cui linguaggio contiene
la costante individuale 0 e la lettera funzione f11 di ℒA (così tutti i
numerali sono termini di K. In particolare, K può essere S stesso). Allora le
seguenti funzioni e relazioni sono ricorsive primitive (ricorsive):
▸ Num(y) : il godeliano
dell'espressione y̅
▸ Nu(x) : "x è il
godeliano di un numerale"
▸ D(u) : il godeliano di B(u̅) se è il godeliano di una fbf B(x1)
Una
teoria K è detta teoria con un insieme di assiomi ricorsivo primitivo
(ricorsivo)
se la seguente proprietà PrAx è ricorsiva primitiva (ricorsiva):
PrAx(y) : "y è il godeliano di un assioma proprio
di K"
◆ S ha un insieme di assiomi ricorsivo primitivo
◆ [1305221915]
Sia K una teoria
con un vocabolario ricorsivo primitivo (ricorsivo) e un insieme di assiomi
(axiom set) ricorsivo primitivo (ricorsivo). Allora le seguenti tre relazioni
sono ricorsive primitive (ricorsive):
▸ Ax(y) : "y è il
godeliano di un assioma di K"
LAX(y) ∨ PrAx(y)
▸ Prf(y) : "y è il
godeliano di una prova in K"
▸ Pf(y,x) : "y è il
godeliano di una prova in K della fbr con godeliano x"
◆ Sia K una teoria con identità il cui linguaggio contiene la costante
individuale 0 e la lettera funzione f11 e tale che K ha
un vocabolario ricorsivo primitivo (o ricorsivo) e un insieme di assiomi
ricorsivo primitivo (o ricorsivo). Valga anche la seguente proprietà:
Per due qualsiasi numeri naturali r,s se ⊦K r̅ = s̅,
allora r = s
Allora una
qualsiasi funzione f(x1, …, xn) che è rappresentabile in
K è ricorsiva.
◆ [1305221646]
Sia K una teoria
il cui linguaggio contiene la lettera predicato "=", la costante
individuale 0 e la lettera funzione f11.
(a) Se K soddisfa la [1305221645]
allora è coerente
(b) Se K è non-coerente,
allora ogni funzione numerica è rappresentabile in K
(c) Se K è coerente e la
relazione "=" (identità) è esprimibile in K, allora K soddisfa la Si
supponga che S sia coerente. Allora la classe di funzioni ricorsive si
identifica con la classe delle funzioni rappresentabili in S.
◆ Una relazione numerica R(x1, …, xn) è
ricorsiva se e soltanto se è esprimibile in S
Si
consideri la teoria nel linguaggio ℒA con la seguente
lista finita di assiomi propri:
▸ x1 = x1
▸ x1 = x2 ➙ x2 = x1
▸ x1 = x2 ➙ (x2 = x3 ➙ x1 = x3)
▸ x1 = x2 ➙ x1' = x2' (dove x'
è il successore di x')
▸ x1 = x2 ➙ (x1 + x3 = x2
+ x3 & x3 + x1 = x3 + x2)
▸ x1 = x2 ➙ (x1 ⋅ x3 = x2 ⋅ x3 & x3 ⋅ x1 = x3 ⋅ x2)
▸ x1' = x2' ➙ x1 = x2
▸ 0 ≠ x1'
▸ x1 ≠ 0 ➙ ∃x2 (x1 = x2')
▸ x1 + 0 = x1
▸ x1 + x2' = (x1 + x2)'
▸ x1 ⋅ 0 = 0
▸ x1 ⋅ x2' =
(x1 ⋅ x2) + x1
▸ (x2 = x1 ⋅
x3 + x4 & x4 < x1 & x2
= x1 ⋅ x5 +
x6 & x6 < x1) ➙ x4 =
x6
Chiameremo
questa teoria teoria RR.
Chiaramente RR è una subteoria di S, dal
momento che tutti gli assiomi di RR sono teoremi di S. Inoltre (vedi corollario
più sotto) RR è una teoria con identità. Si noti infine che RR ha solo un
numero finito di assiomi propri. Sono provabili i seguenti teoremi:
◆ RR è una teoria con identità
◆ [1305221634]
Tutte le funzioni
ricorsive sono rappresentabili in RR
◆ In base alla [1305221634] tutte le funzioni ricorsive sono
rappresentabili in ogni estensione di RR. Pertanto, per la [1305221637] e la [1305221646(c)]
in ogni estensione coerente di RR nel linguaggio ℒA che ha un insieme di assiomi ricorsivo la classe delle funzioni
rappresentabili è identica alla classe delle funzioni ricorsive. Inoltre, per
la [1305221653]
le relazioni esprimibili in tale teoria sono le relazioni ricorsive.
◆ RR è una subteoria propria di S
IL TEOREMA DEL PUNTO FISSO. IL TEOREMA DI
INCOMPLETEZZA DI GÖDEL
Se K è
una teoria nel linguaggio ℒA, ricordi che la funzione diagonale D ha la proprietà
che, se u è il godeliano di una fbf B(x1), allora D(u) è il
godeliano della fbf B(u̅).
Quando C
è una espressione di una teoria e il godeliano di C è q, denoteremo il numerale
q̅ con ⌈C⌉. Possiamo
pensare ⌈C⌉ come il
"nome" di C nel linguaggio ℒA.
◆ Si supponga che la funzione diagonale D sia rappresentabile in una
teoria con identità K nel linguaggio ℒA. Allora, per
ogni fbf ℰ(x1) nella quale x1 è l'unica
variabile libera, esiste una fbf chiusa C tale che
⊦K C ⇔ ℰ(⌈C⌉)
◆ (Teorema del punto fisso)
Si assuma che tutte le funzioni ricorsive siano rappresentabili in una teoria
con identità K nel linguaggio ℒA. Allora, per ogni fbf ℰ(x1)
nella quale x1 è l'unica variabile libera, esiste una fbf chiusa C
tale che
⊦K C ⇔ ℰ(⌈C⌉)
Si tenga
presente che i termini "teorema del punto fisso" e "lemma della
diagonalizzazione" sono spesso usati in modo intercambiabile in altre esposizioni.
Sia K una
teoria il cui linguaggio contiene la costante individuale 0 e la lettera
funzione f11. Allora K è detta ω-coerente se, per ogni fbf B(x) di K contenente x come unica
variabile libera, se ⊦K ∼B(n̅)
per ogni numero naturale n, allora non si dà il caso che ⊦K ∃x B(x)
Sia K una
teoria nel linguaggio ℒA. K è detta una teoria
vera se tutti gli assiomi propri di K sono veri nel modello standard. Dal
momento che tutti gli assiomi logici sono veri in tutti i modelli e MP e Gen
conducono da fbf vere in un modello a fbf vere in quel modello, tutti i teoremi
di una teoria vera sono veri nel modello standard.
◆ Una qualsiasi
teoria K deve essere ω-coerente.
◆ Se K è ω-coerente, allora è coerente. L'inverso
non è vero
Un enunciato indecidibile di una teoria K
è una fbf chiusa B di K tale che né B né ∼B sono teoremi di K; in altre parole,
tale che (non-⊦k B) e (non-⊦k ∼B)
◆ (Teorema
di incompletezza di Gödel) Sia K una teoria con identità nel linguaggio ℒA che soddisfa le
seguenti tre condizioni:
(1) K
ha un set di assiomi ricorsivo (cioè PrAx(y) è ricorsivo)
(2) ⊦K 0 ≠ 1̅
(3) Ogni funzione ricorsiva è rappresentabile in
K
Per l'assunto (1) sono applicabili le proposizioni [1305221913],
[1305221914], [1305221915].
Per gli assunti (2) e (3) e il teorema [1305221653] ogni
relazione ricorsiva è esprimibile in K.
Per l'assunto (3) è applicabile il teorema del punto fisso.
Si noti che K potrebbe essere RR, S o una qualsiasi
estensione di RR che ha un set di assiomi ricorsivo.
Si ricordi
che Pf(y,x)
significa che y è il godeliano di una prova in K di una fbf con godeliano x.
Per il
teorema [1305221915], Pf è ricorsiva. Dunque Pf è esprimibile in K per mezzo di
una fbf
Pf(x2,x1).
Sia ℰ(x1)
la fbf:
(∀x2) ∼Pf(x2,x1)
Per il
teorema del punto fisso, ci deve essere una fbf chiusa G tale che:
[1305221928] ⊦K G ⇔ (∀x2) ∼Pf(x2,⌈G⌉)
In termini dell'interpretazione standard, la formula (∀x2) ∼Pf(x2,⌈G⌉) dice che non
c'è un numero naturale che sia il godeliano di una prova in K della fbf G,
che equivale ad asserire che non c'è alcuna prova in K di G. Dunque, G
è equivalente in K ad una asserzione che
G
non è provabile in K. In altre parole, G dice "Io non sono provabile
in K". E' un analogo del paradosso del mentitore: "Io sto
mentendo" (cioè "Questa asserzione non è vera"). Comunque,
sebbene il paradosso del mantitore conduce ad una contraddizoine, Gödel mostrò
che G
è una proposizione indecidibile di K. Ci riferiremo a G come alla proposizione di Gödel per K.
Dati gli assunti (1)-(3) si ha:
(a) Se
K è coerente, non-⊦K G
(b) Se
K è ω-coerente, G è una proposizione indecidibile di
K
La prova è riportata in Mendelson, Op. cit., p. 207
Il teorema di incompletezza di Gödel vale per qualsiasi
teoria con identità K nel linguaggio ℒA che soddisfa le
condizioni (1)-(3).
Si assuma che K
soddisfa anche la condizione:
[1305221945] K è
una teoria vera
(in particolare K
potrebbe essere S o una qualsiasi sottoteoria di S). Allora il teorema di
incompletezza nella parte (a) afferma che, se K è coerente, G
non è provabile in K. Ma, secondo l'interpretazione standard, G
asserisce la sua propria non-provabilità in K. Dunque, G è vero per
l'interpretazione standard.
Perdipiù, quando
K è una teoria vera, può essere formulata la seguente argomentazione intuitiva
che dimostra l'indecidibilità di G in K:
(i) Supponiamo
che ⊦K G. Dal momento che ⊦K G ⇔ (∀x2) ∼Pf(x2,⌈G⌉) segue che ⊦K (∀x2) ∼Pf(x2,⌈G⌉). Dal momento
che K è una teoria vera, (∀x2) ∼Pf(x2,⌈G⌉) è vero per
l'interpretazione standard. Ma questa fbf dice che G non è provabile in K,
contraddicendo la assunzione originale. Dunque non-⊦K G
(ii) Supponiamo
⊦K G. Dal momento che ⊦K G ⇔ (∀x2) ∼Pf(x2,⌈G⌉), segue che ⊦K (∀x2) ∼Pf(x2,⌈G⌉). Così, ⊦K (∃x2) Pf(x2,⌈G⌉). Dal momento che K è una teoria vera, questa fbf è vera
per l'interpretazione standard, cioè G è provabile in K. Questo
contraddice il risultato (i). Dunque, non-⊦K ∼G.
La prova della indecidibilità di
una proposizione di Gödel G richiedeva l'assunzione della ω-coerenza. Rosser
ha provato che, al prezzo di un lieve incremento della complessità della proposizione
indecidibile l'assunto dell'ω-coerenza può essere sostituito da quello
della coerenza.
Come in precedenza, sia K una
teoria con identità nel linguaggio ℒA che soddisfa le
condizioni (1)-(3) del teorema di incompletezza di Godel. Si assuma in aggiunta
che:
(4) ⊦K x ≤ n̅ ➙
x = 0 ∨ x = 1̅ ∨ … ∨ x = n̅ per ogni numero naturale n
(5) ⊦K x ≤ n̅
∨ n̅ ≤ x per ogni numero naturale n
Così K
può essere una qualsiasi estensione di RR con un set di assiomi ricorsivi. In
particolare, K può essere RR o S.
Si ricordi che, per la proposizione [1305221913],
Neg è una funzione ricorsiva
primitiva tale che, se x è il godeliano di una fbf B, allora Neg(x) è il godeliano di (∼B).
Dal momento che tutte le funzioni
ricorsive sono rappresentabili in K, sia Neg(x1,
x2) una fbf che rappresenti Neg
in K. Si costruisca la seguente fbf ℰ(x1):
(∀x2)
(Pf(x2,x1)
➙ (∀x3)
(Neg(x1,x2)
➙ (∃x4)
(x4 ≤ x2 & Pf(x4,x3))))
Per il teorema del punto fisso, c'è una
fbf chiusa R tale che
[1305221015] ⊦K R ⇔ ℰ(⌈R⌉)
R è chiamata la proposizione di Rosser per K. Il
significato intuitivo di R è che nell'interpretazione
standard R asserisce che, se R ha una prova in K, diciamo con
godeliano x2, allora ∼R ha una prova in K con godeliano inferiore a x2.
Questa è una maniera indiretta da parte di R di asserire la propria
non-provabilità sotto l'assunzione della coerenza di K. Questo è espresso nel
seguente
◆ (Teorema
di Godel-Rosser) Si supponga che K soddisfi le condizioni (1)-(5). Se K è coerente
allora R è una proposizione indecidibile di K.
La prova è in Mendelson, Op.
cit. p. 209
La proposizione di Gödel e la
proposizione di Rosser per la teoria S sono proposizioni indecidibili di S. Esse
hanno un certo significato intuitivo metamatematico. Per esempio, una
proposizione G di Gödel asserisce che G non è provabile in S. Fino a tempi
recenti, non erano note proposizioni indecidibili di S che avessero una
intrinseca natura matematica. Ma nel 1977 Kirby, Paris e Harrington hanno trovato
una proposizione indecidibile di significato matematico di calcolo combinatorio
collegata al cosiddetto teorema finito di Ramsey.
Una teoria K è detta una teoria ricorsivamente assiomatizzabile
se c'è una teoria K* che ha gli stessi teoremi di M e tale che K* ha un set di
assiomi ricorsivo.
◆ [1305222107] Sia K
una teoria nel linguaggio ℒA. Se K è una estensione di RR ricorsivamente
assiomatizzabile e coerente, allora K ha una proposizione indecidibile.
Un insieme effettivamente decidibile di
oggetti è un insieme per cui esiste una procedura meccanica che determina,
per ogni dato oggetto, se quell'oggetto appartiene o no all'insieme. Per procedura meccanica intendiamo una procedura che è attuata
automaticamente senza nessun bisogno di originalità o ingegnosità nella sua
applicazione. D'altro lato, un insieme A di numeri naturali è detto essere un insieme ricorsivo se la proprietà x ∈ A è ricorsiva. La precisa nozione di insieme
ricorsivo corrisponde alla idea intuitiva di un insieme effettivamente decidibile
di numeri naturali. Questa ipotesi è conosciuta come Tesi di Church.
Si
ricordi che una teoria è detta assiomatica se il suo set di assiomi è effettivamente
decidibile. Chiaramente, il set di assiomi è effettivamente decidibile se e
soltanto se il set dei numeri di Gödel degli assiomi è effettivamente
decidibile (dal momento che possiamo passare effettivamente da una fbf al suo
numero di Gödel e inversamente, dal numero di Gödel alla fbf). Dunque, se
accettiamo la tesi di Church, dire che K ha un set ricorsivo di assiomi è
equivalente a dire che K è una teoria assiomatica e dunque, la proposizione mostra che RR è essenzialmente
incompleta, cioè, che ogni estensione assiomatica coerente di RR ha una
proposizione indecidibile. Questo risultato è veramente indesiderabile; ci dice
che non esiste alcuna assiomatizzazione completa dell'aritmetica, cioè non
esiste un modo di creare un sistema assiomatico sulla base del quale possiamo
risolvere tutti i problemi della teoria dei numeri.
◆ La tesi di Church è equivalente
all'affermazione che una funzione numerica è effettivamente computabile se e
soltanto se è ricorsiva.
Sia K una estensione di S nel
linguaggio ℒA tale che K ha un
set ricorsivo di assiomi. Sia ConK la seguente fbf
chiusa di K:
(∀x1)(∀x2)(∀x3)(∀x4) ∼(Pf(x1,x2)
& Pf(x2,x4) & Neg(x3,x4))
Per
l'interpretazione standard, ConK asserisce che non ci
sono prove in K di una fbf e della sua negazione, cioè che K è coerente. Si
consideri la seguente proposizione:
[1305222117] ConK ➙ G
dove G
è una proposizione di Gödel per K. Si ricordi che G asserisce che G
non è provabile in K. Dunque asserisce che, se K è coerente, allora G
non è provabile in K. Ma questa è proprio la prima metà del teorema di
incompletezza di Gödel. Il ragionamento metamatematico utilizzato nella prova
di quel teorema può essere espresso e
sviluppato entro K stesso, cosicché si ottiene una prova in K di Nella loro prova del secondo teorema di Gödel, Hilbert e Bernays basarono il loro lavoro su tre
cosiddette condizioni di derivabilità.
Per amor di precisione ci limiteremo qui alla teoria S, sebbene tutto ciò che
diremo vale per le estensioni ricorsivamente assiomatizzabili di S.
Per formulare i risultati di
Hilbert-Bernays, sia Bew(x1) un simbolo che
sta per la formula
(∃x2) Pf(x2,x1)
Così,
nell'interpretazione standard, Bew(x1) significa che c'è
una prova in S della fbf con numero di Gödel x1; cioè, la fbf con
godeliano x1 è provabile in S. Si noti che una proposizione di Gödel
G per S soddisfa la condizione del punto fisso:
⊦S G ⇔ Bew(⌈G⌉)
Le condizioni di derivabilità di
Hilbert-Bernays sono:
(HB1) Se ⊦S C allora ⊦S Bew(⌈C⌉)
(HB2) ⊦S Bew(⌈C ➙ D⌉) ➙ (Bew(⌈C⌉) ➙ Bew(⌈D⌉))
(HB3) ⊦S Bew(⌈C⌉) ➙ Bew(⌈Bew(⌈C⌉)⌉)
dove C e D sono fbf chiuse
arbitrarie di S. (HB1) è immediata e (HB2) è una facile conseguenza delle proprietà di Pf. La prova di (HB3) è difficile e sottile e
viene qui omessa.
Una proposizione di Gödel G
per S asserisce la propria non-provabilità in S:
⊦S G ⇔ ∼Bew(⌈G⌉)
Possiamo applicare il teorema del
punto fisso per ottenere una proposizione H tale che
⊦S H ⇔ Bew(⌈H⌉)
H è chiamata la proposizione di Henkin per S. H
asserisce la propria provabilità in S.
Chiediamoci se H sia provabile,
non-provabile o indecidibile in S.
Scriviamo ☐C per Bew(⌈C⌉), dove C è una qualsiasi
fbf. Riscriviamo le condizioni di Hilbert-Bernays:
(HB1) Se ⊦S C allora ⊦S ☐C
(HB2) ⊦S ☐(C ➙ D) ➙ (☐(C)
➙ ☐(D))
(HB3) ⊦S ☐(C)
➙ ☐☐(C)
La proposizione di Gödel e la
proposizione di Henkin soddisfano le equivalenze:
⊦S G ⇔ ∼☐G
⊦S H ⇔ ∼☐H
◆ (Teorema
di Löb) Sia C una proposizione di S. Se ⊦S ☐C ➙ C, allora ⊦S C
◆ Sia H una proposizione di Henkin per S.
Allora ⊦S H e H è vera per l'interpretazione standard
Il
teorema di Löb ci mette in grado di provare il
secondo teorema di Godel.
◆ (Secondo Teorema di Godel)
Se S è coerente, allora non-⊦S ConsS
INDECIDIBILITA' RICORSIVA. TEOREMA DI CHURCH.
Se K è una teoria, sia TK il set dei godeliani dei
teoremi di K.
K è detta una teoria ricorsivamente decidibile se TK è un set
ricorsivo (cioè la proprietà x ∈ TK è ricorsiva). K è detta una teoria ricorsivamente indecidibile se K
e tutte le estensioni consistenti di K sono ricorsivamente indecidibili.
Se accettiamo la Tesi di Church,
allora la indecidibilità ricorsiva equivale alla indecidibilità effettiva, cioè
alla non-esistenza di una procedura decisionale meccanica per testare la
proprietà di essere un teorema. La non esistenza di una simile procedura
meccanica significa che è richiesta ingegnosità per determinare se arbitrarie
fbf sono teoremi.
◆ Sia K una teoria coerente con identità nel linguaggio ℒA in cui la
funzione diagonale D è rappresentabile. Allora la proprietà x ∈ TK non è
esprimibile in K
Un
insieme B di numeri naturali è detto insieme
aritmetico se c'è una fbf B(x) nel linguaggio ℒA con una
variabile libera x, tale che, per ogni numero naturale n, n ∈ B se e soltanto se B(n̅) è vero nell'interpretazione
standard.
◆ (Teorema di Tarski) Sia Tr l'insieme dei numeri di Gödel di fbf di S che sono vere
per l'interpretazione standard. Allora Tr
non è aritmetico.
◆ Sia K una teoria coerente con identità nel linguaggio ℒA in cui tutte le
funzioni ricorsive sono rappresentabili. Si assuma anche che ⊦K 0 ≠ 1. Allora K è ricorsivamente indecidibile.
◆ RR è essenzialmente ricorsivamente indecidibile
◆ Sia K una teoria con un vocabolario ricorsivo.
Se K è ricorsivamente assiomatizzabile e ricorsivamente indecidibile, allora K
è una teoria incompleta (cioè ha una
proposizione indecidibile).
◆ (Teorema
di Godel-Rosser) Ogni estensione coerente e ricorsivamente assiomatizzabile
di RR ha una proposizione indecidibile
Siano K1 e K2
due teorie nello stesso linguaggio. K2 è chiamata una estensione finita di K1 se e
soltanto se c'è un insieme A di fbf e un insieme finito B di fbf tali che:
▸ i teoremi di K1 sono precisamente le fbf
derivabili da A;
▸ i teoremi di K2 sono
precisamente le fbf derivabili da A ∪ B.
Denoti K1
∪ K2 la teoria
il cui set di assiomi è l'unione del set di assiomi di K1 e di
quello di K2. Diciamo che K1 e K2 sono teorie compatibili se K1 ∪ K2 è coerente.
◆ Siano K1 e K2 due teorie
nello stesso linguaggio. Se K2 è una estensione finita diK1
e se K2 è ricorsivamente indecidibile, allora K1 è
ricorsivamente indecidibile.
◆ Sia K una teoria nel linguaggio ℒA. Se K è
compatibile con RR, allora K è ricorsivamente indecidibile.
◆ Ogni teoria vera K è ricorsivamente
indecidibile
◆ Sia PS il calcolo predicativo nel
linguaggio ℒA. Allora PS
è ricorsivamente indecidibile
Con PF intendiamo il pieno calcolo predicativo del primo ordine, contenente tutte le
lettere predicato, le lettere funzione e le costanti individuali. Sia PP il puro calcolo predicativo del primo ordine, contenente tutte le
lettere predicative ma non lettere funzione o costanti individuali.
◆ C'è una funzione ricorsiva h tale che, per ogni
fbf B di PF con godeliano u, c'è una fbf B' di PP con godeliano h(u) tale che B
è provabile in PF se e soltanto se B' è provabile in PP.
◆ PF e PP sono ricorsivamente indecidibili.