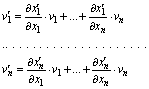[1309152356] ß PERCORSI

▸ limite, ordinale: [Go 209] Gli ordinali possono essere ben ordinati da ∈, che è un ordine stretto lineare ([Go 165, 207]). In un ordine stretto lineare vengono definiti i punti-limite nel seguente modo ([Go 169]): l'elemento c di X è un punto limite dell'insieme ordinato se c'è un elemento x di X con x < c, e per ogni elemento x ∈ X con x < c c'è qualche y ∈ X con x < y e y < c. Un ordinale limite non è altro che un punto limite nel buon ordine della classe degli ordinali.

▸ lineare, ordine (stretto o debole): [Go 164,165] Dati a,b, si ha a R b oppure b R a oppure a = b

▸ non-contabile, insieme: [Go 148] an infinite set which is not countable is said to be uncountable or uncountably infinite

▸ ordine lineare stretto: [Go 165] E' un ordine irriflessivo, transitivo e tale che dati a,b si ha a < b oppure a > b oppure a = b

▸ ordine lineare debole: [Go 164] E' un ordine riflessivo, transitivo, antisimmetrico e lineare (dati a,b, si ha a ≤ b oppure b ≤ a oppure a = b)

▸ ordine parziale stretto: [Go 165] E' un ordine riflessivo, transitivo ma non lineare (i.e. dati a,b, si ha a ≤ b oppure b ≤ a oppure a = b)

▸ somma generalizzata di cardinali: [Lo 162] Se {k_i}_i_∈_I è un insieme di cardinali, I un insieme anche infinito, la somma ∑_I k_i è definita come la cardinalità dell'insieme ∪{a_i | i ∈ I} dove {a_i}_i_∈_I è un insieme di insiemi due a due disgiunti aventi ciascuno la cardinalità corrispondente k_i. Non è richiesto che i k_i siano distinti; se ad esempio k_i = 1 per ogni i ∈ k, allora ∑_k 1 = k. Se k_i = k per ogni i ∈ I, allora ∑_i k_i = Card(Ixk); infatti per ogni i ∈ I gli insiemi {<i,α> | α ∈ k} hanno la stessa cardinalità k, sono disgiunti per indici i diversi e I x k è l'unione di questi insiemi

▸ successore, cardinale: [Lo 158] Dato l'ordine tra cardinali definito da ∈, h⁺ indica il primo cardinale maggiore di h, che è detto cardinale successore (per il concetto di maggiore vedi la trattazione dell'ordine tra cardinali, con riguardo alla esposizione di Lolli).

▸ successore, ordinale: [Go 209] Gli ordinali possono essere ben ordinati da ∈, che è un ordine lineare stretto ([Go 165,207]). In un ordine lineare stretto vengono definiti i punti successori ([Go 170]): siano x, c, elementi di X. Allora c è il successore di X se x < c e per tutti gli y, se x < y allora c = y oppure c < y. Un ordinale successore è un punto successore nel buon ordine della classe degli ordinali.

▸ transitivo, insieme : Un insieme S è detto transitivo se e solo se ogni membro di un membro di S è esso stesso un membro di S.

Condizioni equivalenti:

∪S ⊆ S

a ∈ S ➙ a ⊆ S

S ⊆ P(S)

simboli

back to index

A ≼ B

C'è una funzione iniettiva A ➙ B, che potrebbe anche essere bijettiva

A ≺ B

C'è una funzione iniettiva ma non bijettiva A ➙ B, cioè A ≼ B ma A ≉ B (A non è equinumeroso con B)

α ⊕ β

[Go 219] somma tra ordinali:

α ⊕ 0 = 0

α ⊕ β⁺ = (α ⊕ β)⁺

α ⊕ β 0 ∪{α ⊕ λ | λ ∈ β} per un ordinale limite β

nozioni di teoria degli insiemi

notizie storiche sulla teoria degli insiemi

back to index

La teoria degli insiemi come oggetti astratti, studiati per le loro proprietà intrinseche, nacque in gran parte ad opera del matematico tedesco Georg Cantor (1845-1918). I suoi lavori sull'argomento apparvero nel periodo 1874-1897.

Cantor nel 1871 si rese conto che l'operazione di formare l'insieme dei punti limite di insiemi geometrici di punti può essere ripetuta un numero non-finito di volte.

Nel dicembre del 1873 Cantor provò che l'insieme dei numeri reali non può essere posto in corrispondenza biunivoca con quello degli interi. Questo risultato fu pubblicato nel 1874. Nel 1879 e negli anni successivi Cantor pubblicò una serie di lavori incentrati sui concetti generali di insieme astratto e di "numeri transfiniti".

Il lavoro di Cantor fu accolto con favore da alcuni dei maggiori matematici del tempo, come Dedekind e Hilbert. Altri, come Kronecker, attaccarono il concetto di infinito attuale.

[En 14] Verso la fine dell'800 fu fatto uno sforzo per presentare i principi della teoria degli insiemi come principi di logica, leggi autoevidenti del pensiero deduttivo. Il principale lavoro fu quello del matematico e logico tedesco Gottlob Frege. Nel 1893 e nel 1903 pubblicò un lavoro in due volumi in cui si proponeva di dimostrare che la matematica può venir dedotta da principi logici. Ma poco prima della pubblicazione del secondo volume, Bertrand Russell informò Frege di una contraddizione derivabile dal suo sistema (il cosiddetto paradosso di Russell, che fu notato indipendentemente da Ernst Zermelo).

[En 14] Nel 1897 Cesare Burali-Forti scoprì l'omonimo paradosso sugli ordinali.

[En 14] La prima assiomatizzazione della teoria degli insiemi fu pubblicata da Ernst Zermelo nel 1908. Il suo Aussonderungsaxiom aveva qualche imprecisione che fu emendata da Thoralf Skolem e altri.

[En 14] Nel 1922 Abraham Fraenkel e altri proposero di aggiungere l'assioma di rimpiazzamento. La lista di assiomi così arricchita prende il nome di "assiomi ZF" o "teoria ZF" o "sistema ZF".

[En 14] L'assioma di regolarità o fondazione, implicitamente stabilito in un lavoro di Dmitry Mirimanoff del 1917 e fu aggiunto da von Neumann nel 1925.

[En 14] Nel 1925 von Neumann propose un sistema di assiomi che ammetteva classi proprie come oggetti legittimi. Paul Bernays migliorò il sistema di von Neumann in una serie di lavori del 1937 e degli anni successivi. Kurt Gödel utilizzò tale sistema, modificato, in una sua monografia del 1940. Il sistema che alla fine ne risultò è noto come "sistema NBG" o "teoria NBG".

la vita dei matematici

back to index

Come cominciò l'avventura di Cantor con i numeri infiniti? Per puro caso. Ad un certo punto della sua vita un matematico si imbatte in un problema che per lui riveste uno straordinario fascino, vi scorge ciò che gli altri non sono in grado di scorgere. A quel punto, la sua strada è tracciata.

Evariste Galois era affascinato dal problema delle equazioni algebriche di grado superiore al terzo. Augustin Louis Cauchy studiò per tutta la vita la definizione di limite. Ne era così preso che quando il giovanissimo genio danese Niels Henrik Abel gli inviò i suoi lavori sulle equazioni, non ebbe il tempo di leggerli. Abel morì disperato a ventisei anni, due giorni prima di ricevere la nomina a professore all'università di Berlino, che avrebbe potuto ottenere molto prima, se Cauchy avesse gettato uno sguardo sul suo lavoro.

Così è la mente di un matematico. Riemann studiò l'elettromagnetismo e i numeri complessi, ma dedicò gli sforzi più grandi ad elaborare il concetto di varietà, che portò frutto solo settant'anni dopo la sua morte. Gregorio Ricci Curbastro e il suo brillante allievo, Tullio Levi-Civita, furono affascinati dalla bellezza dei tensori⁽¹⁾ e ne esposero le leggi, incuranti del fatto che molti all'epoca li giudicassero null'altro che sterile formalismo.

Vent'anni più tardi Albert Einstein, che aveva utilizzato il linguaggio geometrico multidimensionale di Hermann Minkowski per esporre la teoria della relatività speciale, ed era alla ricerca di un simbolismo più adeguato per la sua teoria della relatività generale, si imbatté nei lavori dei due italiani e, trovandoli straordinariamente difficili, se li fece spiegare dall'amico Marcel Grossmann. La descrizione del modo in cui la gravità incurva lo spazio fu scritta nel linguaggio dei tensori. E' una delle ragioni per cui viene considerata una delle più belle creazioni dell'ingegno umano.

Alcuni matematici si cimentano con problemi troppo difficili per le conoscenze del loro tempo, sono destinati all'amarezza del fallimento. L'ultimo teorema di Fermat tra gli altri, con la sua ingannevole semplicità, ha attirato gli studiosi come la luce attira le falene, ma è tutt'oggi indimostrato.

Cantor, al confronto, è stato eccezionalmente fortunato. I problemi che studiò cominciavano appena allora ad essere sollevati nei lavori degli analisti più valenti, da Weierstrass a Bolzano a Dirichlet. Non aveva punti di riferimento, ma nondimeno, le conoscenze della sua epoca erano mature per le sue scoperte.

biografia di georg cantor

back to index

Cantor fu uno dei matematici più geniali del XIX secolo. Al di fuori della cerchia dei matematici, il suo nome viene fatto unicamente in connessione con la "teoria degli infiniti". In realtà i suoi contributi furono straordinari e molteplici.

Cantor iniziò la teoria degli insiemi, quella degli infiniti e quella degli insiemi di punti. La sua definizione di punto limite e di insieme derivato diede origine ad una classificazione dei punti di un insieme del tutto nuova e alternativa a quella semplice di appartenenza-non appartenenza. Felix Hausdorff nel suo Grundzüge der Mengenlehre (I fondamenti della teoria degli insiemi) del 1914 sviluppò questa classificazione e sulla base di essa diede vita ad una nuova disciplina, la topologia⁽¹²⁾, destinata ad avere una importanza fondamentale fino ai giorni nostri.

Lo studio delle relazioni tra punti, che aveva consentito a Cantor di proporre la sua definizione condussero Hausdorff a quella di punto interno, punto esterno, punto di confine, punto di accumulazione⁽¹³⁾, che sono alla base di questa disciplina, anche se raramente il nome di Cantor viene accostato alla sua nascita.

Ma oltre a quelli più innovativi, Cantor dette contributi notevoli anche nelle aree più tradizionali della matematica, quando se ne occupò (come ad esempio nei lavori sulla serie di Fourier). Di qualsiasi cosa si interessasse otteneva invariabilmente risultati originali e profondi.

Georg Cantor (1845-1918) nacque in Russia da una famiglia di ebrei danesi che si trasferì poi in Germania poco dopo la sua nascita. Il padre lo spinse a studiare ingegneria ed egli si iscrisse nel 1863 all'università di Berlino con questa intenzione, ma, caduto sotto l'influenza di Weierstrass, passò ben presto alla matematica pura. Nel 1869 diventò Privatdozent a Halle e nel 1879 fu promosso professore. Quando aveva ventun anni pubblicò nel "Journal für Mathematik" il suo primo lavoro rivoluzionario sulla teoria degli insiemi infiniti. Benché alcune delle sue proposizioni fossero considerate false dai matematici più anziani, la sua grande originalità e brillantezza attirarono l'attenzione di tutti. In seguito continuò a pubblicare lavori sulla teoria degli insiemi e sui numeri transfiniti fino al 1897.

Non ci si poteva certo aspettare che l'opera di Cantor, che risolse problemi vecchi di secoli e che rivoltò completamente molte precedenti credenze, venisse accettata immediatamente. Le sue idee sui numeri cardinali e ordinali transfiniti suscitarono l'ostilità del potente Leopold Kronecker, che attaccò selvaggiamente le idee di Cantor per oltre un decennio. Ad un certo momento Cantor ebbe un esaurimento nervoso, ma nel 1887 riprese a lavorare. Tuttavia, anche se Kronecker morì nel 1891, i suoi attacchi lasciarono i matematici sospettosi circa i risultati di Cantor.

La teoria degli insiemi come oggetti astratti, studiati per le loro proprietà intrinseche, nacque in gran parte ad opera di Cantor. I suoi lavori sull'argomento apparvero nel periodo 1874-1897.

La teoria cantoriana degli insiemi è sparsa in molti lavori. I suoi concetti e teoremi sono contenuti nei "Mathematische Annalen" e nel "Journal für Mathematik" a partire dal 1874.

La teoria cantoriana degli insiemi costituì un audace passo innanzi in un campo che era stato preso intermittentemente in considerazione fin dal tempo dei Greci. Essa richiedeva l'applicazione rigorosa di ragionamenti puramente razionali e affermava l'esistenza di insiemi infiniti di potenza sempre maggiore che sono del tutto al di fuori delle capacità di comprensione della intuizione umana. Sarebbe stato davvero strano se queste idee, molto più rivoluzionarie della maggior parte di quelle introdotte in precedenza, non avessero incontrato opposizione.

I dubbi circa la fondatezza di questa teoria furono rinforzati da alcuni problemi sollevati dallo stesso Cantor e da altri. In due lettere a Dedekind del 28 luglio e del 28 agosto 1899, Cantor si chiese se l'insieme di tutti i numeri cardinali sia esso stesso un insieme perché, se lo fosse, avrebbe dovuto avere un numero cardinale maggiore di ogni altro numero cardinale. Egli pensava di dover rispondere in senso negativo distinguendo tra insiemi coerenti e insiemi non coerenti. In seguito, nel 1897, Cesare Burali-Forti osservò che la successione di tutti i numeri ordinali, che è bene ordinata, dovrebbe avere come numero ordinale il più grande di tutti i numeri ordinali (questa difficoltà era già stata notata da Cantor nel 1895). Questi e altri problemi non risolti, chiamati paradossi, incominciarono a essere notati alla fine dell'Ottocento.

Come conseguenza, l'opposizione si fece essa stessa più dura. Kronecker, come si è già osservato, attaccò il concetto di infinito attuale e si oppose alle idee di Cantor quasi fin dall'inizio. Felix Klein non era affatto tenero con esse. Henri Poincaré osservò criticamente: "E' però accaduto che abbiamo incontrato certi paradossi, certe apparenti contraddizioni che sarebbero piaciute a Zenone di Elea e alla Scuola di Megara… Per parte mia io penso, e non sono il solo, che il punto importante sta nel non introdurre mai oggetti che non possono essere definiti completamente con un numero finito di parole". In seguito si riferisce alla teoria degli insiemi come a un interessante "caso patologico". Predisse anche (nello stesso articolo) che "le generazioni che verranno considereranno la Mengenlehre di Cantor come una malattia da cui si è guariti". Hermann Weyl parlò della gerarchia cantoriana degli aleph come di "nebbia stesa sopra una nebbia".

Tuttavia, il lavoro di Cantor fu accolto con favore da alcuni dei maggiori matematici del tempo, come Dedekind e Hilbert. Molti eminenti matematici furono profondamente colpiti dalle applicazioni che la nuova teoria aveva già trovato. Nel primo Congresso internazionale dei matematici di Zurigo del 1897 Hurwitz e Hadamard indicarono importanti applicazioni della teoria dei numeri transfiniti all'analisi. Altre applicazioni vennero presto fatte nella teoria della misura e in topologia. David Hilbert diffuse in Germania le idee di Cantor e nel 1926 disse: "Nessuno riuscirà mai ad espellerci dal paradiso che Cantor ha creato per noi". Egli lodò l'aritmetica transfinita di Cantor come "il prodotto più sbalorditivo del pensiero matematico, una delle più belle realizzazioni dell'attività umana nel campo dell'intelletto puro". Bertrand Russell descrisse l'opera di Cantor come "la più grande, probabilmente, di cui il nostro tempo può vantarsi".

il lavoro sulle serie convergenti di fourier

back to index

[Go 127, 202, 244] Intorno al 1870 Cantor stava studiando le serie convergenti di Fourier⁽²⁾. Una serie convergente di Fourier è una somma di termini trigonometrici in grado di approssimare pressoché qualsiasi funzione che presenti minimi requisiti di regolarità nell'intervallo (–π, +π). La serie di Fourier, rispetto allo sviluppo di Taylor, ha il triplice vantaggio di poter approssimare anche funzioni discontinue, funzioni che non possiedono una espressione analitica e di convergere non solo nell'intorno di un punto, ma in un ampio intervallo trigonometrico. Ma l'aspetto più interessante è che una serie di Fourier è una serie infinita. Da questo, Cantor fu indotto ad occuparsi del concetto stesso di infinito.

la storia dell'infinito attuale nel pensiero matematico

back to index

A questo punto va fatta una digressione. Cantor, utilizzando insiemi con infiniti elementi, a cominciare da omega, aveva introdotto un concetto sino ad allora severamente bandito dalla matematica: l'infinito attuale.

I suoi ragionamenti andavano contro duemilacinquecento anni di pregiudizi, risalendo indietro all'antica Grecia. Il pensiero ellenico considerava in modo negativo l'infinito, l'apeiron, considerato l'antitesi di ciò che è finito, delimitato, dotato di forma. Nulla può esistere senza avere una forma. Ma essere dotato di forma vuol dire essere delimitato, avere un limite. L'infinito era l'informe, l'imperfetto, il caos, il non essere.

Già Aristotele aveva tracciato la distinzione tra infinito attuale e infinito potenziale. Gli interi positivi, ammonisce, sono potenzialmente infiniti in quanto è sempre possibile aggiungere 1 a un qualsiasi numero per ottenerne uno nuovo, ma il loro insieme infinito, in quanto tale, non esiste, perché non può essere ottenuto con questo procedimento.

Gli insiemi infiniti erano sempre stati visti con diffidenza e paura, perché generano inquietanti paradossi. Il paradosso di Zenone mostra che i greci avevano già capito che l'ipotesi dell'infinito rende problematica la descrizione del moto.

Se un punto percorre in un tempo finito una porzione di linea, il tempo impiegato a percorrere ciascun intervallo della porzione diminuisce all'aumentare del numero di intervalli in cui è frazionata la linea. Un intervallo di un ventesimo viene percorso in un tempo che è la metà di quello impiegato a percorrere un intervallo di un decimo. Se il numero dei punti della porzione è infinito, ciascun punto, essendo inesteso, viene superato in un tempo eguale a zero. Diversamente si originerebbe il paradosso di Zenone: il tempo di percorrenza sarebbe infinito. Ma questa conclusione è inaccettabile, perché la somma di infiniti zeri dà zero, e il tempo in cui verrebbe percorsa la porzione di linea sarebbe esso stesso nullo.

Proclo, il commentatore di Euclide, osserva che un diametro divide un cerchio in due metà e poiché esistono un numero infinito di diametri, devono esistere il doppio di quel numero di metà: una contraddizione che impedisce di parlare di infinità attuale di parti di un cerchio.

Gli Scolastici notarono che due cerchi concentrici hanno i punti esattamente collegati dagli infiniti raggi del cerchio maggiore, cosicché devono averne lo stesso numero di punti, ciò che tuttavia è impossibile, perché la lunghezza delle due circonferenze è diversa.

Galileo combatté contro gli infiniti e li respinse perché non erano riconducibili alla ragione. Nei Discorsi e dimostrazioni matematiche intorno a due nuove scienze osserva che i punti di due lati corrispondenti di triangoli simili possono essere posti in corrispondenza biunivoca fra loro mediante linee rette che partono dal vertice opposto, cosicché le due lunghezze contengono presumibilmente lo stesso numero di punti. Egli osserva anche che i numeri interi possono essere messi in corrispondenza biunivoca con i loro quadrati assegnando semplicemente ad ogni numero il suo quadrato. Ciò conduce a diversi "gradi" di infinito che, secondo Galileo, non possono esistere. Tutte le quantità infinite sono le stesse e non possono essere comparate egli diceva.

Persino Karl Friedrich Gauss, forse il più grande matematico puro di tutti i tempi, insignito dai contemporanei col titolo di Princeps Mathematicorum, in una lettera a Schumacher del 1831, protesta contro l'uso di una quantità infinita come quantità attuale nelle operazioni matematiche. Tutti gli studenti di liceo hanno imparato a proprie spese che non si deve mai scrivere 1/∞ = 0.

L'atteggiamento che tendeva ad evitare questi problemi spinosi era ipocrita, e io ho sempre detestato l'ipocrisia. La teoria degli insiemi, una importante branca della matematica, non poteva svilupparsi senza risolvere questi problemi, perché molti insiemi – alcuni dei più importanti, in verità – sono insiemi infiniti. Qualcuno doveva compiere il primo passo.

Già nel Seicento, con la creazione dell'analisi infinitesimale ad opera contemporaneamente ed indipendentemente di Isaac Newton e di Gottfried Wilhelm Leibniz, i paradossi dell'infinito si erano infiltrati nei ragionamenti matematici.

Consideriamo un bicchiere d'acqua di 5 cm. di diametro che abbia solo due dimensioni, in cui possiamo osservare il profilo della superficie del liquido come una linea. Supponiamo di dare un colpo al bicchiere in modo che la linea del profilo non sia più orizzontale. Supponiamo che segua un andamento ascendente da sinistra a destra, fin quasi in prossimità del bordo, secondo la funzione:

y = x²

dove y è l'altezza del liquido, e x è la distanza del punto del profilo dalla parete sinistra del bicchiere (il tutto misurato in centimetri). Vogliamo calcolare mediante l'analisi infinitesimale il volume (in realtà nel nostro caso area) del liquido.

Per ottenere una misura approssimata, suddividiamo la larghezza x del bicchiere in 5 intervalli di 1 cm. Moltiplichiamo l'estensione dell'intervallo (1 cm.) per l'altezza che ha il liquido nel punto finale dell'intervallo. Otteniamo una sommatoria del tipo seguente:

dove X maiuscolo è la larghezza del bicchiere. Se sostituiamo m a 5 come numero di intervalli arbitrario, otteniamo:

Facendo aumentare il numero degli intervalli l'accuratezza della nostra misura aumenta col valore di m: m = 5, m = 10, m = 20, ecc. Ma la stima esatta dell'area posta sotto il profilo del liquido la otteniamo solo se poniamo m = ∞ ovvero, più rigorosamente, se facciamo tendere m ad infinito:

Area sotto la linea del liquido =

In termini matematici rigorosi, il limite di cui sopra è l'integrale della funzione y = x², e cioè f(x) = x²:

Area sotto la linea del liquido =

Il valore di questo integrale o sommatoria infinita è agevolmente calcolabile una volta trovata la funzione primitiva della funzione f(x) = x²:

y = x³/3 + C

con C costante di integrazione.

La funzione primitiva di una funzione f(x) è la funzione g(x) di cui f(x) rappresenta la derivata: f(x) = D[g(x)].

Nel nostro caso f(x) = x² rappresenta la derivata della funzione g(x) = x³/3 + C.

Se x² è la derivata di x³/3 + C, questo vuol dire che x² rappresenta il limite del rapporto incrementale della funzione x³/3 + C relativo ad ogni punto del suo dominio. Pertanto, per esprimersi nei termini impropri degli infinitesimi, la differenza tra il valore della funzione f(x) = x³/3 + C in un punto x₀ + r e il valore in un punto x₀ è il limite della sommatoria dei valori delle derivate in ciascuno dei punti dell'intervallo [x₀, x₀+r] moltiplicate per l'estensione dell'intervallo infinitesimo che contiene il punto. Con simbolismo che lascia alquanto a desiderare sotto il punto di vista del rigore formale possiamo scrivere:

dove Df(x) è la derivata x² della funzione f(x) = x³/3 + C.

Si noti che la sommatoria a secondo membro è proprio l'integrale della funzione Df(x) = x²:

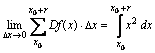
Possiamo pertanto scrivere:

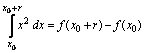
Sostituendo i valori relativi al nostro problema otteniamo:

e cioè:

In base ai calcoli, dunque, l'area del liquido nel bicchiere bidimensionale di larghezza X è pari a 41,666… cm².

A tutti gli studenti viene spiegato che il simbolo di integrazione proposto da Leibniz e oggi in uso:" ∫ ", non è altro che una deformazione dell'ordinario simbolo di sommatoria " ∑ ", a significare che la somma si riferisce non ad intervalli finiti, ma ad intervalli risultanti da una infinita suddivisione del segmento dell'asse x in riferimento al quale si vogliono sommare i valori della funzione. L'espressione tipica del calcolo integrale " ∫ f(x) dx "starebbe insomma per " ∑ f(x) ⋅ ∆x " dove invece di "∆x" si mette "dx" per indicare intervalli infinitesimi.

Questo procedimento non si concilia molto bene con l'idea, che risale ai greci, che un segmento materiale non può essere infinitamente indivisibile, idea che dette origine all'atomismo di Democrito. Di fatto, abbiamo supposto che il segmento orizzontale che rappresenta la base del bicchiere sia infinitamente divisibile e che a ciascun punto inesteso corrisponda una data altezza del liquido: come è possibile che abbiamo ottenuto un risultato che coincide con le nostre misurazioni di un oggetto materiale?

E non si pensi che le nostre misurazioni non possano essere così accurate da non rilevare discrepanze. Le formule dell'elettromagnetismo, che calcolano i valori dei campi elettromagnetici relativi ad aree e volumi, utilizzano pure esse l'analisi infinitesimale, e i risultati dei calcoli possono venir verificati con precisione altissima. Quantomeno, nessuna misurazione ha sinora contraddetto l'ipotesi dell'infinita divisibilità.

A riprova del fatto che la sommatoria su infiniti intervalli è un concetto paradossale, si può portare la storia del concetto di infinitesimo, un concetto errato che oggi viene utilizzato dagli insegnanti di matematica solo in casi disperati, per far capire ad alunni completamente refrattari ai concetti matematici la nozione di derivata.

La derivata di una funzione si ottiene considerando variazioni Δx sempre più piccole della x, a cui corrispondono variazioni Δy sempre più piccole della y. La derivata è il limite del rapporto Δy/Δx quando il valore di Δx tende a zero. Leibniz, in una lettera a Wallis del 1690, diceva che la derivata era il rapporto tra quantità infinitesime, "minori di qualsiasi quantità finita" e tuttavia non nulle. Per rimarcare questa distinzione, utilizzava, per il rapporto che costituiva la derivata il simbolo dy/dx anziché quello Δy/Δx, e chiamava dx e dy differenziali, per distinguerli dalle variazioni finite costituite da Δx e Δy. I differenziali o infinitesimi erano queste misteriose quantità che venivano concepiti come quasi inestese.

Solo la definizione e l'impiego del concetto di limite, oltre un secolo più tardi, portò finalmente chiarezza e consentì ai matematici tirare un sospiro di sollievo: il valore dell'integrazione può essere definito come il valore limite a cui tende una sommatoria di intervalli sempre più piccoli. Oggi un matematico spiegherebbe il concetto di infinitesimo come frutto di un fraintendimento: non si usano quantità più piccole di qualsiasi numero ma tuttavia non-nulle: si è semplicemente compiuta una operazione di passaggio al limite.

Ma in realtà il problema del bicchiere, a ben vedere, rimane: perché qualsiasi valore della sommatoria diverso dal valore limite è inesatto? L'infinito e i suoi paradossi erano irrimediabilmente penetrati nella matematica del Settecento con oggetti come le serie infinite e i limiti.

La definizione di limite di una successione di numeri è una delle più grandi scoperte della matematica, il pilastro di tutta l'analisi infinitesimale, e uno dei più bei concetti che l'ingegno umano abbia mai concepito:

Una successione di numeri reali è una funzione f : ℕ ➙ ℝ dall'insieme dei numeri naturali nell'insieme dei numeri reali. Di solito si scrive x₁ al posto di f(1), x₂ al posto di f(2), e così via.

Si dice che un numero x è il limite di una successione x₁, x₂, … se dato un qualsiasi numero reale ε > 0 esiste un numero naturale I tale che il valore assoluto di (x – x_n) è inferiore ad ε per ogni n > I

Una serie è la somma dei termini di una successione, finita o infinita, di numeri. Una serie infinita ha una somma calcolabile se e solo se la successione delle somme parziali dei suoi segmenti iniziali converge ad un limite.

Già Eulero, nel Settecento, aveva mostrato che si poteva calcolare, con una operazione di passaggio al limite, il valore di serie infinite convergenti.

Consideriamo il caso di un uomo che spende una somma S di 1000 fiorini per acquistare dei beni da un secondo uomo (il panettiere); supponiamo che il secondo uomo spenda una percentuale dell'80% di questa somma per acquistare beni presso un terzo uomo (il lattaio); il terzo uomo spende a sua volta l'80% di ciò che ha ricevuto presso un quarto uomo (il macellaio). Supponiamo di proseguire all'infinito questa serie:

1000 + 1000 · 0,8 + (1000 · 0,8) · 0,8 + ((1000 · 0,8) · 0,8) · 0,8 +…

e cioè:

1000 · (0,8)⁰ + 1000 · (0,8)¹ + 1000 · (0,8)² + 1000 · (0,8)³ + …

e cioè, chiamando la somma iniziale "S", la somma finale "∑" e la percentuale "c":

∑ = S · c⁰ + S · c¹ + S · c² + S · c³ + …

e cioè:

Come si può calcolare il valore di ∑, cioè il valore di una somma infinita?

A questo scopo, definiamo una nuova somma ∑₁:

∑₁ = ∑ · c

scriviamo, accanto a questa, una seconda, evidente, eguaglianza:

∑ – ∑₁ = S

mettiamo a sistema le due eguaglianze, considerando ∑ come incognita. Sostituiamo l'espressione per ∑₁ della prima, nella seconda, ottenendo:

∑ – (∑ ⋅ c) = S

e cioè:

∑ ⋅ (1 – c) = S

e cioè:

Notate che tutte le espressioni sono in realtà passaggi al limite.

Con simili metodi, Eulero mostrò che il numero e = 2,71828…, che da lui prende il nome, è il limite di una serie infinita di somme:

Generalizzando simili scoperte e definendo rigorosamente il concetto di limite, Augustin Louis Cauchy, agli inizi dell'Ottocento, mostrò che ci sono serie infinite che convergono ad un limite, e che tale limite è perfettamente calcolabile. I matematici successivi diedero le condizioni necessarie e sufficienti, valide per la maggior parte delle serie, per stabilire se esse siano convergenti o no.

Ma nonostante i matematici si stessero lentamente familiarizzando col concetto di infinito, esistevano ancora dei paradossi che li spaventavano. Alcuni però erano solo apparenti. Il compito di chiarire quali fossero apparenti e quali reali, di sondare l'effettiva estensione del dominio conquistabile, toccò a me.

il metodo assiomatico

back to index

[En 10] Oggetti matematici come le funzioni differenziabili e i numeri possono essere definiti come particolari tipi di insiemi. I teoremi della matematica, come ad esempio il teorema fondamentale del calcolo, possono essere espressi come proposizioni su insiemi, e provabili in base agli assiomi. Gli assiomi di ZFC forniscono una collezione sufficiente per lo sviluppo di tutta la matematica.

L'approccio non-assiomatico alla teoria degli insiemi è chiamato "naive set theory". Storicamente, questa è la forma in cui si originò la teoria degli insiemi. Ma ben presto i paradossi fecero orientare verso una trattazione assiomatica.

Le nozioni primitive sono "insieme" e "appartenenza".

Le conseguenze logiche degli assiomi sono chiamate teoremi.

[En 12] Un metateorema afferma che dato un sistema assiomatico, una qualsiasi conseguenza logica dei suoi assiomi ha una prova di lunghezza finita.

Una Teoria formale è creata a partire da un insieme contabile di simboli. Ecco i simboli della teoria degli insiemi:

∀x : per ogni insieme x

∃x : esiste un x tale che

∼ oppure ⌉ : non

& oppure ∧ : et

∨ : oppure (nel senso uno o l'altro o entrambi)

⇒ : implicazione (se… allora)

⇔ : biimplicazione (se e solo se)

∈ : appartiene a

= : è lo stesso oggetto

simboli per gli insiemi : normalmente lettere latine minuscole (a, b, c, …)

simboli per le classi : normalmente lettere latine maiuscole (A, B, C, …)

[En 22] In un sistema assiomatico esistono delle regole per stabilire quale successione di simboli sia dotata di significato ("formula ben formata" o "fbf") e quale no, come ad esempio: ")) ⇒ A"

Queste regole consistono in una definizione ricorsiva di fbf come segue:

"a ∈ B" e "a = b" sono fbf

Se φ e ψ sono fbf allora sono fbf anche "∀x φ", "∃x φ", "∼φ", "φ & ψ", "φ ∨ ψ", "φ ⇒ ψ", "φ ⇔ ψ"

Nessun'altra è una fbf all'infuori di queste (formula di chiusura)

[En 19] La maggior parte degli assiomi sono di forma esistenziale, e asseriscono l'esistenza di determinati insiemi: ∃B ∀x (x ∈ B ⇔ …) o, in forma più completa: ∀y₁ ∀y₂ … ∀y_k ∃B ∀x (x ∈ B ⇔ …)

gli assiomi della teoria degli insiemi

back to index

Una trattazione degli assiomi è in [Go 75], [En 17]

Cantor individuò dei paradossi, di alcuni dei quali accenneremo più avanti, ma non se ne curò particolarmente.

Ernst Zermelo, Abraham Fraenkel, Paul Bernays, Janos von Neumann, Alfred Tarski, Kurt Gödel, crearono contemporaneamente la teoria assiomatica degli insiemi e la logica matematica. L'idea originaria di Zermelo era di individuare un piccolo numero di assiomi da cui tutta la teoria degli insiemi potesse essere dedotta logicamente senza contraddizioni. Entro tale teoria si sarebbe potuta costruire con sicurezza la nozione di numero.

Elenco degli assiomi:

Assioma di estensionalità

Assioma dell'insieme vuoto

Assioma della coppia (pairing axiom)

Assioma di separazione ([En 18] Subset axiom; Aussonderungsaxiom)

Assioma dell'insieme potenza (power set axiom)

Assioma dell'unione

Assioma dell'infinito

Assioma di rimpiazzamento

Assioma di regolarità (fundierungsaxiom; assioma di fondazione)

Assioma di scelta

[Go 75 ss.] Ecco una breve definizione per ciascun assioma:

▸ Assioma di estensionalità: Due insiemi sono uguali se e solo se contengono gli stessi elementi. In simboli:

∀x ∀y (x = y ⇔ ∀z (z ∈ x ⇔ z ∈ y))

▸ Assioma dell'insieme vuoto: Esiste un insieme che non contiene alcun elemento. In simboli:

∃x ∀y (y ∉ x)

▸ Assioma delle coppie: Dati due qualsiasi insiemi, esiste un insieme i cui elementi sono precisamente questi insiemi. In simboli:

∀x ∀y ∃z ∀w (w ∈ z ⇔ (w = x ∨ w = y))

▸ Assioma di separazione: Dato un qualsiasi insieme x esiste un insieme che consiste di tutti gli elementi z di x per i quali vale la proprietà predicata dalla proposizione o formula logica φ(z). In simboli:

∀x ∃x ∀z (z ∈ y ⇔ (z ∈ x & φ(z)))

▸ Assioma dell'insieme potenza: Dato un qualsiasi insieme, esiste l'insieme che ha come elementi tutti i sottoinsiemi di x. In simboli:

∀x ∃y ∀z (x ∈ y ⇔ z ⊆ x)

▸ Assioma dell'unione: Dato un qualsiasi insieme x, esiste un insieme che è l'unione degli elementi di x. In simboli:

∀x ∃y ∀z (z ∈ y ⇔ ∃w (z ∈ w & w ∈ x))

▸ Assioma dell'infinito: Esiste un insieme induttivo. In simboli:

∃x (∅ ∈ x & ∀y (y ∈ x ➙ y ∪ {y} ∈ x))

▸ Assioma di rimpiazzamento: Se φ(s,t) è una funzione-classe, allora quando il suo dominio è ristretto ad x l'immagine risultante forma un insieme y. In simboli:

∀x ∃y ∀y' (y' ∈ y ⇔ ∃x' (x' ∈ x & φ(x', y')))

∀s ∃t (φ(s, t) & ∀t' (φ(s,t') ➙ t = t'))

▸ Assioma di fondazione: [Go 92, 95] Ogni insieme è ben-fondato, cioè contiene un elemento minimo nell'ordine dato dall'appartenenza ∈ (∈-minimal element) In simboli:

∀x ∃y (y ∈ x & x ∩ y = ∅)

Un minimal element y nella relazione ∈ è tale che non esiste un altro elemento dell'insieme x che sia con y in relazione di appartenenza. Per escludere questo è necessario appunto postulare che x e y non abbiano elementi in comune, altrimenti esisterebbero degli elementi di x inclusi in y

▸ Assioma di scelta: Si supponga che F è una famiglia di insiemi non-vuoti. Allora esiste una funzione f da F a ∪F (unione di F: insieme degli elementi degli elementi di F) tale che per ogni A che appartiene ad F, l'immagine f(A) appartiene ad A.

Ecco ora una trattazione approfondita di singoli assiomi:

assioma di rimpiazzamento

back to index

[Go 93] L'assioma di rimpiazzamento:

∀x ∃y ∀y' (y' ∈ y ⇔ ∃x' (x' ∈ x & ϕ(x',y')))

dove ϕ(s,t) è una formula tale che

∀s ∃t (ϕ(s,t) & ∀t' (ϕ(s,t') ➙ t' = t))

Se ϕ(s,t) è una class function,allora quando il suo dominio è ristretto ad x l'immagine forma un insieme.

[Go 94] Ora, restringiamo l'elemento s ad un insieme x come dominio:

{〈s,t〉 | s ∈ x & ϕ(s,t)}

L'assioma di rimpiazzamento ci dice che esiste un insieme y a cui appartengono le immagini, anzi ci dice che esiste un insieme y consistente esclusivamente di queste immagini. Quando ϕ(s,t) ha queste caratteristiche, l'insieme sopra indicato definisce una funzione in ZF.

L'assioma di rimpiazzamento garantisce l'esistenza di un insieme

{ℕ, P(ℕ), P(P(ℕ))…}

che è importante per la teoria degli infiniti di Cantor. L'assioma garantisce che è un insieme. Inoltre garantisce che possiamo definire funzioni su ℕ in modo ricorsivo.

assioma di separazione

back to index

Vedi intestazione "Il metodo di astrazione e i suoi paradossi"

assioma dell'unione

back to index

[En 24] Notare che non si tratta dell'affermazione che dati due insiemi ne esiste l'insieme unione, ma che dato un insieme, esiste il suo insieme unione, che non è altro che l'insieme risultante dalla "rottura dei sacchi", come si è espresso un autore (Lolli), cioè ottenuto prendendo gli elementi degli insiemi che compongono l'insieme.

assioma di fondazione

back to index

In ZFC, come conseguenza dell'assioma di fondazione, un insieme non può appartenere a se stesso, l'insieme di tutti gli insiemi non è un insieme, non esistono infinite descending ∈-chains, non si può avere x ∈ y e y ∈ x

l'assioma di scelta (ac)

back to index

[Go 112] Zermelo voleva provare il principio del buon ordinamento per tutti gli insiemi, e introdusse AC. I matematici non erano interessati ad un principio generale, ma solo al buon ordinamento di ℝ. Essi dubitavano che si potesse formulare un principio generale. La prova di Zermelo attraverso AC fu guardata con sospetto, soprattutto perché collegava la funzione di scelta, che non era molto controversa (si riteneva plausibile che potesse essere derivata dagli altri assiomi della teoria degli insiemi) con un principio controverso come WO. Ma la cosa importante fu che vennero individuate con precisione le prove che facevano uso in modo surrettizio di qualche forma di AC, e il lavoro di Zermelo mostrò che AC equivale in realtà a WO.

[Go 112] Per risolvere la questione se accettare o no AC i matematici speravano di poter mostarre che AC era provabile oppure dimostrare falso a partire dagli altri assiomi di ZF. Nel 1940 Gödel mostrò che AC era coerente con il resto degli assiomi di ZF, cosicché non era dimostrabile come falso in ZF. Nel 1963 Cohen provò che AC era indipendente da ZF, e quindi non poteva nemmeno essere provato a partire dagli assiomi di tale teoria. A questo punto, accettare o meno AC rimane una scelta del singolo matematico.

ac: formulazioni equivalenti

back to index

Vedi intestazione nella sezione sui numeri transfiniti: "Le varie forme dell'assioma di scelta. Prova che AC implica WO"

ac: ciò che può essere provato senza ac e ciò che può essere provato solo con ac

back to index

[Ho 53] Senza AC non si può dimostrare che ogni insieme infinito ha un sottoinsieme contabilmente infinito.

[En 48] Senza AC non si può dimostrare che ogni funzione possiede una inversa destra. Data una funzione f : A ➙ B, una funzione inversa destra di f è una funzione h tale che h ∘ f = I_A (funzione identità di A) e una funzione inversa sinistra è una funzione g tale che g ∘ f = I_B (identità di B). L'inversa f^–1, se fosse una funzione sarebbe precisamente l'inversa destra, ma non è detto che lo sia, perché f potrebbe non essere iniettiva. Nel caso non sia iniettiva, possono esistere elementi b di B che sono immagini di più elementi di A, e senza una struttura entro f^–1(b) non si ha modo di selezionare un solo elemento.

il metodo di astrazione e i suoi paradossi

back to index

L'obiettivo di Frege era di ridurre la matematica all'insiemistica e l'insiemistica alla logica. Questo indirizzo di pensiero viene chiamato logicismo. Per ridurre la teoria degli insiemi alla logica, Frege stabilì una corrispondenza tra ciascuna delle proprietà predicabili di un qualsiasi oggetto e un insieme. Se la proprietà P è predicabile degli oggetti a, b, c, d e di nessun altro, allora essa corrisponde all'insieme {a,b,c,d}. Viceversa, possiamo descrivere un insieme fornendo la proprietà che hanno i suoi elementi e nessun altro. Questo metodo di descrivere insiemi è molto potente, e viene detto principio di astrazione:

{x | x è rosso}

è l'insieme degli oggetti rossi

{x | x è umano e x è nato in Inghilterra}

definisce l'insieme di tutti gli inglesi (secondo una possibile definizione di questo popolo). E così via.

E' proprio questo metodo che è stato usato da Frege per costruire i suoi numeri naturali: uno è l'insieme i cui elementi hanno la proprietà di essere insiemi e di avere un solo elemento:

{x | x è un insieme e x possiede un solo elemento}

due è l'insieme i cui elementi hanno la proprietà di essere insiemi e di possedere due elementi:

{x | x è un insieme e x possiede due elementi}

e così via.

Il "paradosso" degli insiemi che appartengono a se stessi. Ma proprio questo modo di definire insiemi nasconde paradossi. Prendiamo ad esempio l'insieme V di tutti gli insiemi. Allora V deve appartenere a se stesso: V ∈ V. Questo contraddice la nostra idea intuitiva di un insieme come collezione di oggetti materiali che, in quanto tale, non può appartenere a se stessa.

Il paradosso di Russell. Ma il paradosso più grave, noto come paradosso di Russell, (fu indipendentemente scoperto da Zermelo) è il seguente. Consideriamo l'insieme S di tutti gli insiemi che non appartengono a se stessi. Chiediamoci: S appartiene a se stesso? Se diciamo che S appartiene a se stesso, allora S non può appartenere a se stesso, perché gli appartengono solo gli insiemi che non appartengono a se stessi. Se diciamo che S non appartiene a se stesso, allora S appartiene a se stesso, perché in tale insieme sono compresi proprio gli insiemi che non appartengono a se stessi. Quale che sia l'affermazione su S, essa genera una contraddizione con altre affermazioni che abbiamo fatto su S.

Pertanto, non può essere utilizzato, per fondare la teoria degli insiemi, un assioma del tipo:

∃y ∀x (x ∈ y ⇔ φ(x))

dove φ(x) è una qualsiasi proposizione che enuncia che x ha una o più proprietà. E' detto assioma di astrazione. E' il quinto assioma del sistema logico esposto da Gottlob Frege nel suo Grundgesetze der Arithmetik del 1893. Senza di esso l'intero sistema – e in particolare la nozione di numero – crolla come un castello di carte. Bertrand Russell comunicò a Frege questo paradosso in una sua famosa lettera del 1902: Frege cadde in una crisi depressiva e non pubblicò più nulla per molti anni.

Il paradosso di Berry. [En 5] Consideriamo l'insieme:

{x | x è un intero positivo definibile in una sola riga di testo}

Poiché esiste solo un numero finito di tipi di caratteri e un numero finito di posti in una riga l'insieme di cui sopra è un insieme finito di numeri interi. Ora consideriamo la seguente definizione:

"il più piccolo intero positivo non definibile con una sola riga di testo"

Tale intero è definito in una riga di testo, quindi dovrebbe essere compreso nell'insieme, ma, per sua definizione, non vi è compreso. Questo mostra che

[En 22] L'approccio assiomatico rende il paradosso di Berry impossibile, perché la formula:

∃B ∀x (x ∈ B ⇔ x ∈ ω & x è un intero definibile in una riga di testo)

non è una fbf in ZF, in quanto "definibile in una riga di testo" non è una espressione rappresentabile con i simboli a nostra disposizione.

come viene evitato il paradosso di russell in zfc

back to index

Il paradosso di Russell, come è noto, deriva dall'assioma di astrazione, il quinto assioma del sistema logico esposto dal matematico Gottlob Frege nel suo Grundgesetze der Arithmetik del 1893:

∃y ∀x (x ∈ y ⇔ φ(x))

dove φ(x) è una proprietà espressa da una formula ben formata (fbf) del linguaggio del secondo ordine.

Scegliendo come proprietà:

φ(x) = x ∉ x

avremo:

∃y ∀x (x ∈ y ⇔ x ∉ x)

Ponendo x = y per l'arbitrarietà di x otteniamo:

∃y (y ∈ y ⇔ y ∉ y)

che è il paradosso che Bertrand Russell comunicò con una celebre lettera del 1901 a Gottlob Frege annunciandogli in tal modo il fatale difetto del suo intero sistema logico.

Come l'assioma di separazione elimina il paradosso di Russell

Per evitare questa difficoltà, un brillante allievo di David Hilbert, Ernst Zermelo, che Hilbert aveva indirizzato allo studio delle opere di Cantor, Frege e Russell, aveva introdotto nella sua assiomatizzazione della teoria degli insiemi, il cosiddetto "assioma di separazione" (Aussonderungsaxiom nell'originale tedesco), che può essere formulato in questo modo:

∀z ∃y ∀x (x ∈ y ⇔ x ∈ z ∧ φ(x))

dove φ(x) è definito come sopra (notare che in tale assioma z deve essere un insieme)

Secondo questo principio è ammessa la comprensione delle proprietà solo nell'ambito di insiemi già precostituiti, nel senso che la loro esistenza o è stata postulata o può essere dimostrata nel sistema.

Con l'assioma di separazione non è più possibile derivare una contraddizione introducendovi la proprietà:

φ(x) = x ∉ x

Avremo infatti:

∀z ∃y ∀x (x ∈ y ⇔ x ∈ z ∧ x ∉ x)

Per l'arbitrarietà di x poniamo x = y e scriviamo:

∀z ∃y (y ∈ y ⇔ y ∈ z ∧ y ∉ y)

la biimplicazione:

y ∈ y ⇔ y ∈ z ∧ y ∉ y

non può essere vera in virtù della verità di entrambi i membri. Pertanto, per essere vera (e la formula deve essere vera, perché è un assioma), entrambi i membri devono essere falsi (vedi la tavola di verità della biimplicazione):

∼( y ∈ y ⇔ y ∈ z ∧ y ∉ y)

ma se il primo membro è falso allora deve essere:

∼( y ∈ z ∧ y ∉ y)

ma la falsità del primo membro ci dice che y ∉ y è vero; l'unica possibilità di falsificazione della formula è quindi:

∀z ∃y ∼(y ∈ z)

e cioè:

∀z ∃y (y ∉ z)

che non è contraddittoria, e ci dice semplicemente che non esiste un insieme "universale" che comprende tutti gli insiemi, perché per qualsiasi insieme z esisterà sempre un elemento y che non gli appartiene.

L'assioma di separazione implica l'inesistenza di un insieme universale

Possiamo sviluppare ulteriormente la formula di cui sopra:

∀z ∃y (y ∈ y ⇔ y ∈ z ∧ y ∉ y)

per trarne un'altra proposizione non-contraddittoria: quella sulla inesistenza di un insieme che contiene tutti gli insiemi. Esporremo tre diverse dimostrazioni, dovute, rispettivamente a Patrick Suppes (Axiomatic Set Theory), a Paul Halmos (Naive Set Theory) e ad Herbert Enderton (Elements of Set Theory)

dimostrazione di suppes:

Sostituiamo nella formula y a z ottenendo:

∃y (y ∈ y ⇔ y ∈ y ∧ y ∉ y)

questa biimplicazione è vera solo alla condizione che i due membri siano falsi, e cioè a condizione che sia:

∃y (y ∉ y)

che è l'asserzione che esiste almeno un insieme che non include se stesso.

dimostrazione di halmos:

La dimostrazione di Halmos parte dalla formula più generale ottenuta sostituendo nell'assioma y ad x:

∀z ∃y (y ∈ y ⇔ y ∈ z ∧ y ∉ y)

Chiediamoci se y appartenga a z: è possibile provare che in realtà y ∉ z. Osserviamo a questo scopo la biimplicazione di cui sopra:

y ∈ y ⇔ y ∈ z ∧ y ∉ y

Si può avere y ∉ z nel membro di destra con il membro di sinistra vero o con il membro di sinistra falso. Nel primo caso deve essere vero y ∉ y, il che conduce ad una contraddizione. Nel secondo caso deve essere y ∉ z, perché solo questa condizione può determinare la falsità del secondo membro. Abbiamo così dimostrato, data l'arbitrarietà di z, che esiste comunque un y che non appartiene a z.

Questa proposizione, a prescindere dal fatto che è assiomaticamente derivata, può essere provata anche con un semplice esempio. Consideriamo l'insieme

A = {{1},{2}}

E' chiaro che A non appartiene a se stesso:

A ∉ A

Viene in tal modo confermata l'esistenza di un y tale che y ∉ y.

dimostrazione di enderton:

[En 22] Dato un insieme A, costruiamo, con l'assioma di separazione, un insieme B che non appartiene ad A:

B = {x ∈ A | x ∉ x}

Si ha:

B ∈ B ⇔ B ∈ A & B ∉ B

Se B ∈ A la formula si ridurrebbe a:

B ∈ B ⇔ B ∉ B

che è contraddittoria: se ne conclude che B ∉ A

[En 22] Se combiniamo l'assioma di separazione con l'assioma di fondazione, che implica che nessun set appartiene a se stesso, ne concludiamo che questo insieme B non è altro che l'insieme A.

L'insieme di tutti gli insiemi è in effetti un insieme ingombrante e non necessario. Esistono tuttavia sistemi in cui ne è ammessa l'esistenza, come ad esempio NBG ([Suppes 29]). Anche il meno noto sistema di Quine ammette l'insieme universale.

Dalla inesistenza di un insieme di tutti gli insiemi, si può derivare facilmente l'inesistenza del "complemento assoluto", cioè l'insieme che contiene tutti gli elementi che non appartengono ad un dato insieme S.

L'assioma di separazione è necessario per stabilire l'esistenza dell'insieme intersezione

[En 21] L'assioma di separazione, tra l'altro, è necessario per stabilire l'esistenza di insiemi importanti, come l'insieme intersezione, l'insieme dei naturali pari

Una diversa dimostrazione dell'inesistenza del paradosso di Russell in ZFC (Takeuti-Zaring)

G. Takeuti e W.M. Zaring espongono una diversa dimostrazione di come gli assiomi di ZFC impediscano il paradosso di Russell, che, per completezza, esporremo qui di seguito.

Accanto ai termini primitivi, che sono lettere minuscole, introduciamo come altro termine la classe denotata con

{x | φ(x)}

mediante la definizione:

a ∈ {x | φ(x)} ≡ φ(a)

Il simbolo {x | φ(x)} non denota altro che "tutti gli x che hanno la proprietà φ".

Utilizzeremo ora, accanto alle lettere minuscole x, y, ecc., anche lettere maiuscole A, B, ecc. per indicare termini del primo o del secondo tipo.

Consideriamo la definizione:

A = B ≡ ∀x (x ∈ A ⇔ x ∈ B)

Utilizziamo lettere maiuscole A, B, ecc. per indicare un termine generico, del primo o del secondo tipo, e due predicati per tale termine, quello di essere una classe propria e quello di essere un insieme:

M(A) ≡ ∃x (x = A)

che si legge: "gli insiemi sono tutti e soli quelli denotati da variabili individuali o quelli denotati da termini che si può mostrare equivalenti (applicando la decostruzione delle definizioni) a oggetti denotati da variabili individuali"

Pr(A) ≡ ∼M(A)

che si legge: "i termini che non denotano insiemi sono classi proprie"

Si ricava facilmente il seguente teorema:

∀x M(x)

Dato l'insieme Ru definito come:

Ru = {x | x ∉ x}

si ha il teorema:

Pr(Ru)

perché diversamente si avrebbe:

∃y (y = Ru)

∃y ∀x (x ∈ y ⇔ x ∉ x)

∃y (y ∈ y ⇔ y ∉ y)

e cioè:

M(Ru) ➙ (Ru ∈ Ru ⇔ Ru ∉ Ru)

che è una contraddizione.

Quindi è:

∼M(Ru)

e cioè

∼∃x (x = Ru)

Una volta dimostrato che non esiste l'insieme degli insiemi che non appartengono a se stessi il paradosso di Russell è risolto.

le definizioni mediante astrazione in zfc

back to index

[En 27] Nella naive set theory si incontrano in ogni momento definizioni per astrazione:

A ∪ B = {x | x ∈ A ∨ x ∈ B}

A ∩ B = {x | x ∈ A & x ∈ B}

A – B = { x ∈ A | x ∉ B}

Questo pone due ordini di problemi: a) garantire mediante definizione la traducibilità in una fbf di ZFC; b) provare che l'oggetto esiste ed è un insieme

In alcuni casi (ad esempio nel sistema NBG) la definizione per astrazione può legittimamente dare luogo a classi.

le classi

elenco di collezioni che non sono insiemi ma classi

back to index

Il complemento assoluto. [En 27] Non possiamo formare il complemento assoluto B di un insieme A come insieme perché l'unione di A e B darebbe un insieme che comprende tutti gli insiemi, perché dagli assiomi ZFC si ricava che l'unione di due insiemi è un insieme.

La classe degli insiemi che non appartengono a se stessi. (vedi la trattazione del paradosso di Russell)

L'insieme universale. L'assioma di separazione implica che non esista (vedi trattazione paradosso di Russell)

annotazioni varie di teoria degli insiemi

back to index

La definizione di coppia ordinata. Il matematico Kazimierz Kuratowski, nel 1921, ha trovato la definizione di coppia ordinata in uso ancora oggi:

<x,y> ≡ {{x}, {x,y}}

Le relazioni. Le relazioni non sono necessariamente binarie, ma normalmente sono n-arie

Terminologia delle funzioni estendibile alle relazioni. [En 40] Dominio di una relazione. Range di una relazione. Relazione single rooted corrispondente al concetto di iniettività (relazioni binarie).

l'intersezione di un insieme vuoto

back to index

[En 25] Se definiamo l'intersezione di un insieme secondo la formula:

x ∈ ∩A ⇔ x appartiene a ogni elemento di A

allora è vero in senso vuoto ("vacuously true") che x appartiene a ogni elemento di ∅, e quindi parrebbe che ∩∅ sia la classe V di tutti gli insiemi. Ma come sappiamo, questo non è un insieme, ma una classe, tra l'altro perché, per l'assioma di separazione, dato un insieme, esiste sempre un insieme che non gli appartiene. Ma noi vogliamo definire ∩∅ come un insieme. Una opzione è di lasciare ∩∅ indefinito, dato che non esiste un modo soddisfacente di definirlo. Questa scelta funziona bene, ma ad alcuni logici non piace. L'altra opzione è trovare un "capro espiatorio", ad es. ∅ stesso, e definire ∩∅ = ∅. In qualsiasi modo ci si orienti, quando si costruisce l'intersezione ∩A di un insieme, occorre stare attenti alla possibilità che A = ∅. Enderton suggerisce che, dal momento che non fa nessuna differenza quale delle due opzioni abbracciamo, possiamo non curarci di fare una scelta.

cumulative hierarchy of sets (la gerarchia cumulativa degli insiemi)

back to index

[Go 96] La gerarchia cumulativa degli insiemi è un processo iterativo che alterna l'operazione di passaggio all'insieme potenza a quella di unione generalizzata, a partire dal minimo numero di oggetti necessario. Ad ogni passo viene generata una collezione di nuovi insiemi V_i, con gli indici i che sono numeri ordinali, indicizzata in base al numero dei passi che sono stati necessari a crearla. La chiameremo CHS.

Una CHS può essere generata sia in un sistema assiomatico che ammette urelemente, sia in un sistema assiomatico che non li ammette, come ZF. Una delle costruzioni possibili nel caso di ZF è la costruzione a partire dal solo insieme vuoto.

[q] Gli elementi di CHS sono ordinati per inclusione. Questo non contraddice il teorema (derivato dal Fundierungsaxiom) secondo cui non esistono catene di appartenenza discendenti infinite (infinite descending ∈-chains): infatti, nel caso di CHS si tratta di catene di appartenenza ascendenti infinite (infinite ascending ∈-chains), e poi si tratta di sequenze entro insiemi, mentre V non è un insieme.

Costruzione di CHS in un sistema con urelemente (Enderton)

[En 7] V₀ è l'insieme degli atomi

V₁ = V₀ ∪ P(V₀)

V₂ = V₁ ∪ P(V₁)

Per V_ω prendiamo l'unione infinita: V_ω = V₀ ∪ V₁ ∪ V₂, …

V_ω+1 = V_ω ∪ P(V_ω)

Costruzione di CHS a partire dall'insieme vuoto (Goldrei)

[Go 225] I passi per la creazione della CHS a partire dal solo insieme vuoto sono i seguenti:

V₀ = ∅

V_γ₊ = P(V_γ)

V_λ = ∪{V_γ | γ ∈ λ} per un ordinale limite λ

[Go 97] dove i V_i sono indicizzati dagli ordinali.

[Go 97] Abbiamo cioè, costruendo i primi livelli a titolo di esempio:

V₀ = ∅

V_n+ = P(V_n), per n ∈ ℕ

V_ω = ∪{v_n | n ∈ ℕ}

Ripetiamo il processo di successione mediante insieme potenza su V_ω ottenendo una ulteriore serie:

V_ω, P(V_ω), P(P(V_ω)), …

Poi ripetiamo il processo di unione generalizzata, comprendendovi tutti i precedenti V_i:

∪{V₀, V₁, V₂, …, V_ω, , P(V_ω), P(P(V_ω)), …}

La costruzione va avanti alternando la costruzione di successori mediante l'insieme potenza e l'unione generalizzata.

[En 9] mostra che si può anche scrivere V_γ+ = V_γ ∪ P(V_γ), perché tanto, con l'insieme vuoto come V₀, V_γ ∪ P(V_γ) = P(V_γ)

[En 9] Proviamo a vedere di cosa consistono i primi livelli:

V₀ = ∅

V₁ = P(∅) = {∅}

V₂ = P(P(∅)) = {∅, {∅}}

V₃ = P(P(P(∅))) = {∅, {∅}, {∅, {∅}}}

V₄ = P(P(P(P(∅)))) = { ∅, {∅}, {∅, {∅}}, {∅, {∅}, {∅, {∅}}}, {∅, {∅, {∅}}}, {{∅}, {∅, {∅}}} }

………………………………………..

Vediamo che si tratta della successione di ordinali:

V₀ = 0

V₁ = 1

V₂ = 2

V₃ = 3

Gli insiemi che compaiono in ogni livello non sono tuttavia solo ordinali; ad es V₄ comprende anche gli insiemi:

{∅, {∅, {∅}}}

{{∅}, {∅, {∅}}}

che non sono ordinali perché non sono transitivi, anche se sono ordinati dalla relazione di appartenenza. Inoltre, se è dimostrabilmente vero che tutti gli insiemi devono comparire in CHS, allora devono esserci insiemi come ω + 1, che non è un ordinale (anche se è order isomorphic ad un ordinale), ottenuti indicizzando ω ed 1 rispettivamente con 0 ed 1.

Dimostrazione che CHS contiene ogni insieme di ZF

[Go 97 riga 12, 226] Si può dimostrare che ogni insieme di ZF apparirà in qualche livello di CHS, quindi CHS non è altro che l'universo V di tutti gli insiemi.

[En 9] Questa affermazione è anche vera in un sistema con urelemente.

Il rango degli insiemi in CHS

[Go 229] Ogni insieme x nella CHS ha un rango ρ(x), che è dato dal least ordinal α tale che x ∈ V_α+

[En 9] Il rango di x può anche essere definito come il minimo α tale che x ⊆ V_α.

i numeri transfiniti

rassegna delle operazioni aritmetiche tra insiemi

back to index

▸ Addizione ordinale

[Go 232] Definiamo l'addizione ordinale, per un ordinale dato α e tutti gli ordinali β, come segue:

α + 0 = α

α + γ⁺ = (α + γ)⁺

α + λ = ∪{α + γ | γ ∈ λ} per un ordinale limite λ

[Go 241] L'addizione ordinale è associativa

▸ Moltiplicazione ordinale

[Go 232] Definiamo la moltiplicazione ordinale, per un dato ordinale α e tutti gli ordinali β, come segue:

α ⋅ 0 = 0

α ⋅ γ⁺ = (α ⋅ γ) + α

α ⋅ λ = ∪{α ⋅ γ | γ ∈ λ} per un ordinale limite λ

[Go 242] La moltiplicazione ordinale è associativa

▸ Esponenziazione ordinale

[Go 232] L'esponenziazione ordinale è definita in modo da coincidere con la definizione equivalente per i numeri naturali, cioè gli ordinali finiti, e utilizza la moltiplicazione in modo simile, stavolta di ordinali. Per un dato ordinale α e tutti gli ordinali β:

α⁰ = 1

α^γ+ = (α^γ) ⋅ α

α^λ = ∪{α^γ | γ ∈ λ} per un ordinale limite λ

[Go 239] Attenzione: la moltiplicazione ordinale non è commutativa: 2 ⋅ ω = ω ≠ ω ⋅ 2

▸ Somma cardinale

[Go 270] card(X) + card(Y) = card((X x {0}) ∪ (Y x {1}))

[En 139] card(X) + card(Y) = card(K + L) dove K,L sono due qualsiasi insiemi disgiunti di cardinalità card(X) e card(Y) rispettivamente

▸ Moltiplicazione cardinale

[Go 270] card(X) ⋅ card(Y) = card(X x Y)

[En 139] card(X) ⋅ card(Y) = card(K x L) dove K,L sono due qualsiasi insiemi di cardinalità card(X) e card(Y) rispettivamente

▸ Esponenziazione cardinale

[Go 270] card(X)^card(Y) = card(X^Y)

[En 139] card(X)^card(Y) = card(^KL) dove K,L sono due qualsiasi insiemi di cardinalità card(X) e card(Y) rispettivamente

[Lo 165] Se h e k sono cardinali, h^k per definizione è la cardinalità di ^kh, cioè dell'insieme di tutte le funzioni da (un insieme di cardinalità) k in (un insieme di cardinalità) h. Nel caso finito, l'operazione coincide col solito elevamento a potenza.

la definizione rigorosa dei vari sistemi di numeri, dai reali (sezioni di dedekind) ai naturali (peano e cantor)

back to index

Gli ordinali finiti, incidentalmente, vennero a colmare una lacuna nel processo di consolidamento delle fondamenta della matematica.

Le nuove scoperte nel campo dell'analisi, ad opera di Cauchy, Bolzano, Weierstrass e dei loro allievi crearono, intorno alla metà dell'Ottocento, la necessità di porre la mole di conoscenze sino ad allora acquisite su fondamenta più rigorose, e si sentì il bisogno di definire in modo preciso i numeri reali, i numeri razionali e i numeri interi, la cui nozione era rimasta a dir poco vaga.

Nel 1872 la prima parte di questa impresa era stata portata a termine: un articolo di Richard Dedekind aveva finalmente proposto una soddisfacente definizione dei numeri reali in termini di sezioni di numeri razionali⁽⁵⁾. I razionali erano già stati definiti come classi di equivalenza di coppie di interi⁽⁶⁾, e gli interi come classi di equivalenza di coppie di numeri naturali⁽⁷⁾. Il lavoro di Cantor e quello di Giuseppe Peano fornirono le fondamenta mancanti: la definizione rigorosa di numero naturale.

Nel 1898 il matematico e logico italiano Giuseppe Peano definì quelli che sono noti come assiomi di Peano:

X è un insieme con un elemento speciale 0 e una funzione S da X ad X chiamata "funzione successore", tale che valgono le seguenti proprietà:

(i) la funzione S è iniettiva

(ii) per tutti gli x appartenenti ad X, l'elemento 0 non immagine di tali elementi

(iii) se un qualsiasi sottoinsieme A di X contiene l'elemento 0 e contiene S(x), cioè il successore di x ogniqualvolta x appartenga ad A, allora A coincide con X

Ogni insieme ordinato e dotato di un'operazione di successione che soddisfa questi assiomi è chiamato un sistema di Peano. I numeri naturali sono un sistema di Peano (in effetti gli assiomi furono dati proprio per definirne le proprietà fondamentali).

La straordinaria importanza degli assiomi di Peano è stata quella di aver svincolato lo studio dei naturali dal modello numerico, aprendo la strada ad altri modelli, come quello insiemistico, che si sarebbero rivelati estremamente efficaci per studiarne le proprietà.

In particolare, l'insieme degli ordinali finiti, definito come sopra, con l'ordine dato dall'inclusione e la definizione di ordinale successore, soddisfa gli assiomi di Peano. Da allora l'insieme ω degli ordinali finiti fornì ai matematici un modello per lo studio delle proprietà dei numeri naturali e nei testi ω viene alternativamente definito insieme dei numeri naturali o costruzione insiemistica dei numeri naturali o numeri naturali entro la teoria degli insiemi o numeri naturali entro ZFC.

gli ordinali

le relazioni d'ordine

back to index

[Go 188] Cantor sviluppò il sistema degli ordinali come mezzo per estendere oltre il finito l'idea di numerare gli stadi di un processo – "prima fa' questo, poi quello, poi quell'altro…". Se rappresentiamo questi stadi con gli elementi di un insieme ordinato X, allora richiediamo implicitamente che per ogni dato stadio x ci sia uno stadio "successivo" (a meno che x non sia lo stadio "finale", cioè l'elemento massimo di X). Così, se x non è il massimo elemento di X, nel qual caso l'insieme degli elementi che seguono x nell'ordine è vuoto, noi richiederemo che questo insieme contenga un elemento minimo x⁺. Andando un tantino al di là di questo requisito minimo, richiederemo che in un insieme ben-ordinato ogni sottoinsieme non vuoto abbia un elemento minimo.

Cantor si volse a studiare le relazioni d'ordine.

Il primo infinito, l'insieme dei numeri naturali non ha solo una dimensione, che Cantor era riuscito a misurare e comparare, ma anche un ordine, per cui, dati due numeri, si può dire che uno precede e l'altro segue. Cantor indagò le caratteristiche peculiari di questo ordine:

▸ n R n : l'ordine dei naturali è irriflessivo: un numero n non è in rapporto R con se stesso

▸ ((m R n) & (n R p)) ➙ m R p : l'ordine è transitivo: se un numero è in rapporto con un altro e questo a sua volta con un terzo, anche il primo e il terzo sono in rapporto.

▸ ∀n ∀m ((n R m) ∨ (m R n) ∨ (m = r)) : l'ordine soddisfa la legge di tricotomia o linearità: dati due numeri, essi sono uguali o in relazione tra loro

▸ ∀S ≠ ∅ ⊆ ℕ (∃ n ∈ S (∀m ∈ S (n R m))) : l'ordine è un buon ordine: ogni sottoinsieme non vuoto di ℕ, insieme dei naturali, compreso ℕ stesso, possiede un elemento minimo, minore di tutti gli altri elementi dell'insieme. Invece, l'insieme ℤ dei numeri interi non è ben ordinato, perché ℤ, considerato come sottoinsieme di se stesso, non ha un elemento minimo: infatti, qualsiasi numero n intero si prenda esiste sempre un intero m che lo precede nell'ordine, talché n non può essere elemento minimo.

Le prime tre caratteristiche individuano quella che si chiama una relazione lineare di ordine stretto: irriflessiva, transitiva, lineare.

Una relazione riflessiva, transitiva e lineare è invece detta relazione lineare di ordine debole.

Una relazione di ordine debole o di ordine stretto può anche essere non lineare.

La relazione "<", "maggiore di" tra i numeri naturali è una relazione di ordine stretto lineare, mentre la relazione "≤", "maggiore o uguale a" tra i numeri naturali è una relazione di ordine debole lineare.

A ciascun ordine stretto lineare S corrisponde uno e un solo ordine debole lineare R ottenuto aggiungendo ad S l'insieme delle coppie identiche: (x,x), (y,y), … ecc.

A ciascun ordine debole lineare R corrisponde viceversa uno e un solo ordine stretto lineare ottenuto da R sottraendo l'insieme delle coppie identiche. Così, si può parlare senza ambiguità di ordine lineare, stretto o debole indifferentemente.

Agli elementi di un qualsiasi insieme finito si possono dare moltissimi buoni ordini che a prima vista sembrano diversi: ad esempio, nell'insieme {rosso, verde, giallo, blu, bianco, nero} i colori possono essere ordinati in 6! (fattoriale di 6) modi (successioni) diversi.

Ma in realtà si tratta di ordini identici. Cantor precisò il concetto di ordine identico definendo, per due insiemi X e Y ben ordinati da un ordine lineare una corrispondenza bijettiva f che mantiene l'ordine:

x₁ R_X x₂ ⇔ f(x₁) R_Y f(x₂)

dove R_X è la relazione d'ordine nell'insieme X e R_Y è la (diversa) relazione d'ordine nell'insieme Y.

Se due insiemi sono collegati da un simile isomorfismo d'ordine essi hanno ordini identici. Cantor chiamò tipo d'ordine la classe di tutti gli insiemi legati da un isomorfismo d'ordine.

E' abbastanza stupefacente scoprire che tutti gli insiemi finiti hanno in realtà un solo tipo di buon ordine lineare.

In particolare, nel caso di un insieme finito di numeri, qualsiasi possibile ordine è isomorfo a quello della successione aritmetica che ogni studente conosce: non ne esistono in realtà altri.

nel caso di un insieme infinito, ad una stessa cardinalità corrispondono più ordini possibili

back to index

Era dunque vero che ad una data cardinalità è associato un unico ordine? E se no, come si può contrassegnare ciascun ordine, visto che la matematica dei tempi di Cantor disponeva solo dei numeri cardinali e due ordini diversi avevano lo stesso cardinale?

La risposta alla prima domanda fu ottenuta subito: appare chiaro che esistono insiemi infiniti dotati della stessa cardinalità ma di ordini diversi. Prendiamo, ad esempio, l'insieme ω dei numeri naturali, togliamogli il numero 1 e mettiamolo alla fine, dopo la successione 2, 3, 4, 5, … Abbiamo creato un nuovo ordine, diverso da quello della successione 1, 2, 3, 4, 5, …

Quest'ordine viene denominato ω + 1. Da cosa si vede che si tratta di un ordine diverso? Dal fatto che ω + 1 possiede un punto limite, l'ultimo della serie, mentre ω non ne possiede. Un punto limite c di un insieme ordinato da un ordine stretto, non necessariamente lineare, è tale che esiste un punto a < c e per ogni a del genere esiste un d tale che a < d < c.

In modo simile si possono produrre ω + 2, ω + 3, … che sono ordini diversi l'uno dall'altro. Ma tutti questi insiemi sono equipotenti.

Per mostrare che ω e ω + 1 hanno la stessa cardinalità si può mettere ω in corrispondenza biunivoca con ω + 1 utilizzando la funzione identità :

f(n) = n

Questa stessa funzione collega ω a ciascuno degli altri ordini ω + 2, ω + 3, ω + 4, … mostrandone l'equipotenza.

la creazione dei numeri ordinali

back to index

Riepilogando: per ogni cardinalità infinita esistono infiniti ordini, e per ogni ordine esistono infiniti insiemi isomorfi. Occorreva trovare il modo di creare un modello più semplice possibile di insieme per ciascuna cardinalità e ciascuno degli ordini che potevano essere dati ad insiemi di quella cardinalità. Questo modello sarebbe stato, per i vari tipi di ordine, come il numero cardinale per i vari tipi di dimensione. Si tratta dei numeri ordinali.

La definizione di numero ordinale è ricorsiva.

Il primo ordinale è l'insieme vuoto: ∅

Il secondo ordinale è definito come l'unione del primo ordinale con l'insieme che lo contiene come solo elemento, cioè come ∅ ∪ {∅}, che dà l'insieme {∅}.

Il terzo ordinale è definito come l'unione del secondo ordinale con l'insieme che lo contiene come solo elemento: {∅} ∪ {{∅}}, e cioè {∅, {∅}}.

In modo simile sono definiti il quarto, il quinto, il sesto…, tutti gli ordinali successivi.

Ecco i primi ordinali:

∅ : lo zero

{∅} : l'uno

{∅, {∅}} : il due

{∅, {∅}, {∅, {∅}}} : il tre

La serie prosegue senza fermarsi:

{∅, {∅}, {∅, {∅}}, {∅, {∅}, {∅, {∅}}}} : il quattro

{∅, {∅}, {∅, {∅}}, {∅, {∅}, {∅, {∅}}},{∅, {∅}, {∅, {∅}}, {∅, {∅}, {∅, {∅}}}}} : il cinque

il sei

il sette

l'otto…

Questi ordinali, a parte lo zero, sono detti ordinali successori. Il procedimento per creare un ordinale successore è quello indicato più sopra. Formano l'insieme degli ordinali finiti, denominato col simbolo ω.

I numeri ordinali servono per classificare gli insiemi in cui sia stata definita una relazione di buon ordine: irriflessiva, transitiva, lineare e in cui ogni sottoinsieme possiede un elemento minimo. Per ogni insieme ben ordinato c'è un ordinale che gli è isomorfo (isomorfismo d'ordine). Ciascun segmento iniziale di un insieme ben ordinato è isomorfo (isomorfismo d'ordine) ad un ordinale.

le proprietà degli ordinali. gli insiemi transitivi. gli insiemi induttivi. definizione generale di numero ordinale.

back to index

Gli ordinali presentano varie simmetrie e proprietà. Ogni ordinale incorpora quelli successivi. Un ordinale contiene solo ordinali. All'interno di ciascun ordinale gli elementi sono ordinabili per inclusione e quest'ordine ha le caratteristiche di un buon ordine. Ogni ordinale è un insieme transitivo: i suoi elementi sono anche suoi sottoinsiemi. Tutti gli ordinali infiniti sono insiemi induttivi: un insieme A è induttivo se, oltre a possedere l'insieme vuoto, dato un qualsiasi elemento di A, appartiene ad A anche il suo successore. Omega ha l'ulteriore proprietà di essere il più piccolo degli insiemi induttivi. L'esistenza degli ordinali come insiemi induttivi necessita di un assioma, chiamato assioma dell'infinito, che stabilisca l'esistenza di almeno un insieme del genere:

∃x (∅ ∈ x & ∀y (y ∈ x ➙ y ∪ {y} ∈ x))

[Go 204] Una definizione semplice ed estremamente elegante di numero ordinale, che comprende sia gli ordinali finiti che gli ordinali infiniti è la seguente: un numero ordinale è un insieme transitivo ben-ordinato dalla relazione di appartenenza.

Un insieme transitivo è un insieme A ciascun elemento del quale è anche un insieme contenuto in esso:

a ∈ A ➙ a ⊆ A

Ecco alcune definizioni equivalenti di insieme transitivo:

x ∈ a ∈ A ➙ x ∈ A : un elemento di un elemento di A è un elemento di A

∪A ⊆ A : l'unione degli elementi contenuti in elementi di A è inclusa in A

A ⊆ P(A) : A è inclusa nel suo insieme potenza

Per vedere che ciascun ordinale successivo include gli ordinali precedenti come sottoinsiemi ma anche come elementi è sufficiente confrontare due qualsiasi ordinali successivi:

{∅, {∅}}

{∅, {∅}, {∅, {∅}}}

Si osserva immediatamente che il primo è incluso nel secondo.

E' facile vedere a questo punto che un insieme transitivo completamente ordinato dalla relazione di appartenenza deve possedere gli elementi di un ordinale e solo quegli elementi. Tutti gli insiemi hanno come sottoinsieme ∅. Quindi un insieme transitivo deve possedere ∅ come elemento. Poiché un insieme transitivo deve essere ordinato per inclusione, questo vuol dire che l'elemento successivo, nel caso l'ordinale abbia due elementi, deve contenere ∅. L'insieme transitivo non potrebbe avere come secondo elemento, oltre ∅, un insieme α diverso da ∅, perché non sarebbero ordinabili per appartenenza. Quindi il secondo insieme deve essere un insieme che quantomeno contiene ∅. Il secondo elemento.

Il secondo elemento non può contenere un elemento β diverso da ∅ perché per la transitività, questo implicherebbe che tale secondo elemento sia anche un sottoinsieme dell'ordinale: β dovrebbe essere un elemento dell'ordinale diverso da ∅ e questo non è possibile, perché l'insieme vuoto e β non sono ordinabili per appartenenza.

la definizione della successione degli ordinali. il superamento di omega. le tre operazioni che consentono di arrivare ad infiniti di cardinalità superiore.

back to index

Ma per quanti numeri successori si aggiungano alla serie, non si riesce, tramite la sola definizione di successore, ad arrivare ad un insieme di cardinalità infinita: per quanto tale successione proceda, non si riesce ad attingere al primo infinito, l'omega. Questo perché la successione 1, 2, 3, … conduce a numeri ciascuno più grande dei precedenti, ma pur sempre finiti.

Occorreva definire una successione di ordinali che andasse oltre quelli finiti e fosse esaustiva: in cui cioè tutti gli ordinali, nessuno escluso, compaiano ad un certo punto, secondo l'ordine di grandezza dato dall'inclusione (quello che i matematici chiamano lunghezza di un ordinale). Occorreva definire una seconda operazione, diversa da quella del passaggio al successore.

A questo scopo l'operazione di passaggio all'insieme potenza non può essere utilizzata, perché, mentre l'operazione successore produce un ordinale, l'operazione di passaggio da un ordinale al suo insieme delle parti non sempre produce un ordinale.

Consideriamo infatti il seguente passaggio dall'insieme A all'insieme delle parti P(A):

A = {∅, {∅}, {∅,{∅}}}

P(A) = {∅, {∅}, {∅,{∅}}, {∅, {∅}, {∅,{∅}}}, {∅, {∅,{∅}}}, {{∅}, {∅,{∅}}}}

Si può vedere che gli ultimi due elementi di P(A):

{∅, {∅,{∅}}}

{{∅}, {∅,{∅}}}

non fanno parte dell'ordinale successore di A né di qualsiasi altro ordinale.

Bisogna quindi definire una operazione diversa da P(A), che ci faccia rimanere all'interno della categoria degli ordinali e che fornisca l'ordinale precisamente successivo.

Per arrivare a omega occorre definire un diverso tipo di ordinale, l'ordinale limite, tramite una operazione di unione infinita. Omega rappresenta il limite della successione dei numeri naturali che si possono vedere all'interno delle parentesi graffe che sono il simbolo di insieme:

∪{1, 2, 3, …} = ω

Dato un insieme A, se la serie dei suoi elementi è finita e ha un massimo x allora si ha ∪A = x, cioè non viene prodotto nessun nuovo elemento oltre quelli contenuti in A. Se la serie degli elementi è infinita, ma non sono tutti ordinali, si produce un nuovo insieme, ma non necessariamente di cardinalità superiore a quella di A. Se la serie di elementi è infinita, ed è composta da ordinali, allora si produce un nuovo ordinale, di cardinalità superiore a quelli contenuti in A. E finalmente, se, in aggiunta, questa serie è data dagli ordinali successori di un dato ordinale, si ottiene precisamente un ordinale iniziale, cioè il primo di cardinalità superiore che segue la serie degli elementi di A.

Si sono così ottenuti ben tre metodi per creare insiemi di cardinalità superiore a partire da insiemi dati, finiti o infiniti: il passaggio al successore, l'unione generalizzata, il passaggio all'insieme potenza.

Mentre i primi due, a partire da un ordinale o da un insieme di ordinali, producono un ordinale, non così è per il terzo, come si è già detto.

In tal modo si giunge a quello che Cantor chiamò il primo aleph, l'infinito dei numeri naturali, ribattezzato col nome dell'ultima lettera dell'alfabeto greco: ω, omega.

Oltre l'omega la serie dei numeri ordinali prosegue tornando ad utilizzare la definizione di successore:

{ω, {ω}} : omega più uno, il primo passo sulla via degli infiniti superiori

{ω, {ω}, {ω, {ω}}} : omega più due

{ω, {ω}, {ω, {ω}}, {ω, {ω}, {ω, {ω}}}} : omega più tre

Si noti la semplicità delle leggi della numerazione: la serie degli omega è identica a quella dei numeri naturali, con l'unica variante che al posto di ∅ è ora ω:

{∅, {∅}, {∅, {∅}}, {∅, {∅}, {∅, {∅}}}, …}

{ω, {ω}, {ω, {ω}}, {ω, {ω}, {ω, {ω}}}, …}

Come si è già detto, i successori di omega sono tutti infiniti dello stesso tipo, nel senso che hanno tutti la stessa cardinalità.

Alternando l'operazione di successione con quella di unione infinita si può andare oltre la cardinalità di omega. Oltre la cardinalità di qualsiasi infinito. Ecco la definizione del primo infinito di cardinalità superiore ad omega:

∪{ω + n | n ∈ ω}

Si ottiene così una numerazione che va oltre i numeri naturali, la serie degli ordinali infiniti, come li chiamano i matematici. Quelli che utilizziamo nei calcoli di ogni giorno sono invece i cardinali finiti.

la "numerazione" mediante ordinali degli insiemi ben ordinati. la definizione di numero cardinale di frege. l'assioma di astrazione e i suoi paradossi. la definizione di cantor (in realtà di von neumann). l'ordinamento degli ordinali mediante inclusione o appartenenza. la definizione di cardinale come il minimo ordinale equipotente. gli aleph. la numerazione mediante cardinale degli ordinali.

back to index

Un qualsiasi insieme ben ordinato X può essere messo in corrispondenza bijettiva con uno e un solo ordinale Y mediante un isomorfismo f che mantiene l'ordine:

x₁ R_X x₂ ⇔ f(x₁) R_Y f(x₂)

In tal modo riusciamo a "numerare" qualsiasi insieme ben ordinato, assegnandogli il suo numero ordinale.

Gli insiemi numerati con i numeri ordinali differiscono tra loro o per la dimensione – cioè per il numero di elementi – o per l'ordine – cioè per il modo in cui sono disposti gli elementi. Due ordinali non sempre contrassegnano dimensioni diverse: potrebbero contrassegnare due ordini diversi entro insiemi della stessa dimensione.

se in omega è possibile porre sia la relazione "<" sia la relazione "≤", non abbiamo due ordini anziché uno? In base a quale dei due si definisce un ordinale?

back to index

[Go 165 ] Si supponga che R sia un ordine parziale debole su X e che la relazione S sia definita da:

xSy se e solo se xRy and x≠ y

Allora S è un ordine parziale stretto su X e se R è lineare anche S lo è.

[Go 165 ] Supponiamo viceversa che S sia un ordine stretto parziale su X, e che la relazione R sia definita da:

xRy se e solo se xSy or x = y

Allora R è un ordine parziale debole su X e se S è lineare lo è anche R.

[Go 165 ] Così, ciascun ordine debole su X è associato con un ordine stretto su X e viceversa. Questo significa che quando parliamo di un insieme X con un ordine lineare o parziale, possiamo indifferentemente riferirci alla forma debole o stretta dell'ordine, a seconda della convenienza.

[Go 165 ] Si tenga da ultimo presente una convenzione seguita dai matematici: un ordine stretto su X è espresso da "<" anziché ">" al posto di "R".

il buon ordine della classe degli ordinali

back to index

[Go 165,167] [En 192] La classe degli ordinali può essere ben ordinata da ∈, che è un ordine lineare stretto, cioè ha le seguenti caratteristiche:

▸ irriflessivo

▸ transitivo

▸ lineare (o tricotomia): due elementi sono comunque in relazione o sono uguali

▸ buon ordine: ogni insieme non vuoto contiene un least element

aritmetica ordinale

back to index

Cantor fu il primo ad utilizzare gli infiniti come oggetto di calcolo matematico e a mostrare che la loro aritmetica è completamente diversa da quella dei numeri finiti. Addizionò un numero finito ad un numero infinito: n + ω, e mostrò che il risultato esiste, ed equivale invariabilmente al secondo termine, ω:

n + ω = ω

per un numero n qualsiasi, e non solo per n = 0. Come dire che si ottiene a + b = a anche con addendi diversi da zero. Da questo derivano ulteriori paradossi:

1 + ω = 2 + ω = 3 + ω = …

Si ha anche:

ω + ω² = ω²

Si ha anche che, se ω² appartiene o è eguale ad α, e α² appartiene o è eguale a β, allora ω + β = β

Dalla relazione precedente si ricava, come caso particolare, che se ω² è incluso o eguale ad α, allora ω + α = α

non solo, ma è anche vero che:

1 + ω ≠ ω + 1

infatti si ha:

1 + ω = ∪{1 + γ | γ ∈ ω} = ω

ω + 1 = ω + 0⁺ = (ω + 0)⁺ = ω⁺ = ω ∪ {ω} ≠ ω

e risulta quindi violata anche la proprietà commutativa.

Inoltre, questo fa vedere che le ordinarie disequazioni non valgono, perché come conseguenza immediata otteniamo:

1 + ω < ω + 1

e in generale, se n è diverso da zero:

n + ω < ω + n

e anche queste sono espressioni che risulterebbero errate nel caso di numeri naturali

Non si può scrivere, neanche nel caso di α e β maggiori di zero:

α + β > β

ma:

α + β ≥ β

Per quanto riguarda la moltiplicazione, si ha:

n ⋅ ω = ω

per un numero naturale n qualsiasi, e non solamente per il numero n = 1, e si ha inoltre:

ω ⋅ ω = ω

La moltiplicazione è associativa ma non è commutativa:

2 ⋅ ω < ω ⋅ 2

infatti si ha:

2 ⋅ ω = ∪{2 ⋅ γ | γ ∈ ω} = ω

ω ⋅ 2 = ω ⋅ 1⁺ = (ω ⋅ 1) + ω = ω + ω

Esistono ancora numerose altre peculiarità:

Se 1 < h < k e k è infinito, allora 2^k = h^k

La moltiplicazione è distributiva a sinistra:

α ⋅ (β + γ) = α ⋅ β + α ⋅ γ

ma non è distributiva a destra:

(1 + 1) ⋅ ω ≠ 1 ⋅ ω + 1 ⋅ ω

infatti si ha:

(1 + 1) ⋅ ω = 2 ⋅ ω = ω

1 ⋅ ω + 1 ⋅ ω = ω + ω = ∪{ω + γ | γ ∈ ω}

e si ottiene quindi, invece dell'eguaglianza, una diseguaglianza:

(1 + 1) ⋅ ω < 1 ⋅ ω + 1 ⋅ ω

Per quanto riguarda la sottrazione si ha:

ω – n = ω

Inoltre, a differenza della sottrazione tra numeri relativi, che può essere effettuata sottraendo da un numero un numero ad esso maggiore, è impossibile definire la sottrazione tra un ordinale β e un ordinale α superiore nell'ordinamento degli ordinali (cioè che lo include).

Quanto all'elevazione a potenza, essa ha le usuali proprietà:

α² = α ⋅ α

α¹ = α

1^α = 1

α^β+γ = α^β ⋅ α^γ

(α^β)^γ = α^β^⋅^γ

ma non tutte:

(α + β)² ≠ α² + α ⋅ β + β ⋅ α + β²

2^ω = 3^ω = ω

(ω ⋅ 2)² ≠ ω² ⋅ 2²

L'aritmetica dei numeri infiniti si basa su definizioni rigorose. Ecco quelle di somma, sottrazione, moltiplicazione, divisione tra ordinali.

Somma tra ordinali:

α + 0 = α

α + β⁺ = (α + β)⁺

α + λ = ∪{α + γ | γ ∈ λ} nel caso λ sia un ordinale limite

Sottrazione tra ordinali:

dati due ordinali α ∈ β esiste un unico ordinale δ tale che α + δ = β, per cui si può scrivere:

α – β = δ

Come già detto, la sottrazione non è definita se il sottraendo è maggiore del minuendo (non è incluso nel minuendo).

Moltiplicazione tra ordinali:

α ⋅ 0 = 0

α ⋅ β⁺ = (α ⋅ β) + α

α ⋅ λ = ∪{α ⋅ γ | γ ∈ λ} nel caso λ sia un ordinale limite

Divisione tra ordinali:

Siano α e δ ordinali con δ (il divisore) diverso da zero. Allora esiste un'unica coppia di ordinali β e γ (quoziente e resto) tali che

α = δ ⋅ β + γ

Elevazione a potenza di ordinali:

α⁰ = 0⁺ = 1

α^β+ = (α^β) ⋅ α

α^λ = ∪{α^γ | γ ∈ λ} nel caso λ sia un ordinale limite

l'insieme ∪x di ordinali e cardinali

back to index

[Go 82] L'unione di un insieme o di una serie di insiemi viene stabilita da un apposito assioma (assioma dell'unione) nel sistema ZF:

∀x ∃y ∀z (z ∈ y ⇔ ∃w (z ∈ w & w ∈ x))

[Go 82] Scriviamo ∪X, chiamato "unione di un insieme" x, per indicare l'insieme che, in riferimento a tale assioma è definito come:

∀z (z ∈ y ⇔ ∃w (z ∈ w & w ∈ x))

[Go 209] Se X è un insieme di ordinali, ∪X è un ordinale, il minimo confine superiore ("least upper bound") di X.

[L 158] Se α è un insieme di ordinali, ∪α è un cardinale ed è il primo cardinale maggiore o uguale a tutti i cardinali in a; questo è ovvio se tra gli elementi di α c'è un massimo, che è allora ∪α. Se in α non c'è un massimo, già sappiamo che ∪α è un ordinale; dimostriamo che è un ordinale iniziale: supponiamo per assurdo che esista una bijezione tra ∪α e un β ∈ ∪α; allora esiste k ∈ α tale che β ∈ k e card(β) < k; la supposta bijezione, ristretta a k ⊆ ∪α, manderebbe k iniettivamente in un sottoinsieme di β di cardinalità strettamente minore di k, il che è impossibile. ∪α è il sup di α rispetto all'ordine tra cardinali, perché se k < ∪α, cioè k ∈ ∪α, allora k ∈ h ∈ α, e k non può essere un maggiorante di α.

l'induzione transfinita

back to index

Per questi insiemi infiniti superiori ad ω i matematici hanno definito un processo dimostrativo che corrisponde a quello della dimostrazione per induzione di una proprietà dei numeri naturali: il procedimento di induzione transfinita. Il procedimento di induzione ordinaria è invece quello già descritto dal terzo degli assiomi di Peano:

Se un qualsiasi sottoinsieme A dell'insieme dei numeri naturali ℕ contiene l'elemento 0 e contiene S(x), cioè il successore di x ogniqualvolta x appartenga ad A, allora A coincide con ℕ.

La formulazione in termini insiemistici rende difficile capire che in realtà questo è un procedimento per dimostrare proprietà dei numeri naturali. L'insieme A viene in partenza definito in base ad una proprietà. In tal modo, il principio di induzione permette di estendere ai numeri naturali una proprietà laddove sembra che estenda semplicemente l'appartenenza ad A. Questo perché, in termini di teoria degli insiemi, una proprietà P goduta dagli elementi dell'insieme X non è altro che un sottoinsieme di X: precisamente quello che contiene tutti e soli gli elementi che godono della proprietà. I matematici parlano sinteticamente di "proprietà A".

Ecco il principio di induzione transfinita, che consente di estendere una proprietà non solo ad elementi di insiemi con la cardinalità di omega, ma agli elementi appartenenti ad ordinali infiniti di cardinalità superiore:

Sia A un sottoinsieme dell'ordinale α, tale che siano verificate le due proprietà:

(i) 0 ∈ A

(ii) per tutti gli ordinali β appartenenti ad α, se β è incluso in A allora β appartiene ad A

Allora A = α

rapporti degli ordinali con gli altri insiemi

back to index

[En 195] (Teorema di Hartog) Dato un qualsiasi insieme A, esiste un ordinale α che non è dominato da A, cioè tale che α ⋠ A. Un simile ordinale può essere definito come:

α = {β | β è un ordinale & β ≼ A}

la successione degli ordinali

back to index

[Go 251] Ecco la successione degli ordinali:

1,2,3,…, ω

ω + 1, ω + 2, ω + 3, …, ω + ω = 2ω

ω, ω + ω, ω + ω + ω, … = 1ω, 2ω, 3ω, …

∪{1ω, 2ω, 3ω, …} = ω ⋅ ω = ω²

(ω ⋅ ω) + 1, …, (ω ⋅ ω) + (ω ⋅ ω) = 2(ω ⋅ ω)

1(ω ⋅ ω), 2(ω ⋅ ω), 3(ω ⋅ ω), …, ω ⋅ ω ⋅ ω = ω³

∪{ω, ω², ω³, …} = ω^ω

ω^ω + ω^ω = 2ω^ω, 3ω^ω, ω ⋅ ω^ω, …, ω^ω ⋅ ω^ω = (ω^ω)², …, (ω^ω)^ω

(ω^ω)^ω = ω^ω², ω^ω³, …,

, , …

∪{, , , …} = ε₀

[Go 251, 252] Si può dimostrare che ε₀ è contabile, e quindi che ε₀ <ω₁; quest'ultimo, lo si ricordi ([Go 215]) è il minimo ordinale non-contabile (least uncountable ordinal), dato da:

ω₁ = {α | α è un ordinale contabile}

Ciò è fondamentalmente dovuto al fatto che qualsiasi unione contabile di insiemi contabili è contabile.

il paradosso di burali-forti

back to index

[En 194] Si può dimostrare che la classe di tutti gli ordinali è una classe transitiva ben-ordinata dalla relazione di appartenenza. Se fosse un insieme, allora avrebbe tutte le caratteristiche di un ordinale. Ma sarebbe un membro di se stesso, e nessun ordinale ha questa proprietà.

le varie forme dell'assioma di scelta. prova che ac implica wo.

back to index

L'assioma di scelta può assumere molte forme equivalenti:

▸ [Go 108] Data una famiglia F di insiemi non-vuoti, esiste una funzione h : F ➙ ∪F tale che per ogni A ∈ F si ha che h(A) ∈ A. Questa funzione h è chiamata funzione di scelta (cosiddetta choice function) per F.

▸ [Go 108] Si supponga che F è una famiglia di insiemi disgiunti e non vuoti, cioè tali che per due distinti insiemi A,B ∈ F, A ∩ B = ∅. Allora c'è una funzione h : F ➙ ∪F tale che per ogni A ∈ F h(A) ∈ A.

▸ [Go 108] Per ogni insieme non vuoto M c'è una funzione dagli elementi del suo insieme potenza (escluso l'insieme vuoto) in M tale che l'immagine del sottoinsieme A di M appartenga ad A

▸ Ogni insieme può essere ben ordinato

▸ (Lemma di Zorn): Sia P un insieme non vuoto ordinato dalla relazione R, tale che ogni catena⁽⁹⁾ C in P abbia un confine superiore⁽¹⁰⁾ in P. Allora P contiene almeno un elemento massimale⁽¹¹⁾.

Ma questo assioma assume forme ancora più specifiche, come le seguenti, che non sono puramente conseguenze, ma equivalenti dell'assioma:

▸ [Go 116] (Teorema di Tychonoff) Il prodotto infinito di spazi compatti è compatto

▸ [Go 116] (Teorema di completezza) Dato un linguaggio infinito del primo ordine, un insieme di formule è coerente se e solo se ha un modello.

▸ [Go 138] (Principio dicotomico) Per due qualsiasi insiemi A e B si ha che A ≼ B oppure B ≼ A

▸ [En 151] Per ogni relazione R c'è una funzione f ⊆ R con dominio eguale a quello di R

▸ [En 151] (Assioma di moltiplicazione) Il prodotto cartesiano di insiemi non vuoti è sempre non vuoto

▸ [En 151] Sia A un insieme tale che (a) ogni membro di A è un insieme non vuoto e (b) due qualsiasi membri distinti di A sono disgiunti. Allora esiste un insieme C che contiene esattamente un elemento da ciascun membro di A

Le forme principali dell'assioma vengono abbreviate in AC (assioma di scelta), WO (principio del buon ordine), ZL (lemma di Zorn)

Prova che AC implica WO (data una funzione di scelta un insieme può essere ben-ordinato). [Go 265] AC implica WO

Dopo aver scelto un ordinale α più grande di X tramite Hartog, utilizziamo AC per costruire una funzione suriettiva α ➙ X nel seguente modo:

data una choice function h : P(X)\∅ ➙ X tale che h(A) ∈ A per ogni A ⊆ X e un insieme c non contenuto in X definiamo:

f : α ➙ X ∪ X

0 ↦ h(X)

β ↦ h(X\Range(f|_β)) se X\Range(f|_β) ≠ ∅

β ↦ c se X\Range(f|_β) = ∅

(per capire perché l'immagine di β è X\Range(f|_β)) e non X\Range(f|_β–)) occorre tenere conto che β = {β^–})

Si può mostrare che se f(γ) e f(λ) sono in X (cioè non hanno immagine c) allora è f(γ) ≠ f(λ)

Si può mostrare che, dato Hartog e l'affermazione precedente, c deve essere in Range(f), cioè che ci deve essere una "eccedenza" di α su X

Sia δ il least element delle controimmagini di c

Si può mostrare che f|_δ è una bijezione δ ➙ X

Si può sfruttare questa bijezione per dotare X di un well-order

cosa si può provare con ac e cosa non si può provare senza ac. risultati che si è scoperto derivare dall'assioma di scelta. paradossi che derivano dall'assioma di scelta e perplessità al suo riguardo.

back to index

Senza AC non si può stabilire una bijezione tra ℕ e un insieme numerabile

[Go 149] Senza AC non si può stabilire una bijezione tra ℕ e un insieme numerabile (cioè contabilmente infinito) X, perché in generale ci saranno diverse bijezioni tra ℕ e X, e abbiamo la necessità di sceglierne una. Se X ha una sufficiente struttura, ci potrebbe essere un modo di specificare la bijezione. Ma altrimenti è richiesta una forma di AC.

Senza AC non si può dimostrare il converso dell'affermazione che se ℕ ≼ X allora X è infinito

[Go 149] Senza AC si può dimostrare che se ℕ ≼ X allora X è infinito. Ma senza AC non si può dimostrare il converso, perché X non ha sufficiente struttura per definire una iniezione da ℕ ad X.

Con AC si può assegnare un cardinale ad ogni insieme infinito

[Go 268] Con AC si può assegnare un numero cardinale ad ogni insieme infinito

Se A ⋠ B, senza AC non si può concludere che B ≺ A.

[Go 255] Se A ⋠ B, senza AC non si può concludere che B ≺ A. Infatti, è lo stesso problema dell'assioma di scelta: posto che A ➙ B sia suriettiva, come scegliere una controimmagine per ogni elemento di B?

Con AC si può dimostrare che l'unione contabile di insiemi nulli è nulla

[Go 113] Un risultato classico della teoria dell'integrazione di Lebesgue è che una unione contabile di insiemi nulli è nulla. Un sottoinsieme X di ℝ è nullo se per ogni dato ε > 0 c'è una sequenza <I_n> di intervalli che copre X con lunghezza totale inferiore ad ε, cioè X ⊆ ∪{I_n | n ∈ ℕ} e ∑_n_∈_ℕ l(I_n) < ε

[Go 114] Un'altra conseguenza dell'assioma di scelta si ha nella teoria della misura di Lebesgue, e consiste nel fatto che esistono sottoinsiemi non-misurabili degli spazi ℝⁿ.

[Go 114] Il concetto di misura su un sottoinsieme di ℝⁿ generalizza la nostra intuizione della lunghezza di un intervallo di ℝ o di una curva in ℝ², dell'area di una superficie delimitata da un profilo in ℝ² e del volume di un solido in ℝ³. Nella teoria di Lebesgue una misura è una funzione μ da qualche insieme Y di sottoinsiemi di ℝⁿ in ℝ ∪ {∞} con le seguenti proprietà:

(i) μ(X) ≥ 0

(ii) se X e Y sono sottoinsiemi congruenti di ℝⁿ allofa μ(X) = μ(Y)

(iii) μ è contabilmente additivo, cioè, se X₀, X₁, X₂, …, X_n, … sono un numero contabile di insiemi disgiunti di ℝⁿ allora

Normalmente si impone un qualche tipo di unità di misura per una specifica misura: per esempio, per misurare lunghezze di sottoinsiemi della linea reale ℝ, si definisce normalmente la misura dell'intervallo chiuso unitario μ([0,1]) = 1 e la misura di un intervallo [a,b] come b – a. Gli insiemi nulli sono gli insiemi con misura zero. La misura di ℝ è posta pari ad ∞.

Utilizzando l'assioma di scelta il quesito se tutti i sottoinsiemi di ℝⁿ possiedono una misura ha risposta negativa. Come conseguenza di AC si ricava, più precisamente, che esiste un sottoinsieme del cerchio unitario C che ha una lunghezza non-misurabile. Questo teorema è facilmente estendibile al disco unitario in R².

Il paradosso di Tarski

[Go 116] AC dà luogo al paradosso di Tarski: Sia S la sfera solida unitaria in ℝ³, cioè l'insieme di tutti i punti compresi nella sfera di raggio unitario. Allora S può essere sottoposto a partizione in un numero finito di sottoinsiemi che possono essere spostati, usando traslazioni e rotazioni, per produrre due sfere solide unitarie. Questo teorema è spesso descritto come un paradosso.

[Go 117] Ma in realtà AC ha talmente tante conseguenze ragionevoli che sembra desiderabile accettarlo come una parte non contestabile della matematica.

Le conseguenze principali di AC sotto forma di lemma di Zorn

[Go 121 ss.] Ogni gruppo ha un sottogruppo abeliano, cioè in cui l'addizione è commutativa

[Go 121 ss.] Ogni spazio vettoriale ha una base

[Go 121 ss.] Dati due insiemi A e B esiste una funzione iniettiva da A a B o da B ad A

Senza AC non si può provare che una funzione possiede un'inversa

[Go 104] Supponiamo che f : A ➙ B sia una funzione suriettiva. Esiste una funzione iniettiva g : B ➙ A tale che f(g(b)) = b per tutti gli b ∈ B? Il problema è scegliere una delle controimmagini di ciascun b ∈ f^–1(B). Se fosse B = ℕ potremmo sfruttare il buon ordine di ℕ e scegliere il least element. Ma già con ℝ non possiamo usare tale soluzione, perché un sottoinsieme non vuoto di ℝ non contiene necessariamente un elemento minimo (least element). Non c'è modo di trovare una funzione g con gli assiomi di ZF. Solo in alcuni casi il problema può essere risolto: es. quando f : ℝ ➙ ℝ è continua e non-decrescente

[Go 106] Se si ha f : ℝ ➙ B con B finito si può sempre dare una lista finita di valori di g(f(b)), uno per ogni elemento b di B.

[Go 106] Se B è finito non c'è problema nel descrivere g. Ma se B è infinito, abbiamo bisogno di informazioni aggiuntive su A o su entrambi, per assicurare che possiamo descrivere g. E se non possiamo descrivere g in modo diverso se non stabilendo per assioma la proprietà desiderata di tale g (cioè che f(g(b)) = b per ogni b) su quale base possiamo asserire che g esiste? E' per risolvere questo problema che viene introdotto l'assioma di scelta.

[Go 107] Bertrand Russell diede una divertente illustrazione dell'uso dell'assioma di scelta. Pensate a come si può descrivere il modo di scegliere una scarpa da ciascun paio di una infinita serie di paia. Per "descrizione" intendiamo qualcosa che può essere comunicato ad altre persone e usato da queste in modo che ciascuna persona prenderebbe la stessa scarpa da ogni paio. Si tratta di applicare una funzione di scelta, come definita sopra, non una istruzione del tipo: "prendi una scarpa a caso da ogni paio". Potremmo specificare la funzione di scelta nel seguente modo: "Scegli sempre la scarpa sinistra". Ora proviamo a fare la stessa cosa per un insieme infinito di paia di calzini. A differenza del caso precedente non c'è una descrizione finita di una funzione di scelta. Si potrebbe applicare un contrassegno ad uno del calzini di ogni paio, ma la teoria degli insiemi richiede una descrizione finita. L'assioma di scelta dice semplicemente che esiste una funzione di scelta, che viene evocata dal nulla!

ac, sotto forma di funzione di scelta, consente di dare ad ogni insieme un buon ordinamento.

back to index

Dimostrazione di Enderton che grazie all'assioma di scelta un qualsiasi insieme può essere ben ordinato.

Con l'assioma di scelta si può definire un buon ordinamento su qualsiasi insieme A. Il teorema di Hartog garantisce che per ogni insieme A ci sia un ordinale α che non è dominato da A. Questo ci consente di disporre di un ordinale α per tentare di stabilire una funzione iniettiva α ➙ A senza il rischio che gli elementi di α si esauriscano. Ma senza l'assioma di scelta ci dovremmo fermare a questo punto, perché dal fatto che α ⋠ A non possiamo concludere che A ≺ α, cioè che vi è una funzione iniettiva da A in α. Per ottenere questa funzione iniettiva dobbiamo far uso dell'assioma di scelta, nella forma della choice function: per ogni insieme A c'è una funzione di scelta F : P(A) ➙ A tale che F(B) ∈ B per ogni subset non vuoto B di A.

Abbiamo anche bisogno dello Schema di Teorema di Ricorsione Transfinita: Si assuma che esista un buon ordine > su un insieme A. Data una qualsiasi formula φ(f,y) che lega una funzione f con dominio A ad un insieme y, tale che per ogni f esista un solo y tale che φ(f,y), allora esiste una funzione F con dominio A tale che φ(F|_{seg t} , F(t)).

[En 176] La formula φ non è in realtà che una class function, cioè una classe di coppie ordinate, dall'insieme ^>AV di tutte le funzioni dai segmenti iniziali di un insieme A verso un qualsivoglia altro dominio (V è la classe universale), che consente di definire univocamente la funzione F(t) = G(F|_{seg t}). Ma quest'ultima formula non è consentita in ZF, perché G è una classe e non sono ammesse classi. Così occorre riformulare G, come si è fatto, utilizzando una formula φ.

[En 177] In particolare, se φ(f,y) è: "rango(f) = y" otteniamo il seguente teorema: Si assuma che < è un buon ordine su A. Allora esiste un'unica funzione con dominio A tale che F(t) = rango(F|_{seg t}).

[En 196] Sia dato un oggetto e che non appartiene ad A e una funzione di scelta G : P(A) ➙ A. Usiamo la ricorsione transfinita per ottenere una funzione F : α ➙ A ∪ e tale che per ogni γ ∈ α si ha:

▸ F(γ) = G(A – F[[γ]]) se A – F[[γ]] ≠ ∅

▸ F(γ) = e se A – F[[γ]] = ∅

dove F[[γ]] = rango(F|_γ)

In altre parole, F(γ) è un membro scelto di A – F[[γ]]

Il primo elemento di α è ∅, e quindi F(∅) = G(A – F[[∅]]) = G(A – ∅) = G(A)

Poiché ogni elemento δ di un ordinale include in sé il segmento iniziale seg δ secondo l'ordine ∈, col procedimento sopra indicato non c'è pericolo che la sua immagine coincida con una delle immagini degli ordinali che esso contiene.

Una volta stabilita l'iniezione α ➙ A, l'ordine è dato dalla stessa iniezione: f(β) < f(λ) in A sse β ∈ λ in α.

[En 197] Si può dimostrare che si tratta di un isomorfismo d'ordine (order-isomorphism) tra A e il segmento iniziale di α.

E' possibile dimostrare che l'iniezione è tra A e il segmento iniziale di α. Si consideri infatti una funzione F tra l'ordinale 10 = {1,2,3,4,5,6,7,8,9} e l'insieme A = {a, b, c d, e}, che ha cinque elementi. Se prendiamo 9, la sua immagine deve cadere in A – F[[{1,2,3,4,5,6,7,8}]], e quindi sicuramente cadere in e. Lo stesso vale per l'immagine di 8,7,6. Quindi la bijezione si instaura solo col segmento iniziale {1,2,3,4,5}.

In che modo interviene il teorema di ricorsione transfinita nel modellare la funzione F? La formula φ(F,y) diviene: "y = G(A – F[[γ]])"

[En 178 riga 4] Perché il teorema funzioni è necessario anche l'assioma di rimpiazzamento. Tale assioma viene utilizzato fondamentalmente per dimostrare che, data una class function H su un insieme A, che H[[A]], immagine di A in H, è un insieme. Nel caso di una ordinaria set-function (funzione che è un insieme) il fatto che rango(A) è un insieme è provabile in base agli altri assiomi.

i cardinali

back to index

[En 197] Il teorema del buon ordinamento (ogni insieme può essere ben ordinato ed è collegato da un isomorfismo d'ordine al segmento iniziale di un qualche ordinale) consente di concludere che ogni insieme è equinumeroso con qualche numero ordinale.

[En 197] Il numero cardinale di un insieme A, indicato con card(A), è il più piccolo ordinale equinumeroso con A.

[Ho 42] In alternativa, possiamo dire che un numero cardinale è un ordinale che non può essere messo in corrispondenza bijettiva con un ordinale più piccolo.

[Lo 157] Gli ordinali finiti sono cardinali; ω è un cardinale; ω⁺ non lo è. In generale se α è un ordinale infinito, α⁺ non è un ordinale.

Un cardinale non è altro che un ordinale iniziale. [En 199] Diciamo che un ordinale è un ordinale iniziale se e solo se non è equinumeroso con nessun ordinale più piccolo. Allora ogni ordinale iniziale è anche il proprio numero cardinale. Di converso, qualsiasi numero cardinale deve, per definizione, essere un ordinale iniziale. Così vediamo che cardinali e ordinali iniziali sono esattamente la stessa cosa.

nozioni da leggere prima di studiare i cardinali

back to index

▸ Ci sono dei simboli, come 2^ω, che indicano una cardinalità ben definita, ma non sono cardinali, perché i cardinali devono essere insiemi ordinali. Tenere presente che ω⁺ è un ordinale, mentre ω + 1 non è un ordinale, pur avendo la stessa cardinalità, e anche lo stesso ordine.

▸ Alcuni autori, come Lolli, introducono usano, accanto a Card(A), che è il cardinale vero e proprio, anche card(A), che è invece un simbolo che va letto nel contesto di espressioni di confronto, come "card(A) = card(B)" che esprimono solo relazioni di equinumerosità o iniettività.

▸ ℝ è sicuramente equipotente a numerosi ordinali con ordini diversi, ma in genere gli studiosi non sanno indicare di che tipi di ordini si tratti. Tanto meno sanno indicare, tra tutti gli ordinali equipotenti ad ℝ, il cardinale (ordinale) corrispondente ad ℝ. Ci si limita a dire che ℝ ≈ 2^ℕ, ma 2^ℕ non è neanche un ordinale.

le relazioni di equipotenza tra insiemi e l'esplorazione delle dimensioni dei principali insiemi

back to index

Cantor dimostrò una cosa che nessuno prima di allora aveva dimostrato: che esistono infiniti di tipo differente. Che oltre l'infinito dei numeri naturali esiste l'infinito dei numeri reali, e oltre quello innumerevoli e diversi altri, senza fine.

In matematica, spesso, la formulazione esatta di un problema è più importante della soluzione. Egli si chiese: cosa esattamente vuol dire che un insieme infinito è più grande di un altro? Provò a ribaltare la domanda, e si chiese: in che modo possiamo verificare che due insiemi infiniti hanno la stessa dimensione? La risposta venne allora con chiarezza: quando è possibile trovare una bijezione tra di essi. In tal caso si dice che hanno la stessa cardinalità o che sono equipotenti o aventi la stessa potenza. Un insieme equipotente a quello dei numeri naturali è detto numerabile.

Armato di questo criterio, Cantor passò al setaccio gli insiemi noti per confrontarne le dimensioni.

Emersero subito i primi apparenti paradossi: l'insieme dei numeri naturali è equipotente a quello dei soli numeri naturali pari: infatti, è possibile dare la seguente legge:

f(n) = 2n

che stabilisce una corrispondenza biunivoca tra i due insiemi, provando che essi hanno la stessa dimensione. Una bijezione collega pure i naturali con i naturali dispari.

Cantor indicò col simbolo "≈" la relazione di equipotenza e col simbolo "≼" la relazione che collega l'insieme di sinistra con quello di destra mediante una bijezione ovvero una iniezione.

Indicò col simbolo "≺" la relazione che collega l'insieme di sinistra con quello di destra mediante una iniezione che non è una bijezione.

Esplorò l'argomento delle relazioni di equipotenza tra i vari insiemi numerici.

Scoprì che l'insieme dei numeri interi e, inaspettatamente, quello dei numeri razionali, cioè dei numeri decimali finiti o periodici, sono equipotenti ai numeri naturali.

I numeri irrazionali – cioè tutti i decimali non finiti e non periodici – non sono commensurabili con i numeri naturali, hanno una dimensione superiore, la cardinalità del continuo: sono equipotenti ai punti della retta reale. La dimostrazione di Cantor è rimasta famosa col nome di dimostrazione diagonale⁽³⁾.

Scoprì anche che l'insieme dei numeri reali può essere messo in corrispondenza biunivoca con un suo qualsiasi sottoinsieme aperto, come quello compreso tra gli estremi zero ed uno esclusi.

Ecco, di seguito, un elenco dei più importanti risultati conseguiti da Cantor:

P(X) ≈ 2^X : L'insieme delle parti di X è equipotente all'insieme di tutte le funzioni da X nell'insieme {0,1} = 2

Dato un qualsiasi insieme X si ha che X ≺ P(X) : X può essere messo in corrispondenza bijettiva con un sottoinsieme proprio di P(X), ma non con l'intero P(X)

ℚ ≈ ℕ : l'insieme dei numeri razionali è equipotente a quello dei numeri naturali (vedine in nota la dimostrazione)⁽⁴⁾

ℕ ≈ ℤ : l'insieme dei numeri naturali è equipotente all'insieme dei numeri interi (naturali positivi e negativi)

ℕ ≺ ℝ : vale a dire che ℝ è non-contabile (contabile è un insieme che è finito o numerabile, cioè equipotente ad ℕ)

ℝ ≈ P(ℚ) ≈ 2^ℕ : l'insieme dei numeri reali è equipotente all'insieme delle parti dei numeri razionali e all'insieme delle funzioni dall'insieme dei numeri naturali nell'insieme {0,1} = 2

ℕxℕ ≈ ℕ : il prodotto cartesiano dato da tutte le coppie composte da numeri di ℕ è equipotente ad ℕ

ℕ ≺ ℝ\ℚ : l'insieme dei numeri irrazionali ℝ\ℚ è non-contabile

(–1,1) ≈ ℝ : l'insieme dei numeri reali ℝ è equipotente all'intervallo aperto di estremi –1, 1

(x,y) ≈ ℝ : l'insieme dei numeri reali ℝ è equipotente ad un qualsiasi intervallo aperto (con x < y)

{ℕⁿ | n ∈ ℕ} ≈ ℕ : l'insieme di tutte le sequenze di numeri naturali è equipotente ad ℕ

L'insieme dei numeri algebrici, cioè l'insieme dei numeri che sono soluzioni delle equazioni algebriche:

a₀xⁿ + a₁x^n–1 + … + a_n = 0

dove gli a_i sono interi, è numerabile

I numeri trascendenti, cioè non-algebrici (tra cui vi sono il numero di Eulero e e π) sono equipotenti ad ℝ

gli infiniti di cardinalità superiore a quella dei reali e l'ipotesi (generalizzata) del continuo

back to index

Esistono altri infiniti, di cardinalità superiore a quella dei numeri reali?

La dimostrazione è in realtà semplice: esiste un'operazione insiemistica ben nota, che da un insieme A produce un altro insieme, denotato con P(A) e chiamato insieme delle parti di A, o insieme potenza di A che comprende tutti i sottoinsiemi di A (incluso A stesso). Cantor provò che ogni volta che si passa da un insieme all'insieme delle parti la cardinalità aumenta, e che questo processo può essere ripetuto un numero illimitato di volte:

P(A)

P(P(A))

P(P(P(A)))

……………

Ogni volta si ottiene un infinito di dimensione superiore.

Cantor si pose il problema dell'immediato successore di ℝ, l'insieme dei numeri reali: tra ℝ e P(ℝ) esiste un infinito di dimensione intermedia, o i salti avvengono da un insieme all'insieme delle parti senza tappe intermedie? Fece la congettura che gli insiemi intermedi non esistano. E' nota come ipotesi generalizzata del continuo o GCH. La congettura limitata agli insiemi ℝ e P(ℝ) è nota come CH.

Nel 1940 Kurt Gödel provò che se ZF è coerente, lo è pure ZF con CH e GCH.

Nel 1963 Paul Cohen mostrò che se ZF è coerente, AC, CH e GCH non possono provate a partire dai suoi assiomi (AC è l'assioma di scelta, di cui parleremo in seguito). GCH non può essere provato neanche in ZFC, cioè aggiungendo a ZF l'assioma di scelta.

i numeri cardinali. la definizione di numero cardinale di frege. l'assioma di astrazione e i suoi paradossi. la definizione di cantor (in realtà di von neumann). l'ordinamento degli ordinali mediante inclusione o appartenenza. la definizione di cardinale come il minimo ordinale equipotente. gli aleph. la numerazione mediante cardinali degli ordinali.

back to index

Il passo successivo consiste nel creare, come naturale sviluppo della nozione di equipotenza, una seconda serie di numeri, che contrassegna esclusivamente la dimensione di ciascun insieme infinito. Questa seconda numerazione è quella dei numeri cardinali.

Prima di Cantor, esisteva già una definizione di tali numeri, data da Gottlob Frege: un numero cardinale è un insieme di tutti gli insiemi equipotenti. Il numero 4 è l'insieme di tutti gli insiemi che possiedono quattro elementi. Il numero 5 è l'insieme di tutti gli insiemi con cinque elementi. E così via⁽⁸⁾. La grande eleganza della definizione di Frege nascondeva però gravi paradossi, che furono scoperti pochi anni più tardi.

Consideriamo il seguente paradosso: se 1 è l'insieme di tutti gli insiemi con un elemento, possiamo formare un nuovo insieme che contenga 1, e cioè {1}. Questo insieme include 1, ma al contempo 1 è incluso in esso:

1 ∈ {1} ∈ 1

Ma la pecca logica fatale della definizione di Frege era molto più sottile e molto più grave. Il sogno di Frege era di ridurre la matematica all'insiemistica e l'insiemistica alla logica. Questo indirizzo di pensiero viene chiamato logicismo. Per ridurre la teoria degli insiemi alla logica, Frege stabilì una corrispondenza tra ciascuna delle proprietà predicabili di un qualsiasi oggetto e un insieme. Se la proprietà P è predicabile degli oggetti a, b, c, d e di nessun altro, allora essa corrisponde all'insieme {a,b,c,d}. Viceversa, possiamo descrivere un insieme fornendo la proprietà che hanno i suoi elementi e nessun altro. Questo metodo di descrivere insiemi è molto potente, e viene detto principio di astrazione:

{x | x è rosso}

è l'insieme degli oggetti rossi

{x | x è umano e x è nato in Inghilterra}

definisce l'insieme di tutti gli inglesi (secondo una possibile definizione di questo popolo). E così via.

E' proprio questo metodo che è stato usato da Frege per costruire i suoi numeri naturali: uno è l'insieme i cui elementi hanno la proprietà di essere insiemi e di avere un solo elemento:

{x | x è un insieme e x possiede un solo elemento}

due è l'insieme i cui elementi hanno la proprietà di essere insiemi e di possedere due elementi:

{x | x è un insieme e x possiede due elementi}

e così via.

Ma proprio questo modo di definire insiemi nasconde paradossi. Prendiamo ad esempio l'insieme V di tutti gli insiemi. Allora V deve appartenere a se stesso: V ∈ V. Questo contraddice la nostra idea intuitiva di un insieme come collezione di oggetti materiali che, in quanto tale, non può appartenere a se stessa.

Ma il paradosso più grave, noto come paradosso di Russell, è il seguente. Consideriamo l'insieme S di tutti gli insiemi che non appartengono a se stessi. Chiediamoci: S appartiene a se stesso? Se diciamo che S appartiene a se stesso, allora S non può appartenere a se stesso, perché gli appartengono solo gli insiemi che non appartengono a se stessi. Se diciamo che S non appartiene a se stesso, allora S appartiene a se stesso, perché in tale insieme sono compresi proprio gli insiemi che non appartengono a se stessi. Quale che sia l'affermazione su S, essa genera una contraddizione con altre affermazioni che abbiamo fatto su S.

Pertanto, non può essere utilizzato, per fondare la teoria degli insiemi, un assioma del tipo:

∃y ∀x (x ∈ y ⇔ φ(x))

Quando Cantor si mise all'opera, una definizione soddisfacente di numero cardinale che sostituisse quella di Frege non era stata ancora trovata.

[Go 128] Cantor è il creatore della teoria dei cardinali infiniti.

L'idea alla base della moderna definizione insiemistica di cardinale è di prendere un ordinale da ciascun gruppo di ordinali equipotenti e definirlo come il numero cardinale di tutti quelli e degli altri insiemi non-ordinali equipotenti. Di ciascun gruppo di ordinali equipotenti si prende il più piccolo. [Go 268] Questo ha il vantaggio che un cardinale è un insieme, non una classe propria, come sarebbe se fosse definito al modo di Frege.

[Go 268] (Effettivamente la definizione di Cantor era nella scia di quella di Frege: egli definiva il cardinale di un insieme X come l'insieme {Y | Y ≈ X} di tutti gli insiemi equipotenti ad X).

Ma occorre chiarire il concetto di più piccolo, introducendo una nuova relazione di ordine lineare tra gli ordinali. Come già rilevato, tra le notevoli proprietà dei numeri ordinali c'è quella che essi sono transitivi. Un insieme transitivo è un insieme A ciascun elemento del quale è anche un insieme contenuto in esso:

a ∈ A ➙ a ⊆ A

La relazione di appartenenza di un ordinale ad un altro, maggiore, come suo elemento, è la relazione idonea a definire un ordine. In realtà, poiché due ordinali sono in relazione di inclusione se e solo se sono anche in relazione di appartenenza, avrei potuto usare indifferentemente anche la relazione di inclusione.

Cantor si imbatté qui in un apparente paradosso, che non sfuggì ai suoi critici: come era possibile, che un insieme incluso in un altro, addirittura elemento di esso potesse avere lo stesso numero di elementi?

Ma in realtà non c'è niente di nuovo: l'intervallo di numeri compresi tra zero ed uno esclusi appartiene ed è incluso nell'insieme ℝ dei numeri reali, e tuttavia è equipotente ad esso. Anzi, una caratteristica di quasi tutti gli insiemi infiniti è di essere equipotenti ad un sottoinsieme proprio. Questa caratteristica è così comune che in effetti è uno dei criteri utilizzati per dimostrare che un insieme è infinito.

Definizione di numero cardinale. Un numero cardinale, dunque, è il minimo ordinale di un gruppo di ordinali equipotenti. Il numero cardinale ha la proprietà di essere un ordinale iniziale: non è equipotente a nessun sottoinsieme proprio. Cardinali e ordinali iniziali coincidono. I cardinali infiniti, come vedremo più avanti, sono gli aleph.

[Go 259] In realtà tutti gli aleph sono anche ordinali limite, per la semplice ragione che se fossero ordinali successori sarebbero equipotenti all'ordinale che li precede, e che è un loro sottoinsieme proprio.

E con questo rimangono definite tre categorie, che esauriscono tutti i tipi di ordinali: gli ordinali successori, gli ordinali limite (quelli ottenuti con le unioni infinite di successori), e gli ordinali iniziali.

la numerazione mediante cardinali degli ordinali. la numerazione mediante cardinali degli insiemi ben ordinati. la numerazione mediante cardinali degli insiemi non ben ordinati. il ruolo dell'assioma di scelta. come si può creare una choice function in un insieme ordinato con wo.

back to index

I cardinali finiti coincidono con gli ordinali, perché la classe di ordinali equipotenti al numero n è formata dal solo n. Invece i cardinali infiniti sono equipotenti a più ordinali infiniti.

Definendo un cardinale come il minimo ordinale di un gruppo di ordinali equipotenti si riesce ad assegnare un numero cardinale ad essi, e quindi ad assegnare un cardinale ad ogni ordinale.

Dimostrazione che se un insieme X ha un buon ordine può essergli assegnato un cardinale (aleph) E' anche possibile assegnare un numero cardinale ad un insieme infinito, a patto che questo sia ben ordinabile. [Go 259, 268] Se X è un qualsiasi insieme infinito dotato di un buon ordine, esso sarà collegato da un isomorfismo d'ordine ad un dato ordinale α. Tra gli ordinali equipotenti ad α esiste un ordinale iniziale ℵ_γ, che è anche il più piccolo ordinale tra essi. Poiché X è equipotente ad α che a sua volta è equipotente a ℵ_γ si ha che X ≈ ℵ_γ.

Per inciso, se un insieme infinito ha un buon ordine allora può essere dotato di tutti i buoni ordini corrispondenti ai vari ordinali equipotenti. Questo perché questo insieme è collegabile a qualsiasi ordinale equipotente tramite bijezione, e mediante tale bijezione può essergli imposto l'ordine dell'ordinale.

Non è però possibile assegnare un cardinale ad un insieme che non sia ben-ordinabile.

[Go 190] Per lungo tempo, ad esempio, i matematici, tra cui David Hilbert, si sono chiesti se possa essere dato un buon ordine ad ℝ. Questo buon ordine, se esiste, deve essere diverso dall'usuale ordine "<", perché ℝ, ordinato in questo modo, non possiede buon ordine.

Se non sappiamo nulla circa l'esistenza del buon ordine in un insieme infinito, non possiamo assegnargli un cardinale. E' necessario postulare il suo buon ordine tramite uno specifico assioma, l'assioma di scelta, che, in una delle sue forme, stabilisce che qualsiasi insieme può essere ben ordinato. Si tratta di un assioma sorprendente, indipendente dagli altri assiomi su cui si regge la teoria degli insiemi, e che può assumere forme apparentemente del tutto differenti, ma in realtà equivalenti (vedi paragrafo specifico).

Come si può creare una funzione di scelta (choice function) dato un insieme con WO. [Go 264] Dato un well-order R su M. Allora ogni subset A contiene un elemento minimo. Quindi possiamo definire:

h : P(M)\{ ∅} ➙ M

A ↦ min A

Dimostrazione di come si possa assegnare un cardinale (aleph) ad un insieme X mediante AC sotto forma di choice function. [Go 265] Se prendiamo l'assioma di scelta nella forma che stabilisce l'esistenza di una choice function h : P(X)\∅ ➙ X con h(A) ∈ A per ogni A ⊆ X e un insieme c non appartenente ad X, possiamo provare che esiste una bijezione tra X e un ordinale nel seguente modo. Prendiamo un ordinale α tale che α ⋠ X (l'esistenza di tale ordinale è garantita dal teorema di Hartog). Utilizzando h definiamo una funzione suriettiva α ➙ X ∪ c:

f : α ➙ X ∪ c

0 ↦ h(X)

β ↦ h(X\Range(f|_β)) se X\Range(f|_β) ≠ ∅

β ↦ c se X\Range(f|_β) = ∅

Si può mostrare che se f(γ) e f(λ) sono in X (cioè non hanno immagine c) allora è f(γ) ≠ f(λ)

Si può mostrare che, dato Hartog e l'affermazione immediatamente precedente, c deve essere in Range(f), cioè che ci deve essere una "eccedenza" di α su X, e quindi l'insieme delle controimmagini di c non sia vuoto.

Sia δ il least element delle controimmagini di c

Si può mostrare che f|_δ è una bijezione δ ➙ X

Si può sfruttare questa bijezione per dotare X di un well-order

Dimostrazione alternativa di come si possa assegnare un cardinale (aleph) ad un insieme X mediante AC sotto forma di choice function. Il teorema di Hartog stabilisce che, dato un insieme X, esiste un ordinale α tale che α⋠ X. Senza l'assioma di scelta, utilizzando l'assioma dell'unione, l'assioma di separazione, l'assioma delle coppie e il buon ordinamento di α riusciamo a costruire una serie di funzioni X ➙ α ciascuna delle quali manda tutti gli elementi di X in un solo elemento di α. Se postuliamo l'esistenza di una choice function, possiamo selezionare, per ciascuna di queste funzioni, un elemento dalla controimmagine e combinare tali coppie. Possiamo usare la tecnica con cui sopra abbiamo usato la funzione f e un elemento estraneo c per creare una funzione suriettiva α ➙ X ∪ c. A questo punto si possono avere tre possibilità: o gli elementi di X terminano prima di quelli di α o gli elementi di α terminano prima di quelli di X oppure terminano nello stesso momento (i due insiemi sono equinumerosi). Le ultime due possibilità, per Hartog, non possono essere, quindi deve essere la prima. Se gli elementi di X terminano prima di quelli di α, avremo una funzione suriettiva α ➙ X ∪ c. A questo punto si prosegue con la dimostrazione di Goldrei p. 265

La dimostrazione di come si possa assegnare un cardinale (aleph) ad un insieme X mediante AC sotto forma di WO si riconduce a quella, data sopra, di come a un insieme ben ordinato possa essere assegnato un cardinale.

Molti altri risultati della teoria di Cantor, scoprirono i matematici, dipendono in modo vitale da tale assioma. Come abbiamo detto più sopra, riferendo dei risultati di Gödel e di Cohen, l'assioma di scelta, esattamente come la congettura GCH è indipendente dagli assiomi di ZF.

il buon ordine dei cardinali

back to index

▸ Ordine basato su ≼ (Enderton) (Lolli)

[En 145] Dati due numeri cardinali κ, λ e due insiemi K,L tale che card(K) = κ e card(L) = λ, stabiliamo che κ ≤ λ se e solo se K ≼ L

[En 146] Definiamo poi κ < λ sse k ≤ λ e κ ≠ λ

[En 146] Si può provare che l'ordine ≤ è:

▸ riflessivo: κ ≤ κ

▸ transitivo: κ ≤ λ ≤ μ ➙ κ ≤ μ

▸ antisimmetrico: κ ≤ λ & λ ≤ κ ➙ κ = λ

▸ lineare: κ ≤ λ oppure λ ≤ κ

▸ Ordine basato sulla relazione di appartenenza (Enderton)

I numeri cardinali, come qualsiasi altro numero ordinale, sono ben-ordinati dalla relazione di appartenenza. Posto questo, è facile verificare che questo ordine coincide con l'ordine basato su ≼

▸ L'ordine basato su ∈ coincide con quello basato su ≼ (Lolli) (Enderton)

[Lo 158] [En 199] Lolli ed Enderton dimostrano che la relazione di appartenenza tra i numeri cardinali (cioè gli ordinali più piccoli tra quelli equinumerosi) coincide con la relazione basata su ≼:

A ≈ B ⇔ card(A) = card(B)

A ≺ B ⇔ card(A) ∈ card(B)

Scriveremo "≤" e "<" per le relazioni di ordine e ordine stretto tra cardinali, anche se questa coincide con la relazione di appartenenza, per comodità di scrittura nel caso "≤"

aritmetica dei cardinali

back to index

[En 139] La definizione delle operazioni tra cardinali è differente da quella delle operazioni tra ordinali:

Addizione tra cardinali:

κ + λ = card(K ∪ L)

dove "card( )" indica la cardinalità dell'insieme tra le parentesi, e K e L sono due qualsiasi insiemi disgiunti di cardinalità κ e λ rispettivamente.

Moltiplicazione tra cardinali:

κ ⋅ λ = card(K x L)

dove K e L sono due qualsiasi insiemi disgiunti di cardinalità κ e λ rispettivamente.

Elevamento a potenza:

κ^λ = card(^LK)

dove ^LK è l'insieme delle funzioni da L in K mentre K ed L sono due qualsiasi insiemi disgiunti di cardinalità κ e λ rispettivamente.

Diseguaglianza:

[En 146] card(K) < card(L) ≡ K ≼ L e K ≉ L

[En 146] k ≤ λ ≡ k < λ oppure k = λ

[Go 269] k < λ è l'usuale relazione di appartenenza

[Go 269] k ≤ λ è il weak order associato

[En 164] L'aritmetica dei cardinali infiniti è parzialmente differente da quella degli ordinali infiniti. Ad esempio, nel caso dei cardinali, si può dimostrare che, se α o β sono infiniti e diversi da zero, si ha:

α + β = α ⋅ β = max(α, β)

ciò che non è vero per tutti gli ordinali. Infatti, come abbiamo visto, 2 ⋅ ω è un ordinale maggiore di ω.

[Go 273] k < 2^k per tutti i cardinali k

[En 146] 0 ≤ k per qualsiasi cardinale k

k ≤ λ ≤ μ ⇒ k ≤ μ

k ≤ λ e λ ≤ μ ⇒ k = λ

k ≤ λ oppure λ ≤ k

[En 148] k ≤ λ < μ ⇒ k < μ

k < λ ≤ μ ⇒ k < μ

[En 149] 2^ℵ⁰ ⋅ 2^ℵ⁰ = 2^ℵ⁰^⋅^ℵ⁰ = 2^ℵ⁰

[En 162] per ogni cardinale infinito k si ha che k ⋅ k = k

[Go 271] α ⋅ β = β ⋅ α

[Go 272] k + λ = λ + k

k + (λ + μ) = (k + λ) + μ

k ⋅ (λ ⋅ μ) = (k ⋅ λ) ⋅ μ

k ⋅ (λ + μ) = (k ⋅ λ) + (k ⋅ μ)

k^λ⁺^μ = k^λ ⋅ k^μ

k^λ^⋅^μ = (k^λ)^μ

[Go 272] dati k ≤ λ (dove ≤ è l'ordine dei cardinali "appartiene o è eguale") si ha:

k + μ ≤ λ + μ

k ⋅ μ ≤ λ ⋅ μ

k^μ ≤ λ^μ

μ^k ≤ μ^λ

[Go 272] 2^k + k = 2^k

2^k ⋅ 2^λ = 2^{max(k ,
λ)}

Se k ≤ λ allora k^λ ≤ 2^λ

Come possono essere due ordinali equinumerosi e contemporaneamente ordinati da ∈

Il fatto che due ordinali possano essere equinumerosi e contemporaneamente ordinati dalla relazione ∈ può apparire sorprendente. Si tenga presente che questo non è possibile per gli ordinali finiti, ma solo per gli ordinali infiniti. Poiché ogni ordinale è un insieme transitivo, e cioè un insieme α tale che β ∈ α ➙ β ⊆ α, dati due ordinali, uno è, non solo un elemento, ma anche un sottoinsieme proprio dell'altro. Esistono facili esempi di insiemi infiniti equinumerosi rispetto ad un sottoinsieme proprio: ad es. R ≈ (0,1). Ma si potrebbe obiettare che non si tratta di ordinali. Consideriamo allora la serie di ordinali: ω, ω⁺, ω⁺⁺, …, che sono in realtà equinumerosi. Come si sa, ω = {1, 2, 3, …} e ω⁺ = ω ∪ {ω} = {1, 2, 3, .., ω}. Tra ω ed ω⁺ si può stabilire una bijezione collegando 1 a ω e la successione 2, 3, … di ω e alla successione 1, 2, 3, … di ω⁺.

Il problema non è solo il fatto che due ordinali equinumerosi dovrebbero avere due ordini diversi. Esempi di due insiemi equinumerosi con ordini diversi sono facili da trovare. Il fatto è che gli ordinali sono uno sottoinsieme proprio di un altro.

gli aleph

la successione degli aleph. l'indicizzazione mediante ordinali.

back to index

Ora si presentava per i cardinali un problema simile a quello della successione degli ordinali: come definire un ordine e una successione che li comprendessero tutti e li ordinasse in base alla grandezza? Cantor utilizzò gli ordinali per indicizzare i cardinali, creando la successione degli aleph.

Poter utilizzare nella definizione del cardinale successore una caratteristica dell'ordinale indice (quella di essere un ordinale limite) consente di raggiungere il risultato desiderato: definire una successione che comprende tutti i cardinali in ordine di grandezza.

La successione dei numeri cardinali inizia con l'insieme vuoto: ∅, lo zero. Prosegue con i numeri naturali: 1, 2, 3, ... Poi vengono i numeri infiniti, che Cantor chiamò aleph, dal nome della prima lettera dell'alfabeto ebraico, che si scrive "ℵ". Come già detto, gli aleph sono gli ordinali iniziali e costituiscono i cardinali infiniti.

La successione degli aleph è definita ricorsivamente:

ℵ(0) = ω : Omega, il più piccolo degli infiniti

ℵ(γ⁺) : Aleph successore, il più piccolo ordinale iniziale α tale che ℵ(γ) possa applicarsi su α ma non sia ad esso equipotente.

ℵ(λ) = ∪{ℵ(γ) : γ ∈ λ} : Aleph limite, l'unione di tutti gli aleph contrassegnati da un qualsiasi ordinale γ contenuto nell'ordinale limite λ

(γ⁺ indica l'ordinale successore di γ, e ℵ(γ) ≺ α significa che ℵ(γ) può essere proiettato iniettivamente su α, ma non bijettivamente)

(Le espressioni "aleph successore" e "aleph limite" non si trovano nei testi, ma solo perché i matematici preferiscono le espressioni equivalenti di "cardinale successore" e "cardinale limite").

Come si è già detto, per ogni cardinale infinito, a cominciare da omega, esistono infiniti ordini diversi, ciascuno dei quali è esemplificato da un ordinale che è equipotente a quel cardinale.

Ordinali infiniti e cardinali infiniti (aleph) costituiscono i numeri infiniti, contrapposti ai numeri finiti dell'aritmetica ordinaria.

Cantor aveva scoperto, accanto ai numeri cardinali, già noti ai matematici, un insieme immensamente più grande e complesso, quello dei numeri ordinali.

Con i cardinali e gli ordinali aveva ottenuto due tipi di numeri, con proprietà matematiche molto diverse.

i paradossi dell'insieme di tutti i cardinali e dell'insieme di tutti gli ordinali.

back to index

L'insieme di tutti gli aleph – dei cardinali infiniti – non esiste, né esiste l'insieme degli ordinali infiniti: sono costituiti da quelle che i logici chiamano classi proprie, la cui qualificazione come insiemi genera inesorabilmente paradossi.

Ne saranno indicati qui due: il paradosso della definizione dell'insieme di tutti gli ordinali o paradosso di Burali-Forti (dal nome del matematico italiano che lo segnalò nel 1897), e il paradosso della cardinalità dell'insieme degli ordinali ([Go 269] c.d. paradosso di Cantor, rivelato da Cantor nel 1899).

Per quanto riguarda il primo, chiediamoci se la classe di tutti i numeri ordinali è esso stesso un ordinale. Sembrerebbe di sì, perché soddisfa la definizione di insieme transitivo ed è ben ordinato dalla relazione di appartenenza. Ma contemporaneamente non può essere un ordinale, perché dagli stessi assiomi della teoria degli insiemi che consentono di definire compiutamente i numeri ordinali, e in particolare dal cosiddetto assioma di regolarità o assioma di fondazione (Fundierungsaxiom), si ricava la conseguenza logica che un ordinale non può appartenere a se stesso.

(L'assioma di regolarità dice che ogni insieme non vuoto A ha almeno un elemento m tale che m ∩ A = ∅).

Per quanto riguarda il secondo paradosso, si pensi a questa contraddizione: qual è la cardinalità della classe di tutti gli aleph? Questa cardinalità, l'aleph degli aleph, non può essere uno degli aleph che include, perché c'è sempre un aleph superiore. Ma contemporaneamente deve essere uno di questi aleph, perché, per definizione, li include tutti. [Kl 117] In due lettere a Dedekind del 28 luglio e del 28 agosto 1899, Cantor si chiese se l'insieme di tutti i numeri cardinali sia esso stesso un insieme perché, se lo fosse, avrebbe dovuto avere un numero cardinale maggiore di ogni altro numero cardinale. Egli pensava di dover rispondere in senso negativo distinguendo tra insiemi coerenti e insiemi non coerenti.

l'ipotesi del continuo ch e l'ipotesi generalizzata del continuo gch

back to index

Esistono altri infiniti, di cardinalità superiore a quella dei numeri reali?

P(A)

P(P(A))

P(P(P(A)))

……………

Ogni volta si ottiene un infinito di dimensione superiore.

Nel 1940 Kurt Gödel provò che se ZF è coerente, lo è pure ZF con CH e GCH.