I MOLTIPLICATORI DI LAGRANGE

I MOLTIPLICATORI DI LAGRANGE

nozioni generali

▸ Le funzioni Rⁿ ➙ R^m tra spazi euclidei sono un sottogruppo delle funzioni tra spazi vettoriali qualsiasi di dimensione qualsiasi.

Quando n = m = 1 una tale funzione è detta funzione a valori reali di una variabile reale.

Quando n = 1 e m > 1 è detta funzione a valori vettoriali di una variabile reale

Quando n > 1 e m = 1 è detta funzione a valori reali di variabile vettoriale, o semplicemente campo scalare

Quando n > 1 e m > 1 è detta funzione a valori vettoriali di una variabile vettoriale, o semplicemente campo vettoriale

Queste ultime funzioni possono essere scomposte nelle cosiddette funzioni componenti:

f₁ : Rⁿ ➙ R

…………..

f_m : Rⁿ ➙ R

tali che si abbia:

f(x₁, …, x_n) = (f₁(x₁, …, x_n), …, f_m(x₁, …, x_n))

Per evitare ingombranti denominazioni, nel prosieguo parleremo rispettivamente di funzioni R ➙ R, funzioni R ➙ R^m, funzioni Rⁿ ➙ R e funzioni Rⁿ ➙ R^m anche se tecnicamente esse potrebbero essere definite solo su un sottoinsieme dello spazio euclideo indicato come dominio.

▸ Un sottospazio S dello spazio vettoriale V è un sottoinsieme che è esso stesso uno spazio vettoriale con le stesse operazioni definite in V. Per essere un sottospazio, deve essere chiuso rispetto a tali operazioni, cioè dati i vettori s₁, s₂ e lo scalare k, la somma s₁ + s₂ e il prodotto k ⋅ s₁ devono appartenere anch’essi ad S. In questo modo vengono ereditate tutte le altre proprietà di spazio vettoriale.

▸ Data una funzione di classe C¹ g : Rⁿ ➙ R^m (m < n) e un punto p in cui g(p) = 0 e il rango della matrice

è pari ad m, allora esiste un intorno U di p con una permutazione delle coordinate, esiste un aperto V ⊂ R^n–m costituito dalla proiezione (p_i1 . …, p_in) ↦ (p_i1, …, p_in–m) delle coordinate permutate di U∩g^–1(0), esiste una funzione h : V ➙ R^m tali che ogni punto di U∩g^–1(0) abbia coordinate (p_i1, …, p_in–m, h(p_i1, …, p_in–m))

Ma, riguardo l’insieme U∩g^–1(0), questa è anche la definizione di varietà (n – m)-dimensionale, cosicché U∩g^–1(0) è una varietà (n – m)-dimensionale.

▸ Data una funzione f : Rⁿ ➙ R il gradiente nel punto a è dato da

Abbiamo la seguente relazione tra vettore gradiente e derivata direzionale:

D_vf(a) = ∇f(a) ⋅ v

superfici k-dimensionali

Le funzioni g_i che costituiscono il vincolo possono essere di numero qualsiasi, purché inferiore alla dimensione dello spazio su cui è definita la funzione f da massimizzare.

Così, nel caso che la funzione f sia definita su R³ possiamo avere una sola funzione vincolo o due funzioni g₁, g₂, che costituiscono le funzioni componenti di un’unica funzione G : R³ ➙ R²

Nel caso di una sola funzione continuamente differenziabile g, l’insieme di livello corrispondente ai punti nei quali si ha g = 0 e rango della jacobiana eguale ad uno costituisce una familiare superficie definita in forma parametrica.

La definizione classica di rappresentazione parametrica regolare di classe C^k di una superficie in R³ è quella di una funzione C^k φ : U ⊂ R² ➙ R³:

x₁ = φ₁(u,v)

x₂ = φ₂(u,v)

x₃ = φ₃(u,v)

definita su un aperto U di R², con la jacobiana di rango 2.

Richiedere che la jacobiana della superficie abbia rango 2 equivale a richiedere che i due vettori ∂φ/∂u e ∂φ/∂v siano linearmente indipendenti

Questi due vettori individuano un piano. E’ facile dimostrare che tale piano contiene tutti i vettori tangenti alle curve differenziabili giacenti sulla superficie e passanti per il punto considerato.

Si dice che la superficie è semplice se l’applicazione φ è iniettiva

Per dimostrare che la jacobiana di φ è di rango 2 si ricorre al teorema della funzione implicita.

Il teorema della funzione implicita stabilisce che, laddove la jacobiana della funzione continuamente differenziabile g abbia rango uno in un punto p, allora esiste un intorno U di p in R³ che racchiude una porzione g^–1(0)∩U dell’insieme di livello costituito da tutti i punti p tali che g(p) = 0 e una funzione h : R² ➙ R che manda due delle coordinate dell’insieme di livello nella terza coordinata in modo che sia g(x_i1,x_i2,h(x_i1,x_i2)) = 0

Il che vuol dire che nell’intorno U la superficie di livello può essere espressa mediante due parametri x_i1 e x_i2:

x_i1 = x_i1

x_i2 = x_i2

x_i3 = h(x_i1,x_i2)

Si può facilmente calcolare che la jacobiana della parametrizzazione ottenuta con il teorema della funzione implicita è:

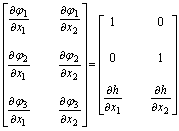
Questa matrice ha chiaramente rango 2, perché le due prime righe sono linearmente indipendenti

La condizione che la jacobiana della rappresentazione parametrica regolare abbia rango 2 assicura che ogni punto della immagine abbia un piano tangente, formato dalle derivate di tutte le curve passanti per il punto considerato.

Assicura anche che si tratti di una superficie “liscia”, senza spigoli o cuspidi, perché si può dimostrare che laddove l’immagine di una funzione differenziabile φ : R² ➙ R³ ha uno spigolo o una cuspide, allora le derivate parziali ∂φ/∂u e ∂φ/∂v devono essere tutte zero. Ne consegue che se la matrice jacobiana ha invece rango 2 allora si tratta di una superficie senza spigoli o cuspidi.

La particolare rappresentazione parametrica regolare assicurata dal teorema della funzione implicita è nota come rappresentazione di Monge: la sua peculiarità sta nel fatto che i due parametri coincidono con due delle variabili in R³.

x₁ = u

x₂ = v

x₃ = φ(u,v)

Il tipo più semplice di rappresentazione di Monge si ha quando la terza coordinata è quella del punto dell’insieme di livello di coordinate (x₁, x₂, x₃).

La rappresentazione di Monge ha come caratteristiche aggiuntive quella di essere iniettiva e bicontinua.

Se le funzioni vincolo sono due, g₁, g₂, che costituiscono le funzioni componenti di un’unica funzione G : R³ ➙ R² allora l’insieme di livello G^-1(0) sarà non una superficie ma una linea.

Anche in questo caso il teorema della funzione implicita, nell’intorno di ciascun punto p nel quale la jacobiana delle derivate ∂g_i/∂x_i ha rango 2 dimostra l’esistenza di una parametrizzazione del tipo:

x_i1 = x_i1

x_i2 = h₁(x_i1)

x_i3 = h₂(x_i1)

Ecco due esempi di insiemi di livello che, non avendo la jacobiana delle derivate di rango 2, non rappresentano una linea, bensì un punto o una croce.

▸ S = {(x,y) | x² + y² = 0} è soddisfatto solo nell’origine, e consiste quindi di un solo punto; ∇g(0) = (2x , 2y) = (0 , 0) e si vede come S non è l’immagine di una curva in un intorno del punto (0,0)

▸ S = {(x,y) | x² – y² = 0} è costituito dalle due bisettrici degli assi coordinati, ∇g(0) = (2x , – 2y) = (0,0) e si vede come S non è una immagine di una curva, avendo forma di croce.

Una rappresentazione parametrica regolare iniettiva e bicontinua (omeomorfa) rappresenta l’inversa di una carta locale con cui la geometria differenziale moderna definisce le varietà o manifolds. Se ogni punto della superficie ha una siffatta carta locale, allora in luogo di superficie, si usa il termine più astratto di varietà k-dimensionale o k-varietà, che può essere applicato a curve, superfici e ad altri insiemi di punti parametrizzati con più di due parametri.

Nella teoria delle varietà o manifolds una parametrizzazione Rⁿ ➙ R^N corrisponde al concetto di immersione non iniettiva (funzione con la jacobiana di rango pari a quello del dominio)

Il caso di parametrizzazione di Monge collegata dal teorema della funzione implicita ad un insieme di livello, corrisponde invece al concetto di immersione regolare (funzione iniettiva, con jacobiana di rango pari a quello del dominio e omeomorfa sulla propria immagine dotata della topologia indotta dal codominio).

varietà k-dimensionali corrispondenti a k funzioni vincolo

Quando le funzioni vincolo g_i sono in numero k con k > 2, non più su R³ ma su R^N con N qualsiasi, l’insieme di livello G = 0 (G è la funzione le cui funzioni componenti sono le g_i) è un oggetto geometrico più astratto di una superficie, che prende il nome di varietà k-dimensionale.

Daremo qui di seguito la definizione di varietà k-dimensionale o k-varietà che generalizza il concetto di superficie o varietà 2-dimensionale.

S ⊂ Rⁿ è un k-dimensional patch se esiste una permutazione x_i1, …, x_in delle coordinate dei punti di S e una funzione differenziabile h : U ⊂ R^k ➙ R^n–k tale che nel nuovo sistema di coordinate le coordinate dei punti di S siano date da (x_i1, …, x_ik, h (x_i1, …, x_ik))

Un insieme M ⊂ Rⁿ è chiamato una varietà k-dimensionale in Rⁿ se ogni punto di M si trova in un aperto V ⊂ Rⁿ tale che V ∩ M è un k-dimensional patch.

Si può dimostrare che una varietà k-dimensionale ha un piano tangente k-dimensionale in ognuno dei suoi punti

Si può dimostrare che l’insieme di livello di cui sopra, se la jacobiana di G ha rango k, è una varietà k-dimensionale, e come tale ha un piano tangente k-dimensionale in ognuno dei suoi punti.

massimi, minimi, punti stazionari

▹ Se p è un punto di massimo per f in un aperto, allora il gradiente ∇f è ortogonale al vettore velocità di qualsiasi curva che passi per p

Questo teorema è applicabile sia al boundary (cioè ai punti dell’insieme S in ogni intorno dei quali cade sia un punto interno all’insieme che un punto esterno all’insieme) che all’interior di S (cioè ai punti dell’insieme s per i quali esiste un intorno nel quale cadono solo punti di S) e per l’interior dà come risultato che p deve essere un punto critico.

▸ Quando tutte le componenti del gradiente ∇f di una funzione differenziabile f : Rⁿ ➙ R sono nulle in un punto p, cioè se ∇f = 0, allora tale punto dicesi punto stazionario o punto critico della funzione

I punti stazionari di una funzione si classificano generalmente in tre categorie: punti di massimo, punti di minimo e punti di sella.

Si dice che una funzione Rⁿ ➙ R ha un massimo assoluto in un punto a di un sottoinsieme S di Rⁿ se

f(x) ≤ f(a)

per ogni x in S. Il valore f(a) è detto massimo assoluto di f in S.

Si dice che una funzione ha un massimo relativo in a se la disuguaglianza f(x) ≤ f(a) è soddisfatta per tutti gli x di un intorno di a contenuto in S.

In modo analogo si definiscono il minimo assoluto in un punto di S e il minimo relativo in un punto di S.

Si dice estremo di f un numero che sia o un massimo relativo o un minimo relativo di f.

Un punto è detto punto di sella se ogni intorno di a contiene punti x tali che f(x) <f(a) e altri punti tali che f(x) > f(a)

▸ Se f ha un estremo in un punto interno p del sottoinsieme S ed è ivi differenziabile, allora tutte le derivate parziali del primo ordine sono nulle (il vettore gradiente è eguale a zero).

Questa è però solo una condizione necessaria ma non sufficiente (in altre parole, non è vero l’inverso: se p è un punto critico non necessariamente la funzione ha un massimo o minimo locale in quel punto).

▹ Se f : Rⁿ ➙ R possiede un massimo/minimo su una superficie n-dimensionale, non necessariamente il gradiente è eguale a zero

Se invece f : Rⁿ ➙ R possiede un massimo o minimo su una superficie n-dimensionale, non necessariamente il suo gradiente in tal punto è eguale a zero (cioè è un punto critico della funzione).

Pertanto, nel caso di una funzione definita su un sottoinsieme di Rⁿ compreso entro una superficie (n – 1)-dimensionale chiusa, per trovare i punti di massimo o minimo locali occorre usare procedimenti diversi a seconda che tali punti si trovino sulla superficie o all’interno di essa: nel secondo caso si procede eguagliando a zero le derivate prime e, una volta trovati i punti, si procede a determinare se siano di massimo, minimo o di sella tramite l’analisi della matrice hessiana delle derivate seconde; nel primo caso si procede col metodo dei moltiplicatori di Lagrange.

▹ [0901061522] Dato un insieme compatto (chiuso e limitato) una funzione ha su di esso un massimo e un minimo, che possono essere nell’interior o nel boundary. Tra i casi più interessanti vi sono quelli di regioni entro (iper)superfici chiuse.

Una funzione f : D ⊂ Rⁿ ➙ R su un subset D compatto (= chiuso e limitato), se continua ha un massimo e un minimo su D.

Frequentemente si considerano i punti entro una superficie (n – 1)-dimensionale: regioni racchiuse da una curva chiusa in R²; regioni racchiuse da una superficie chiusa in R³; e così via. La funzione può avere un massimo/minimo sia all’interno di D sia sulla (n – 1)-superficie. Se il punto di massimo/minimo si trova all’interno di D deve essere un punto critico e viene individuato ponendo le derivate parziali eguali a zero. Ma se è un punto di confine (in ogni intorno vi sono sia punti che appartengono a D sia punti che non appartengono a D) allora non è necessariamente un punto critico e per individuarlo si deve usare il procedimento dei moltiplicatori di Lagrange.

Se una funzione f : Rⁿ ➙ R ha un massimo o minimo locale su un aperto di Rⁿ allora il punto è un punto critico.

▹ Un teorema analogo a quello [0901061522] degli estremi su un intervallo chiuso e limitato di Rⁿ si ha per funzioni Rⁿ ➙ R continue su un intervallo chiuso. In tal caso infatti la chiusura più la continuità implicano la limitatezza e quindi la esistenza di un estremo superiore e inferiore dei valori della funzione.

il metodo dei moltiplicatori di lagrange

▹ Il metodo dei moltiplicatori di Lagrange per trovare i possibili punti di massimo/minimo di una funzione Rⁿ ➙ R sull’insieme di livello di una funzione Rⁿ ➙ R^m

Data una funzione di classe C¹ g : Rⁿ ➙ R^m consideriamone l’insieme di livello g^–1(0) dei punti le cui coordinate soddisfano le equazioni:

g₁(x₁, …, x_n) = 0

…………………

g_m(x₁, …, x_n) = 0

Se la funzione differenziabile f : Rⁿ ➙ R ha un massimo o minimo in un punto p di tale insieme di livello, allora esistono m numeri reali λ₁, …, λ_m (chiamati moltiplicatori di Lagrange) tali che si ha:

∇f(a) = λ₁∇G₁(a) + … + λ_m∇G_m(a)

Per determinare il valore di x₁, …, x_n e di λ₁, …, λ_m si utilizza il sistema di n + m equazioni:

∇f(x) = λ₁∇G₁(a) + … + λ_m∇G_m(a)

g₁(x) = 0

…………………

g_m(x) = 0

Dato che è:

le equazioni sono:

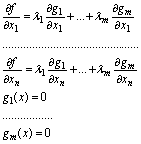
Il metodo è valido se il numero dei vincoli, m, è più piccolo del numero delle variabili, n, e se i determinanti jacobiani delle funzioni vincolo rispetto a m delle n variabili x₁,…,x_n non sono tutti nulli nei punti di estremo in questione.

Quest’ultimo requisito equivale a chiedere che il rango della jacobiana sia m nel punto considerato, ovvero anche a chiedere che i gradienti delle m funzioni vincolo siano linearmente indipendenti.

derivata direzionale iterata di ordine k che approssima una funzione rⁿ ➙ r^m nel punto a + h con h vettore di rⁿ.

▸ La derivata direzionale di una derivata direzionale di ordine n di una funzione f : Rⁿ ➙ R rispetto al vettore (h₁, …, h_n) è data da:

D_hD₁^j1…D_n^jnf = ∑₁_≤_r_≤_n h_rD₁^j1…D_r^jr+1…D_n^jnf

▸ La derivata direzionale iterata nella direzione del vettore (h₁, …, h_n) è data da:

D_h^kf = (h₁D₁ + … + h_nD_n)^kf

cioè:

dove è:

Questa formula è la formula multinomiale, che dà i coefficienti della potenza (x₁ + … + x_n)^k, mentre la formula del binomio, o, espresso con la simbologia di Edwards , che si identifica col triangolo di Tartaglia, fornisce i coefficienti della potenza (x₁ + x₂)^k.

Il coefficiente binomiale (^k_n) rappresenta le combinazioni distinte, senza ripetizioni, senza considerare l’ordine, di n elementi scelti da un insieme di k elementi.

Il coefficiente multinomiale (^k_j1,…,jn) indica in quanti modi distinti (senza considerare l’ordine) possono essere scelti n gruppi di oggetti, rispettivamente di j₁,…,j_n elementi su un totale di k oggetti.

polinomio di taylor di ordine k di una funzione rⁿ ➙ r di classe c^k

L’espansione di Taylor della funzione f : Rⁿ ➙ R di classe C^k è:

con:

dove é

D_h⁰f(a) = f(a).

Se scriviamo x = a + h otteniamo:

f(x) = P_k(x – a) + R_k(x – a)

dove P_k(x – a) è un polinomio di grado k^th nei componenti x₁ – a₁, …, x_n – a_n e

esempio di polinomio di taylor di ordine 3 che approssima il valore di una funzione r³ ➙ r

Data f : R³ ➙ R, scriviamo:

f(x) = f(a) + D_h¹f(a) + (1/2!) D_h²f(a) + (1/3!) D_h³f(a)

= f(a) + [h₁D₁f + h₁D₃f + h₃D₃f] + (1/2!) D_hf[h₁D₁f + h₁D₃f + h₃D₃f] + (1/3!) D_hf{ D_hf[h₁D₁f + h₁D₃f + h₃D₃f] }

Senza occuparci ulteriormente della formula sviluppiamo D_hf[h₁D₁f + h₁D₃f + h₃D₃f]:

D_hf[h₁D₁f + h₁D₃f + h₃D₃f] =

= D₁D₁h₁h₁ + D₁D₂h₁h₂ + D₁D₃h₁h₃ + D₁D₂h₁h₂ + D₂D₂h₂h₂ + D₂D₃h₂h₃ + D₁D₃h₁h₃ + D₂D₃h₂h₃ + D₁³h³ =

= D₁² h₁² + 2D₁D₂h₁h₂ + 2D₁D₃h₁h₃ + D₂²h₂² + 2D₂D₃h₂h₃ + 2D₃²h₃²

Sviluppiamo ora D_hf{ D_hf[h₁D₁f + h₁D₃f + h₃D₃f] }:

D_hf{ D_hf[h₁D₁f + h₁D₃f + h₃D₃f] } =

= D_hf{ D₁² h₁² + 2D₁D₂h₁h₂ + 2D₁D₃h₁h₃ + D₂²h₂² + 2D₂D₃h₂h₃ + 2D₃²h₃² }

= D₁³h₁³ + 2D₁²D₂h₁²h₂ + 2D₁²D₃h₁²h₃ + D₁D₂²h₁h₂² + 2D₁D₂D₃h₁h₂h₃ + D₁D₃²h₁h₃² + D₁²D₂h₁²h₂ + 2D₁D₂²h₁h₂² + 2D₁D₂D₃h₁h₂h₃ + D₂³h₂³ + 2D₂²D₃h₂²h₃ + D₂D₃²h₂h₃² + D₁²D₃h₁²h₃ + 2D₁D₂D₃h₁h₂h₃ + 2D₁D₃²h₁h₃² + D₂²D₃h₂²h₃ + 2D₂D₃²h₂h₃² + D₃³h₃³ =

= D₁³h₁³ + 3D₁²D₂h₁²h₂ + 3D₁²D₃h₁²h₃ + 3D₁D₂²h₁h₂² + 6D₁D₂D₃h₁h₂h₃ + 3D₁D₃²h₁h₃² + D₂³h₂³ + 3D₂²D₃h₂²h₃ + 3D₂D₃²h₂h₃² + D₃³h₃³

Utilizzando la regola del coefficiente multinomiale i coefficienti sono rispettivamente:

D₁³h₁³ + D₁²D₂h₁²h₂ + D₁²D₃h₁²h₃ + D₁D₂²h₁h₂² + D₁D₂D₃h₁h₂h₃ + D₁D₃²h₁h₃² + D₂³h₂³ + D₂²D₃h₂²h₃ + D₂D₃²h₂h₃² + D₃³h₃³

e cioè:

Come si vede, tali coefficienti coincidono con quelli trovati col calcolo diretto.

Si è visto sopra che a questi coefficienti occorre ulteriormente moltiplicare 1/k! dove k è il grado della derivata.

il metodo dell’hessiana

▸ Dato un punto critico a di una funzione f : Rⁿ ➙ R di classe almeno C³, allora possiamo scrivere (espansione di Taylor):

f(a + h) – f(a) = q(h) + R₂(h)

dove:

q(h) = ½D_h²f(a) = ½(h₁D₁ + … + h_nD_n)²f(a) = ½∑_≤_i,j_≤_n D_iD_jf(a)x_ix_j = x^t A x

dove le entrate a_ij della matrice A sono date da a_ij = ½D_iD_jf(a) e la matrice A è simmetrica, dato che è D_iD_jf(a) = D_jD_if(a).

Quanto al resto si ha:

Se non tutte le derivate seconde svaniscono allora q(h) è un polinomio di secondo grado nelle incognite h₁, …, h_n di forma:

q(h) = ∑₁_≤_i_≤_j_≤_n a_ijh_ih_j

ed è chiamato forma quadratica di una funzione in un punto critico a.

Possiamo scrivere:

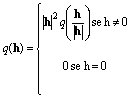
Dal momento che h/|h| è un punto sulla sfera unitaria S^n–1, ne segue che la forma quadratica è completamente determinata dai suoi valori su S^n–1.

Una forma quadratica è chiamata positiva definita (risp. negativa definita) se e solo se è positiva (risp. negativa) in ogni punto di S^n–1 (e dunque ovunque eccetto che nel punto zero), e è chiamata non definita se assume sia valori positivi che valori negativi su S^n–1 (e dunque in ogni intorno dello zero).

Si noti che y², visto come una forma quadratica in x ed y in cui i coefficienti di x² e xy sono zero, non è né positiva definita né negativa definita né non definita (è non negativa dappertutto ma è zero sull’asse x)

▸ [0901051914] (7.5) Data una funzione f : Rⁿ ➙ R di classe C³ nell’intorno di un punto critico a, allora in tale punto essa ha:

▸ un minimo locale se la sua forma quadratica q(h) è positiva definita

▸ un massimo locale se la sua forma quadratica è negativa definita

▸ né un minimo né un massimo se q(h) è non definita

Se q(h) = 0 il teorema non si applica

Questo teorema si basa sul fatto che, poiché le derivate prime sono zero, la formula di Taylor di secondo grado assume la forma:

dove E(a,h) ➙ 0 se h ➙ 0

E’ abbastanza intuitivo che, essendo il resto ∥h∥² E₂(a,h) un infinitesimo di grado superiore al secondo rispetto ad ∥h∥, per valori piccoli di h esso diventa trascurabile rispetto al valore della forma quadratica, e quindi il valore della differenza f(a + h) – f(a) è completamente determinato dal valore di tale forma quadratica q(h).

▹ [0901061403] Determinazione della natura della forma quadratica q di una funzione f : Rⁿ ➙ R mediante l’analisi degli autovalori della forma lineare associata

Se una forma quadratica ha il minimo/massimo su S^n–1 allora la matrice ha ivi un autovettore v e un autovalore λ, e si ha q(v) = λ

Gli autovalori della forma lineare associata alla forma quadratica sono tutti e soli le soluzioni dell’equazione:

|A – λI = 0

The maximum (minimum) value attained by the quadratic form a(x) = x^t ⋅ A ⋅ x on S^n–1 is the largest (smallest) real root of the equation

|A – λI = 0

▹ [0811231703] Determinazione della natura della forma quadratica q di una funzione f : Rⁿ ➙ R mediante i determinanti dell’hessiana

[0811231703] Un modo alternativo di determinare la natura della forma quadratica q di una funzione f : Rⁿ ➙ R è, anziché tramite l’analisi degli autovalori, mediante i determinanti dell’hessiana.

Consideriamo una forma quadratica q(x) = x^t A x su Rⁿ per la quale | A | ≠ 0. Scriviamo A come (a_ij) e denotiamo con ∆_k il determinante della sottomatrice kxk superiore sinistra della matrice A, cioè:

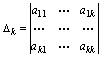
in modo che si ha:

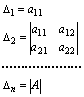
Allora q è:

▸ positiva definita se e solo se ∆_k > 0 per 1 ≤ k ≤ n

▸ negativa definita se e solo se (– 1)^k∆_k > 0 per 1 ≤ k ≤ n

▸ non definita se nessuna delle due precedenti condizioni è soddisfatta

▹ [0901052016] Combinazione della [0901051914] e della [0811231703] e determinazione della natura dei punti stazionari di una funzione f : Rⁿ ➙ R in un punto p (si combinano il teorema [0901051914] sulla forma quadratica in dipendenza dell’hessiana e il teorema [0811231703] sulla natura del punto critico in dipendenza dalla forma quadratica)

Combinando i teoremi [0901051914] e [0811231703] otteniamo il modo di determinare la natura del punto considerato dalla osservazione dell’hessiana.

Occorre innanzitutto che la matrice hessiana (delle derivate seconde) sia nonzero. Data una funzione f : Rⁿ ➙ R di classe C³ nell’intorno di un punto critico a allora si ha:

▸ ∀k ∆_k > 0 ⇒ q positiva definita ⇒ minimo locale

▸ ∀k (– 1)^k∆_k > 0 ⇒ q negativa definita ⇒ massimo locale

▸ nessuna delle condizioni precedenti ⇒ q non definita ⇒ né un massimo né un minimo locale

▹ Il metodo classico di determinazione della natura dei punti critici di una funzione R² ➙ R è una applicazione del teorema [0901052016]

Data una funzione f : R² ➙ R di ordine C² in un intorno del punto critico p. Sia dato:

∆ = D₁²f(a,b)D₂²f(a,b) – (D₁D₂f(a,b))²

Allora:

▸ f ha un minimo locale in p se ∆ > 0 e D₁²f(p) > 0

▸ f ha un massimo locale in p se ∆ > 0 e D₁²f(p) < 0

▸ f non ha né un minimo né un massimo locale in p (ha un punto di sella) se ∆ < 0

▹ Se l’hessiano non è zero e la forma quadratica assume sia valori positivi che negativi allora esistono due distinti sottospazi di Rⁿ ortogonali l’uno all’altro tali che su uno la forma quadratica ha un minimo, e sull’altro la forma quadratica ha un massimo.

Questa è una generalizzazione delle caratteristiche di un punto di sella in R³.

▹ Caso in cui l’hessiano è zero

Se l’hessiano è zero allora tale matrice non fornisce alcuna informazione circa il punto critico. Questa è ad esempio la situazione se la forma quadratica q di f nel punto a è positiva semidefinita ma non positiva definita o negativa semidefinita ma non negativa definita.

Una forma quadratica è detta positiva semidefinita se q(x) ≥ 0 per ogni x e negativa semidefinita se q(x) ≤ 0 per ogni x. Il termine “non definita” significa che q non è né positiva semidefinita né negativa semidefinita (si potrebbe usare il termine “non definita”).

The quadratic form is called positive-semidefinite if q(x) ≥ 0 for all x, and negative-semidefinite if q(x) ≤ 0 for all x. Notice that the terminology “q is nondefinite” which we have been using, actually means that q is neither positive semidefinite nor negative semidefinite (so we might more descriptively have said “non semidefinite”).

il metodo della funzione ausiliaria

▹ Date f : Rⁿ ➙ R e g : Rⁿ ➙ R^m (m < n) consideriamo il set M = g^–1(0) dei punti che hanno gradiente non nullo. Definiamo punto critico a ∈ M quello in cui ∇f è ortogonale allo spazio tangente di M in a. Poiché i vettori gradienti ∇g_i generano il complemento ortogonale a T_a allora si avrà:

∇f(a) = ∑₁_≤_i_≤_mλ_i ∇g_i(a).

Sia a un punto critico per f su M, e denotiamo con q : Rⁿ ➙ R la forma quadratica di f in a e con H la “funzione ausiliaria”:

H = f – ∑₁_≤_i_≤_m λ_ig_i

Si noti che la funzione H è tale che nel punto critico su M si ha:

∇H(a) = ∇f – ∑₁_≤_i_≤_m λ_i∇g_i = 0

cosicché il punto a è un normale punto critico per la funzione H.

Se f e g sono di classe C³ in un intorno di a, allora f ha:

▸ un minimo locale su M in a se q è positiva definita sullo spazio tangente T_a a M in a

▸ un massimo locale su M in a se q è negativa definita sullo spazio tangente T_a a M in a

▸ né un massimo locale né un minimo locale se q è non definita su T_a

La proposizione “q è positiva definita su M” significa che q(x) > 0 per tutti I vettori non zero di T_a

La forma quadratica per H è eguale a ½∑₁_≤_i,j_≤_n D_iD_jH(a)h_ih_j

dimostrazione del teorema:

Consideriamo anzitutto un esempio pratico da tenere presente durante la lettura della dimostrazione

Scriviamo la espansione di Taylor:

H(a + h) = H(a) + 0 + q(h) + R₂(h)

dove lo zero si giustifica col fatto che, trattandosi di un punto critico, tutte le derivate parziali sono zero.

Spostando a secondo membro otteniamo:

H(a + h) – H(a) = q(h) + R₂(h)

Abbiamo anche

H(x) = f(x) se x ∈ M, perché g(x) = 0 per ogni x ∈ M

Occorre mostrare che dato un δ > 0 sufficientemente piccolo si ha:

[0811192043]

Possiamo aggiungere una |h|² al denominatore, perché, essendo una quantità positiva, non altera la condizione:

Poiché è esiste sicuramente un valore δ al disotto del quale e quindi anche se (valore non assoluto) è negativa il segno di dipende solo da

Poiché è , che è il valore della forma quadratica sulla sfera unitaria S^n–1, sia m il valore minimo che f ha su S^n–1∩ T_a; per la condizione in ipotesi si ha m > 0; per la continuità di q è possibile trovare un δ tale che

a + h ∈ M & |h| < δ ⇒ q(h/|h|) > m/2

Con il che si è dimostrata la condizione [0811192043]

esempi (moltiplicatori di lagrange)

▹ [0901061409] Esempio di ricerca di massimo vincolato: due sfere che si intersecano lungo un cerchio obliquo rispetto agli assi con la funzione f data dall’altezza z di ciascun punto di R³.

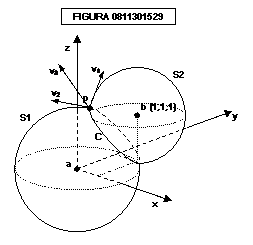
I centri delle sfere S1 ed S2 sono rispettivamente i punti a e b; la sfera S1 ha raggio unitario, mentre la sfera S2 ha raggio = 0,8.

L’equazione di S2 è (1 – x)² + (1 – y)² + (1 – z)² = (0,8)² e il segmento ab misura √1² + 1² + 1² = √3 = 1,732…

Abbiamo le seguenti funzioni:

f : R³ ➙ R : (x_,y, z) ↦ z

g₁ : R³ ➙ R : (x, y, z) ↦ x² + y² + z²

g₂ : R³ ➙ R : (x, y, z) ↦ (1 – x)² + (1 – y)² + (1 – z)²

I vincoli sono:

g₁(x, y, z) = 1

g₂(x, y, z) = 0,8

e la funzione da massimizzare è la f

La funzione f ha evidentemente massimo vincolato nel punto p, dove i gradienti delle funzioni g₁ e g₂ sono rispettivamente v₁ e v₂. Poiché si dimostra che nel punto di massimo vincolato il gradiente ∇f = v₃ è ortogonale a qualsiasi linea che percorra il circolo C, e quindi normale a C, esso è una combinazione lineare dei vettori v₁ e v₂.

▹ [0901061432] Esempio di non-applicabilità del metodo dei moltiplicatori di Lagrange per la determinazione dei minimi/massimi di una funzione f : R³ ➙ R sullo zero set di una funzione g : R³ ➙ R²

I due vincoli, espressi in termini delle due funzioni componenti g₁ e g₂ sono:

z = 0

z² – (y – 1)³ = 0

e cioè:

z = 0

z² – (y³ – 3 y² + 3 y – 1) = 0

e cioè:

z = 0

z² – y³ + 3 y² – 3 y + 1 = 0

Vediamo che z = 0 e y = 1 sono una soluzione della seconda equazione:

– 1³ + 3 ⋅ 1² – 3 ⋅ 1 + 1 = –1 + 3 – 3 + 1 = 0

Il vincolo è quindi costituito in R³ dalla retta z = 0, y = 1

Abbiamo poi:

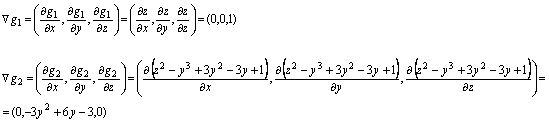
Per quanto riguarda ∇g₂ si vede che nel punto (0,1,0) è:

∇g₂ = (0, – 3 y² + 6y – 3, 0) = (0, – 3 ⋅ 1² + 6 ⋅ 1 – 3, 0) = (0,0,0)

Per quanto riguarda la f abbiamo:

e cioè, poiché x = 0 ed y = 1, abbiamo:

∇f = (0,2,0)

Si vede subito che non esistono costanti λ₁, λ₂ tali che si abbia:

(0,1,0) = λ₁ ⋅ (0,0,1) + λ₂ ⋅ (0,0,0)

e quindi il punto di minima distanza tra la retta e l’asse z, pur esistendo (è il punto (0,1,0)) non può essere calcolato col metodo dei moltiplicatori di Lagrange.

esempi di utilizzo dell’hessiana

▹ [0901061417] Esempio di ricerca degli autovalori della funzione lineare associato alla forma quadratica per stabilire la natura di quest’ultima e conseguentemente la natura di massimo/minimo del punto.

Suppose a is a critical point of the function f : R³ ➙ R and that the quadradic form of f at a is

q(x,y,z) = x² + y² + z² + 4yz

ovvero:

q(x₁,x₂,x₃) = x₁² + x₂² + x₃² + 4x₂x₃

cosicché la matrice di q è:

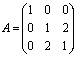
L’equazione caratteristica di A è allora:

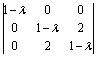= (1 – λ)[(1 – λ)² – 4] = 0

con radici λ = – 1, 1, 3. Come si è detto, il massimo (minimo) valore raggiunto dalla forma quadratica q(x) = x^t A x su X^n–1è la radice reale più grande (più piccola) dell’equazione caratteristica |A – λI| = 0. Il massimo e minimo valore di q su S² sono +3 e – 1 rispettivamente. Dal momento che q ha valori sia positivi che negativi, è non definita. Quindi, per la [0901051914] si ha che f non ha né un minimo né un massimo in a.